算法练习题（涉外黄成老师）

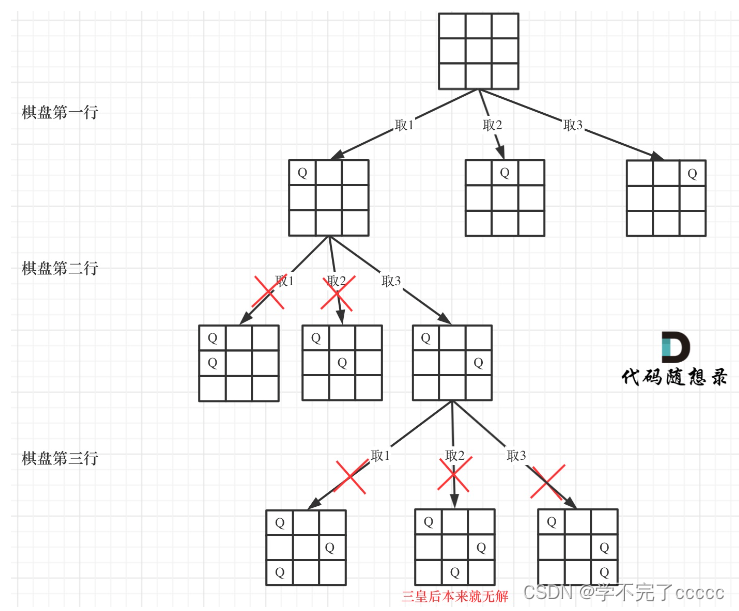
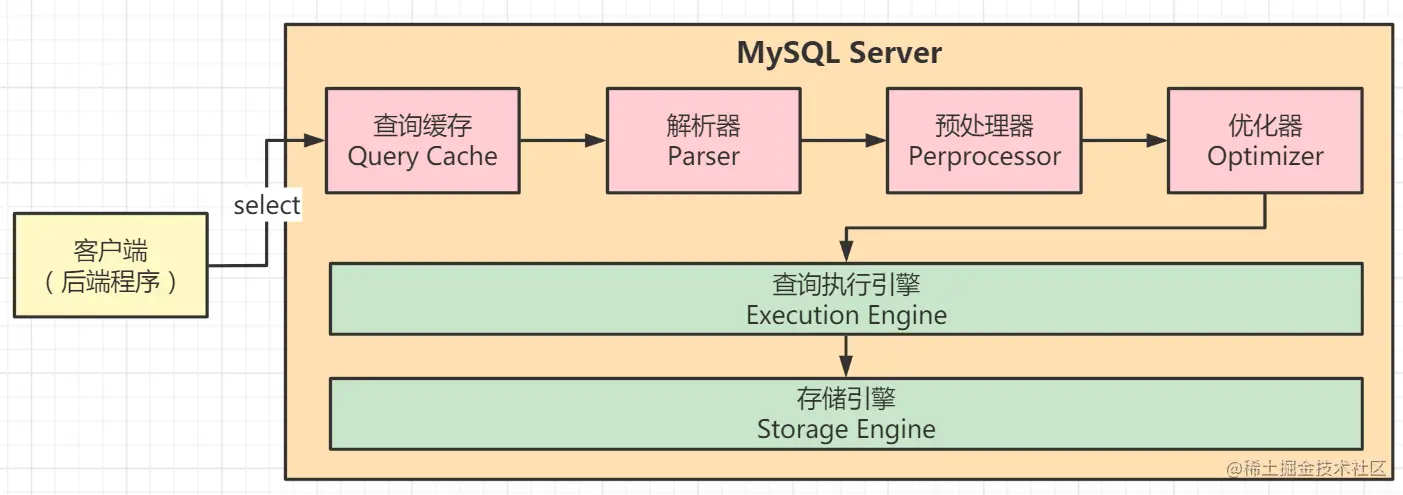
1.带锁的门在走廊上有n个带锁的门，从1到n依次编号。最初所有的门都是关着的。我们从门前经过n次，每一次都从1号门开始。在第i次经过时(i=1,2,…,n)我们改变i的整数倍号锁的状态:如果门是关的，就打开它;如果门是打开的，就关上它。在最后一次经过后，哪些门是打开的，哪些门是关上的?有多少打开的门?

package Demo1;

import java.util.Scanner;

public class ss2 {
    public static void main (String[] args){
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        int number=0;
        int close[] =new int[n+1];
        for (int i=0;i<n;i++){
            int j=i+1;
            if(j*j<=n){
                close[(int) Math.pow(j,2)]++;
            }
        }
        System.out.println("打开的编号：");
        for (int i=1;i<=n;i++){
            if(close[i]==1){
                System.out.println(i+"");
                number++;
            }
        }
        System.out.println("\n关门的编号");
        for(int i=1;i<=n;i++){
            if(close[i] !=1){
                System.out.println(i+"");
            }
        }
        System.out.println("\n开门数："+number);
    }
}

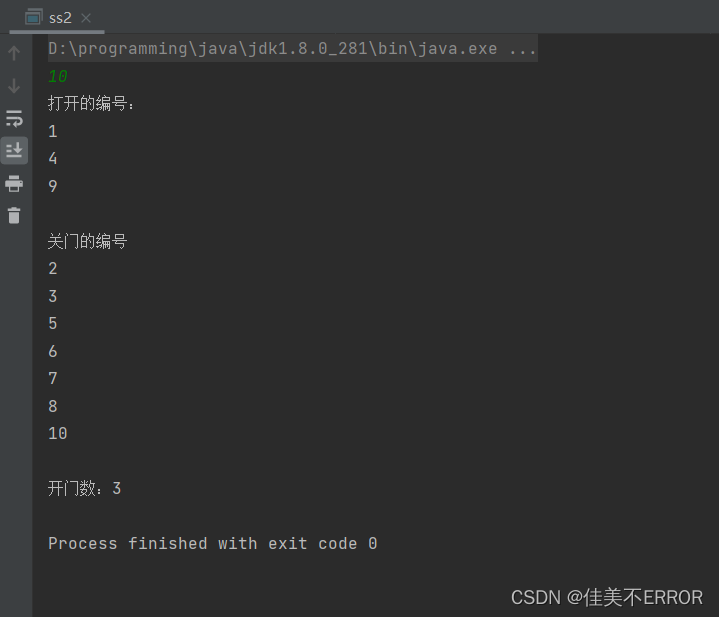
在这里插入图片描述

2.现代谜题有4个人打算过桥，他们都在桥的某一端。我们有17分钟让他们全部到达大桥的另一头。时间是晚上，他们只有一只手电筒。一次最多只能有两个人同时过桥，而且必须携带手电筒。必须步行将手电筒带来带去，即扔来扔去是不行的。每个人走路的速度不同:甲过桥要用1分钟，乙要用2分钟，丙要用5分钟，丁要用10分钟。两个人一起走的速度等于其中走得慢的那个人的速度。(注意，根据网上传言，西雅图附近一家著名软件公司的主考官就是用这个问题来考面试者的。)

甲乙先过去，甲回来，3分钟
丙丁过去，乙回来，12分钟
甲乙过去，2分钟
共计17分钟

package Demo1;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

public class ss3 {

        private static final String COMMA = ",";
        // 过桥规定时间不得多于17分钟
        private static final int SCHEDULT_TIME = 17;
        private static final String LEFT_SYMBOL = "{";
        private static final String RIGHT_SYMBOL = "}";
        private static final String GO_WORD = "过桥去了";
        private static final String BACK_WORD = "我又返回了";
        private static final String LEFT_ALLOW = "--->";
        private static final String RIGHT_ALLOW = "<---";
        private static final String NEW_LINE = "\n";

        private static int count = 1;

        private static Map<String, Integer> map = new HashMap<>();

        static {
            map.put("A", 1);
            map.put("B", 2);
            map.put("C", 5);
            map.put("D", 10);
        }

        public static void main(String[] args) {
            // TODO Auto-generated method stub
            List<String> list = new ArrayList<>();
            list.add("A");
            list.add("B");
            list.add("C");
            list.add("D");
            StringBuffer sb = new StringBuffer();
            int initTime = 0;
            new CrossBridge().resultCross(list, new ArrayList<String>(), initTime, sb);
        }

        /**
         * 处理过桥事件
         *
         * @param listNot
         *            未过桥人员列表
         * @param ListOver
         *            已过桥人员列表
         * @param initTime
         *            花费的时间
         * @param sb
         *            记录步骤过程
         */
        private void resultCross(List<String> listNot, List<String> ListOver, int initTime, StringBuffer sb) {

            // 获取未过桥的所有两两组合的可能组合
            List<String> result = getAllResult(listNot);

            for (String groupPeople : result) {
                // 因为列表数据是【a,b a,c a,d】这种格式
                String[] peoples = groupPeople.split(COMMA);
                //表示未过桥的人员列表
                List<String> current = new ArrayList<>(listNot);
                //表示已过桥的人员列表
                List<String> over = new ArrayList<>(ListOver);
                int currentTime = initTime;
                StringBuffer currentBuffer = sb;
                // 过桥后人数变动
                for (String people : peoples) {
                    // 未过桥列表减去过桥人员
                    current.remove(people);
                    // 已过桥列表增加过桥人员
                    over.add(people);
                }

                currentTime += getMaxTime(peoples);
                // 记录一条步骤--》{a,b}--->过桥去了
                currentBuffer.append(current).append(LEFT_ALLOW).append(LEFT_SYMBOL).append(groupPeople).append(RIGHT_SYMBOL).append(GO_WORD).append(LEFT_ALLOW).append(over).append(NEW_LINE);
                // 人员全部过完情况
                if (current.isEmpty()) {

                    if (currentTime <= SCHEDULT_TIME) {
                        System.out.println("第" + count + "种情况:");
                        System.out.println("花费时间--》" + currentTime);
                        System.out.println("步骤详情--》");
                        System.out.println(currentBuffer.toString());
                        count++;
                    }
                } else {
                    // 没有全部过桥情况，得从过桥列表中返回一个人
                    for (String peopleToBack : over) {
                        //表示已过桥的人员列表
                        List<String> overGroup = new ArrayList<>(over);
                        //表示未过桥的人员列表
                        List<String> waitGroup = new ArrayList<>(current);
                        int nowTime = currentTime;
                        StringBuffer nowBuffer = new StringBuffer(currentBuffer.toString());
                        // 已过桥列表删除返回的人员
                        overGroup.remove(peopleToBack);
                        // 未过桥列表增加返回的人员
                        waitGroup.add(peopleToBack);
                        // 加上返回时间
                        nowTime += map.get(peopleToBack);

                        // 返回的步骤
                        nowBuffer.append(waitGroup).append(RIGHT_ALLOW).append(LEFT_SYMBOL).append(peopleToBack).append(RIGHT_SYMBOL).append(BACK_WORD)
                                .append(RIGHT_ALLOW).append(overGroup).append(NEW_LINE);
                        // 递归，重新重复以上步骤
                        resultCross(waitGroup, overGroup, nowTime, nowBuffer);
                    }

                }

            }

        }

        /**
         * 返回时间最多的那个
         * @param peoples
         * @return
         */
        private int getMaxTime(String[] peoples) {
            // peoples[a，b],根据key找到存在map里面对应的时间，比较2者大小，返回最大时间
            return Math.max(map.get(peoples[0]), map.get(peoples[1]));
        }

        /**
         * 获取未过桥的所有两两组合的可能组合
         *
         * @param listNot
         *            未过桥人员列表
         * @return
         */
        private List<String> getAllResult(List<String> listNot) {
            // 把列表类型转换成字符串数组
            int len = listNot.size();
            String[] str = new String[len];
            listNot.toArray(str);
            int i, j;
            List<String> result = new ArrayList<>();
            for (i = 0; i < len - 1; i++) {
                for (j = 0; j < len; j++) {
                    // 如果组合是【a,a】或者result已经存在组合【a,b】还是【b,a】的情况就不往列表里加数据,其他组合加进列表。
                    if (!str[i].equals(str[j]) && !result.contains(str[i] + COMMA + str[j])
                            && !result.contains(str[j] + COMMA + str[i])) {
                        result.add(str[i] + COMMA + str[j]);
                    }
                }
            }
            // 组合格式：[A,B , A,C , A,D , B,C , B,D , C,D]
            return result;
        }

    }

3.页面编号 假设页面从1开始连续编号，共有1000页。计算所有页码中十进制数字的总个数。
分成四个区间
1-9，10-99，100-999，1000

4.名人问题n个人中的名人是指这样一个人:他不认识别人，但是每个人都认识他。任务就是找出这样一个名人，但只能通过询问“你认识他/她吗?”这种问是来完成。设计一个高效算法，找出该名人或者确定这群人中没有名人。你的算法在最坏情况下需要问多少个问题?

我们把人编号，比如从1 到 N。
我们考虑最坏情况：你问每一个人是否认识 X ，如果大家都认识，那么 X 一定是名人，如果其中一个人说不认识，那么那个人一定不是名人。因为 X 的范围是 1 到 N，所以，在最坏情况下，我们要问（N - 1） N 个问题。
但是，有一种更好的方法。我们从1开始，依次问他是否认识他的下一个，比如 2，如果 1 说认识，那么 1 一定不是名人，2 有可能是名人；如果1 说不认识，2 一定不是名人，1 却有可能是名人。这是这个方法巧的地方。所以，不管1 回答是还是不是，我们都可以确定其中一个不是名人，然后，我们继续问可能是名人那一位是否认识 3，然后依次下去，直到第 N 个人。这样我们就可以只要问（N - 1）个问题就可以把名人找出来。*

package Demo1;

import java.util.Stack;

public class ss4 {
     // Celebrity ID 2
        static int MATRIX[][] = {
                { 0, 0, 1, 0 },
                { 0, 0, 1, 0 },
                { 0, 0, 0, 0 },
                { 0, 0, 1, 0 }
        };

        // 如果a认识b,则返回true；否则返回 false
        static boolean knows(int a, int b) {
            boolean res = (MATRIX[a][b] == 1) ? true : false;
            return res;
        }


        // 如果名人celebrity存在，则返回 ID值，值的范围在 0到n-1之间；否则返回 -1
        static int findCelebrity(int n) {
            Stack<Integer> st = new Stack<>();
            int c;

            // Step 1 :把每一个人压入堆栈中
            for (int i = 0; i < n; i++) {
                st.push(i);
            }

            while (st.size() > 1) {
                // Step 2 :将前两个人弹出堆栈，根据已知（A，B）的返回状态丢弃一个人。
                int a = st.pop();
                int b = st.pop();

                // Step 3 : 将剩余的人压入堆栈中
                if (knows(a, b)) {
                    st.push(b);
                }

                else
                    st.push(a);
            }

            c = st.pop();

            // Step 4: 检查最后一个人是否是名人（Celebrity）
            for (int i = 0; i < n; i++) {

                //如果任何人都不是Celebrity；或者认识c或者a；或者认识任何人，则返回-1
                if (i != c && (knows(c, i) || !knows(i, c)))
                    return -1;
            }
            return c;
        }

        public static void main(String[] args) {
            int n = 4;
            int result = findCelebrity(n);
            if (result == -1) {
                System.out.println("No Celebrity");
            } else
                System.out.println("Celebrity ID " + result);
        }
    }

5.爬梯子 假设每一步可以爬一格或者两格梯子，爬一部n格梯子一共可以用几种方法?(例如，一部三格的梯子可以用三种不同的方法爬:1-1-1，1-2 和2-1。
要到达n阶台阶，必须从n-2阶跨两步，或者n-1阶跨一步
所以，n阶的方法f(n)可以为f(n-2)+f(n-1)

暴力方法（此方法会造成内存溢出）

   function climbStairs($n) {
    	if ($n<3) return $n;
        return climbStairs($n-2)+climbStairs($n-1);
    }

斐波那契函数（其实就是个f(n)=f(n-1)+f(n-2)）

 function climbStairs($n) {
    	$arr[1] = 1;
    	$arr[2] = 2;
    	for ($i=3;$i<=$n;$i++) {
    		$arr[$i] = $arr[$i-1]+$arr[$i-2];	
    	}
    	return $arr[$n];
    }

#递推 (动态规划思想)

f = [0] * 50
f[0] = 1
f[1] = 1
f[2] = 2
f[3] = 4
for i in range(4,50,1):
    f[i] = f[i-1] + f[i-2] + f[i-3]

print(f[4])
print(f[5])

6.交替放置的玻璃环有2n个玻璃杯挨个排成一行，前n个装满苏打水，其余n个杯子为空。交换杯子的位置，使之按照满一空一满一空的模式排列，而且杯子动的次数要最少([Gar78]，p.7)。
给2n个杯子从左至右从1开始依次编号，将第2个杯子与第n-1个杯子互换，那么此问题转化为2(n-2)个杯子的问题。交换次数M(n)=M(n-2)+1,当n>2时; M(1)=0;M(2)=1.

public class CupInsert {
static int count = 0;
public static void main(String[] args) {
System.out.println("请输入n的值(n>0):");
Scanner scanner = new Scanner(System.in);
String read = scanner.nextLine();
int n = Integer.parseInt(read);
arrayBulid(n);
System.out.println("杯子交换前的顺序(1-黑，0-白):");
for(int i=0;i<arrayBulid(n).length;i++){
System.out.print(arrayBulid(n)[i]+"--");
if((i+1)%10==0){
System.out.println(" ");
}
}
System.out.println(" ");
int[] result = cpuInsert(arrayBulid(n),n);
System.out.println("杯子交换后的顺序(1-黑，0-白):");
for(int i=0;i<=2*n-1;i++){
System.out.print(result[i]+"--");
if((i+1)%10==0){
System.out.println(" ");
}
}
System.out.println(" ");
System.out.println("交换的次数:"+count);
}
/*
*判断n为奇数还是偶数，然后交换杯子，得到交换杯子的序列以及交换次数
*/

private static int[] cpuInsert(int[] arrayBulid, int n) {
if(n%2==0){
for(int j=n;j<=2*n-1;j=j+2){
for(int i=0;i<n-1;i++){
if((arrayBulid[i]+arrayBulid[j]==1)&&(arrayBulid[i+1]+arrayBulid[j]==1)){
int t = arrayBulid[i+1];
arrayBulid[i+1]=arrayBulid[j];
arrayBulid[j]=t;
i=n-1;
}
}
count=count+1;
}
}else{
for(int j=n+1;j<=2*n-1;j=j+2){
for(int i=0;i<n-1;i++){
if((arrayBulid[i]+arrayBulid[j]==1)&&(arrayBulid[i+1]+arrayBulid[j]==1)){
int t = arrayBulid[i+1];
arrayBulid[i+1]=arrayBulid[j];
arrayBulid[j]=t;
}
}
count=count+1;
}
}

return arrayBulid;

}

/*
*构建存放原始杯子顺序的数组
*/
private static int[] arrayBulid(int n) {
int cup[] = new int[2*n];
for(int i=0;i<n;i++){
cup[i] = 1;
}
for(int i=n;i<2*n;i++){
cup[i] = 0;
}
return cup;
}

}

7.展会彩灯 早些年，在展会上可能会看到这样一种彩灯:一个被连接到若干开关上的电灯泡，只当所有开关都闭团合的时候才会发光。每一个开关由一个按钮控制;按下按钮就会切换开关状态，但是开关的状态是无法知道的。目标就是点亮灯泡。设计一个点亮灯泡的算法，使其在有n个开关时，在最坏的情况下，需要按动按钮的次数最少。

可以利用二进制反射格雷码的特性，相邻两个位串只相差一位数字，而2n个位串都是不同的。将n个开关分别对应n位二进制格雷码的每一位，每当格雷码的序列某一位发生变化，切换对应的开关状态。