数据结构实验 C语言 一元二项式操作

news2025/1/17 3:46:28
  • 东莞理工学院请勿抄袭

1.实验目的

通过实验达到：

⑴ 理解和掌握线性结构的概念及其典型操作的算法思想；

⑵ 熟练掌握基本线性结构-线性表的顺序存储结构、链式存储结构及其操作的实现；

⑶ 理解和掌握受限线性结构——堆栈、队列、串、数组的概念及其典型操作的算法思想、实现。

2. 实验题目1-一元多项式的操作

实验题目：一元多项式的操作。

实验要求：设有两个一元多项式：

p(x)=p0+p1x+p2x2+•••+pnxn

q(x)=q0+q1x+q2x2+•••+qmxm

:多项式项的系数为实数，指数为整数，设计实现一元多项式操作的程序：

① 多项式链表建立：以（系数，指数）方式输入项建立多项式，返回所建立的链表的头结点；

② 多项式排序：将所建立的多项式按指数非递减（从小到大）进行排序；

③ 多项式相加：实现两个多项式相加操作。操作生成一个新的多项式，原有的两个多项式不变，返回生成的多项式的头指针；

④多项式的输出：按照p0+p1x+p2x2+•••+pnxn格式输出多项式；

⑤主函数通过调用多项式链表建立函数，输入两个多项式并分别输出；输出排序后的两个多项式；分别调用多项式相加函数实现多项式相加、相减操作，分别输出操作结果。

测试数据：两个多项式均不少于4项，并且需要有同类项，至少一个同类项系数相反。

2.1. 数据结构设计

定义的数据结构如下：

  • 多项式节点结构体：
    • 系数可以为小数
    • 幂限制为整数
typedef struct Node {
	double coefficient;
	int power;
	struct Node* next;
}Node;
  • 多项式链式存储结构体：
typedef struct {
	int size;
	Node* head;
}Multinomial;

2.2. 主要操作算法设计与分析

2.2.1. 多项式创建函数算法设计

void menu() {
	printf("---------------------------------\n");
	printf("本次插入遇到同类项，您要如何处理？\n");
	printf("1. 忽略本次输入\n");
	printf("2. 覆盖原项\n");
	printf("3. 系数相加\n");
	printf("---------------------------------\n");
}

void choice(Node* cur, double d) {
    //选择后续操作函数

}

void create(Multinomial* pm, double d, int power) {
    //多项式添加节点创建函数
}


void menu1() {
	printf("------------------\n");
	printf("0. 退出\n");
	printf("1. 输入多项式\n");
	printf("2. 输出多项式\n");
	printf("3. 排序多项式\n");
	printf("------------------\n");
}

void createMultinomial(Multinomial* list) {
	//一条多项式的创建函数
}

void createMultinomial(Multinomial* list);

返回类型：无返回值；

是否有参数：有， 传入二项式链表，对此二项式链表变量修改

步骤：

  1. 进入循环调用menu1函数, 选择对应操作
  2. 选择1添加一个节点
  3. 调用create方法，并在控制台输入系数和幂，成功添加一个二项式节点
  4. 若出现此幂数对应的二项式节点存在，调用chice函数
    • 调用menu函数，选择忽略，覆盖，相加的其中一种操作
  5. 进行此操作直到选择0后退出，完成构造

算法时间复杂度：

  • 由于二项式链表，没有一个成员代表链表的末尾，每次都应该遍历链表到末尾
  • 所以时间复杂度为O(N);

2.2.2 二项式链表排序函数

Node* Sort(Node* head) {
    //二项式链表归并排序函数
}

void SortList(Multinomial* pm) {
	//二项式链表排序函数
}

void SortList(Multinomial* pm);

返回类型：无返回值；

是否有参数：有， 传入二项式链表，对此二项式链表变量修改

步骤：

  • 节点的大小取决于幂的大小
  1. 调用Sort函数，Sort函数的返回值赋值给pm指向的head
  2. 进入Sort函数后，进行归并排序
  3. 利用快慢指针平分链表，并打断链表
  4. 将左右链表传入Sort函数，即进入递归
  5. 当传入Sort的链表为空链表或者一个节点的链表时，返回此链表
  6. 在递归中接受两个Sort函数返回值，并进行合并有序链表操作
  7. 返回合并链表后的大链表

算法时间复杂度：

  • 归并排序时间复杂度：O(N * log2N)

2.2.3. 多项式输出函数

void display(Multinomial* pm) {
	//多项式输出函数
}

void display(Multinomial* pm);

返回类型：无返回值；

是否有参数：有， 传入二项式链表

步骤：

  1. 利用探路指针去遍历链表
  2. 对每一个节点进行分析并输出
  3. 系数为一或者负一应该省略1
  4. 幂为0应该省略x
  5. 幂小于0应该打括号
  6. 系数保留小数点后一位
  7. 系数小于0，二项式之间应该以减号分割，除非此二项式为首位
  8. 系数等于0，不显示
  9. 系数大于0， 位于首位不应该显示加号
  10. 最后打印回车

2.2.4. 多项式相加想减函数

void cre(Multinomial* pm, double d, int power) {
	//构造节点函数，为create函数的退化版本
}
void addition(Multinomial* pm1, Multinomial* pm2) {
	//多项式相加
}
void subtract(Multinomial* pm1, Multinomial* pm2) { // 【pm1 - pm2】左减右
	//多项式相减
}

void freeNode(Node* cur) {
	while (cur != NULL) {
		Node* tmp = cur;
		cur = cur->next;
		free(tmp);
	}
}

void addition(Multinomial* pm1, Multinomial* pm2);

void subtract(Multinomial* pm1, Multinomial* pm2);

返回类型：无返回值；

是否有参数：有， 传入两条二项式链表

对于多项式相加函数:

步骤：

  1. 将pm1与pm2两条链表的所有节点构造到一个新链表pm里
  2. 调用cre函数构造pm大链表
    • cre为create函数的退化，遇到同幂二项式，默认相加
  3. 排序pm二项式链表
  4. 输出pm二项式链表
  5. 调用freeNode函数释放pm链表

时间复杂度分析：O(N)

主要花费在构建pm链表上了

对于二项式链表相减函数，只需要在构建链表的时候，第二个二项式链表的节点的系数去相反数传入cre函数即可。

2.2.5. 主函数

void menu2() {
	printf("------------------------------------\n");
	printf("0. 退出\n");
	printf("1. 两个多项式相加\n");
	printf("2. 两个多项式相减（前面减后面）\n");
	printf("------------------------------------\n");

}

int main() {

	Multinomial list1 = { 0, NULL };
	Multinomial list2 = { 0, NULL };

	printf("输入第一个多项式\n");
	createMultinomial(&list1);
	printf("输入第二个多项式\n");
	createMultinomial(&list2);

	int input = 0;
	do {
		menu2();
		scanf("%d", &input);
		switch (input) {
		case 0:
			printf("退出成功\n");
			break;
		case 1:
			addition(&list1, &list2);
			break;
		case 2:
			subtract(&list1, &list2);
			break;
		default:
			printf("请重新输入\n");
			break;
		}
	} while (input);

	freeNode(list1.head);
	freeNode(list2.head);
	return 0;
}

步骤：

  1. 构造二项式链表1
    • 在构建的过程中可以输出显示二项式全貌
    • 在构造的过程中可以排序链表并输出排序后结果
  2. 构造二项式链表2
  3. 调用menu2菜单
  4. 选择相加或者相减操作
    • 相加/相减后输出结果
  5. 选择0退出
  6. 调用freeNode函数释放两条链表
  7. 程序结束

2.3. 程序运行过程及结果

  • 建立第一个二项式链表：

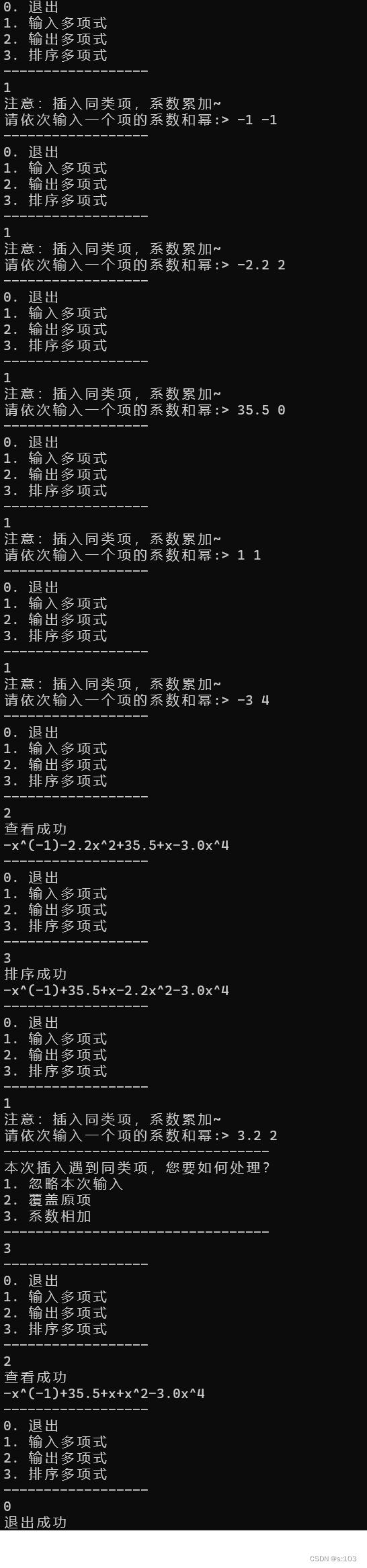
在这里插入图片描述

  • 建立第二个二项式链表：

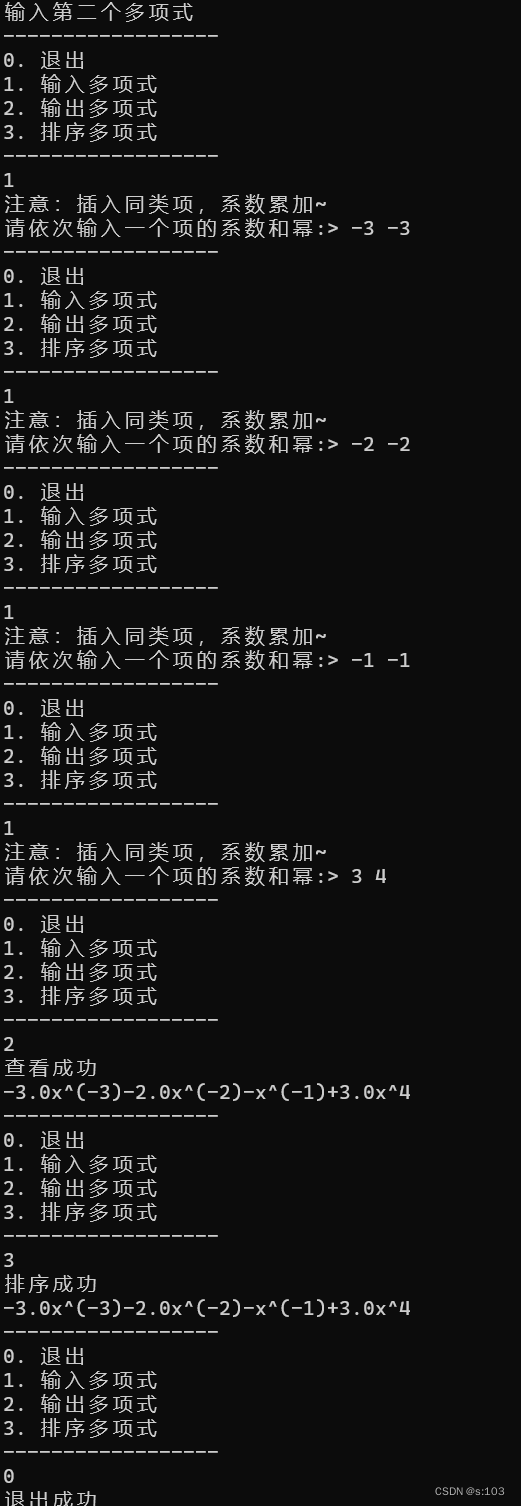
在这里插入图片描述

  • 相加相减二项式：

在这里插入图片描述

3. 总结

  • 在这个过程中遇到很多问题，例如空指针异常，结果与预计结果不符
  • 但是只要好好调试，总是能解决问题
  • 为了更加具有观赏性，优化输出
  • 对于一些代码仍存在改进空间，可以再简洁！
    • 例如利用函数指针数组减少switch的使用

4. 附录：源代码

4.1. 题目1 源代码：

4.1.1. basis.h头文件

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<math.h>

#define INIT 10

typedef struct Node {
	double coefficient;
	int power;
	struct Node* next;
}Node;

typedef struct {
	int size;
	Node* head;
}Multinomial;

Node* Sort(Node* head);
void SortList(Multinomial* pm);

void display(Multinomial* pm);
void addition(Multinomial* pm1, Multinomial* pm2);
void subtract(Multinomial* pm1, Multinomial* pm2);

void createReplace(Multinomial* pm, double d, int power);
void createGiveUp(Multinomial* pm, double d, int power);
void cre(Multinomial* pm, double d, int power);
void create(Multinomial* pm, double d, int power);
void freeNode(Node* cur);

4.1.2. Create.c 源文件

#include "basis.h"

void menu() {
	printf("---------------------------------\n");
	printf("本次插入遇到同类项，您要如何处理？\n");
	printf("1. 忽略本次输入\n");
	printf("2. 覆盖原项\n");
	printf("3. 系数相加\n");
	printf("---------------------------------\n");
}


void choice(Node* cur, double d) {
	int input = 0;
	menu();
	scanf("%d", &input);
	switch (input) {
	case 1:
		break;
	case 2:
		cur->coefficient = d;
		break;
	case 3:
		cur->coefficient += d;
		break;
	default:
		printf("插入失败\n");
		break;
	}

}

void create(Multinomial* pm, double d, int power) {
	Node* newOne = (Node*)malloc(sizeof(Node));
	newOne->next = NULL;
	newOne->power = power;
	newOne->coefficient = d;
	Node* cur = pm->head;
	pm->size++;
	if (cur == NULL) {
		pm->head = newOne;
		return;
	}
	while (cur->next != NULL) {
		if (cur->power == power) {
			pm->size--;//要减掉
			choice(cur, d);
			return;
		}
		cur = cur->next;
	}
	if (cur->power == power) {
		pm->size--;//要减掉
		choice(cur, d);
		return;
	}
	else {
		cur->next = newOne;
	}
}

void cre(Multinomial* pm, double d, int power) {
	Node* newOne = (Node*)malloc(sizeof(Node));
	newOne->next = NULL;
	newOne->power = power;
	newOne->coefficient = d;
	Node* cur = pm->head;
	pm->size++;
	if (cur == NULL) {
		pm->head = newOne;
		return;
	}
	while (cur->next != NULL) {
		if (cur->power == power) {
			pm->size--;//要减掉
			cur->coefficient += d;
			return;
		}
		cur = cur->next;
	}
	if (cur->power == power) {
		pm->size--;//要减掉
		cur->coefficient += d;
		return;
	}
	else {
		cur->next = newOne;
	}
}

4.1.3. Print.c源文件

#include"basis.h"
void display(Multinomial* pm) {
	Node* cur = pm->head;
	while (cur != NULL) {
		int power = cur->power;
		double d = cur->coefficient;
		if (d == 0) {
			cur = cur->next;
			continue;
		}
		if (d == 1) {
			if (power == 0) {
				printf("1");
			}
			else {
				if (cur != pm->head) {
					printf("+");
				}
				goto again;
			}
		}
		if (d == -1) {
			if (pow == 0) {
				printf("-1");
			}
			else {
				printf("-");
				goto again;
			}
		}
		if (cur == pm->head) {
			printf("%.1lf", cur->coefficient);
		}
		else {
			if (d > 0) {
				printf("+%.1lf", cur->coefficient);
			}
			else if (d < 0) {
				printf("%.1lf", cur->coefficient);
			}
			else {
				cur = cur->next;
				continue;
			}
		}
	again:
		if (power != 0) {
			if (power != 1) {
				if (power < 0) {
					printf("x^(%d)", power);
				}
				else {
					printf("x^%d", power);
				}
			}
			else {
				printf("x");
			}
		}
		cur = cur->next;
	}
	printf("\n");
}



void addition(Multinomial* pm1, Multinomial* pm2) {
	Multinomial newOne = { 0, NULL };
	Node* cur1 = pm1->head;
	Node* cur2 = pm2->head;
	while (cur1 != NULL) {
		cre(&newOne, cur1->coefficient, cur1->power);
		cur1 = cur1->next;
	}
	while (cur2 != NULL) {
		cre(&newOne, cur2->coefficient, cur2->power);
		cur2 = cur2->next;
	}
	SortList(&newOne);
	printf("两式想加为：\n");
	display(&newOne);
	freeNode(newOne.head);
}
void subtract(Multinomial* pm1, Multinomial* pm2) { // 【pm1 - pm2】
	Multinomial newOne = { 0, NULL };
	Node* cur1 = pm1->head;
	Node* cur2 = pm2->head;
	while (cur1 != NULL) {
		cre(&newOne, cur1->coefficient, cur1->power);
		cur1 = cur1->next;
	}
	while (cur2 != NULL) {
		cre(&newOne, -1 * cur2->coefficient, cur2->power);
		cur2 = cur2->next;
	}
	SortList(&newOne);
	printf("两式想减为：\n");
	display(&newOne);
	freeNode(newOne.head);
}

4.1.4. Sort.c 源文件

#include "basis.h"

Node* Sort(Node* head) {
	if (head == NULL || head->next == NULL) {
		return head;
	}
	Node* slow = head;
	Node* fast = head->next;
	//找到中间位置~
	while (fast != NULL && fast->next != NULL) {
		slow = slow->next;
		fast = fast->next->next;
	}
	Node* tmp = slow->next;
	slow->next = NULL;
	Node* left = Sort(head);
	Node* right = Sort(tmp);

	Node* ph = (Node*)malloc(sizeof(Node));
	Node* cur = ph;
	while (left != NULL && right != NULL) {
		if (left->power < right->power) {
			cur->next = left;
			left = left->next;
		}
		else {
			cur->next = right;
			right = right->next;
		}
		cur = cur->next;
	}
	cur->next = left != NULL ? left : right;
	tmp = ph->next;
	free(ph);
	return tmp;
}

void SortList(Multinomial* pm) {
	pm->head = Sort(pm->head);
}

4.1.5. Test.c源文件（main函数所在）

#include "basis.h"




void menu1() {
	printf("------------------\n");
	printf("0. 退出\n");
	printf("1. 输入多项式\n");
	printf("2. 输出多项式\n");
	printf("3. 排序多项式\n");
	printf("------------------\n");
}
void menu2() {
	printf("------------------------------------\n");
	printf("0. 退出\n");
	printf("1. 两个多项式相加\n");
	printf("2. 两个多项式相减（前面减后面）\n");
	printf("------------------------------------\n");

}

void createMultinomial(Multinomial* list) {
	int input = 0;
	do {
		menu1();
		scanf("%d", &input);
		switch (input) {
		case 0:
			printf("退出成功\n");
			break;
		case 1:
			printf("注意：插入同类项，系数累加~\n");
			printf("请依次输入一个项的系数和幂:> ");
			int power = 0;
			double d = 0;
			scanf("%lf%d", &d, &power);
			create(list, d, power);
			break;
		case 2:
			printf("查看成功\n");
			display(list);
			break;
		case 3:
			printf("排序成功\n");
			SortList(list);
			display(list);
			break;
		default:
			printf("请重新输入\n");
		}

	} while (input);
}


int main() {

	Multinomial list1 = { 0, NULL };
	Multinomial list2 = { 0, NULL };

	printf("输入第一个多项式\n");
	createMultinomial(&list1);
	printf("输入第二个多项式\n");
	createMultinomial(&list2);

	int input = 0;
	do {
		menu2();
		scanf("%d", &input);
		switch (input) {
		case 0:
			printf("退出成功\n");
			break;
		case 1:
			addition(&list1, &list2);
			break;
		case 2:
			subtract(&list1, &list2);
			break;
		default:
			printf("请重新输入\n");
			break;
		}
	} while (input);

	freeNode(list1.head);
	freeNode(list2.head);
	return 0;
}

//free链表函数
void freeNode(Node* cur) {
	while (cur != NULL) {
		Node* tmp = cur;
		cur = cur->next;
		free(tmp);
	}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/443526.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

HTTP 1 2 3 的演变过程

HTTP 1 2 3 的演变过程

1 HTTP/1.1 相比 HTTP/1.0 提高了什么性能&#xff1f; HTTP/1.1 相比 HTTP/1.0 性能上的改进&#xff1a; 使用长连接的方式改善了 HTTP/1.0 短连接造成的性能开销。支持管道&#xff08;pipeline&#xff09;网络传输&#xff0c;只要第一个请求发出去了&#xff0c;不必等…
阅读更多...
【ECharts+Vue】学习笔记（快速入门版）

【ECharts+Vue】学习笔记（快速入门版）

一、ECharts 1.1 什么是Echarts ECharts 是一个使用 JavaScript 实现的开源可视化库&#xff0c;涵盖各行业图表&#xff0c;满足各种需求。提供了丰富的可视化图标&#xff0c;帮助你轻松实现大屏展示。 官网地址&#xff1a;Apache ECharts 1.2 ECharts的安装 直接下载 下载官…
阅读更多...
分布式之搜索解决方案es

分布式之搜索解决方案es

一 ES初识 1.1 概述 ElasticSearch&#xff1a;是基于 Lucene 的 Restful 的分布式实时全文搜索引擎&#xff0c;每个字段都被索引并可被搜索&#xff0c;可以快速存储、搜索、分析海量的数据。是ELK的一个组成,是一个产品&#xff0c;而且是非常完善的产品&#xff0c;ELK代表…
阅读更多...
webRtc播放rtsp视频流（vue2、vue3+vite+ts）

webRtc播放rtsp视频流（vue2、vue3+vite+ts）

一、下载webRtc 开发环境用的win10版本的。 github上直接下载&#xff0c;速度感人。 Releases mpromonet/webrtc-streamer GitHub 提供资源下载&#xff0c;0积分 https://download.csdn.net/download/weiqiang915/87700892 二、启动&#xff0c;测试 webrtc-streame…
阅读更多...
PDD滑块分析

PDD滑块分析

文章目录 1.流程分析2.关键点分析3.结果展示 声明&#xff1a;本文只作学习研究&#xff0c;禁止用于非法用途&#xff0c;否则后果自负&#xff0c;如有侵权&#xff0c;请告知删除&#xff0c;谢谢&#xff01; 欢迎大佬加群一起交流哇&#xff08; Q群&#xff1a;985475126…
阅读更多...
基于web的电动车租赁管理系统C#+asp.net+sqlserver

基于web的电动车租赁管理系统C#+asp.net+sqlserver

具体功能如下&#xff1a;个人信息管理&#xff1a;实现登陆后对个人信息进行修改和查看的功能。 修改登录密码&#xff1a;实现登陆后对个人密码进行修改的功能。 申请租车订单&#xff1a;客户用户登陆后可以申请租车订单。同时可以查看租赁订单信息。 售后评价管理&#xff…
阅读更多...
深度学习中的一阶段目标检测

深度学习中的一阶段目标检测

博主简介 博主是一名大二学生&#xff0c;主攻人工智能研究。感谢让我们在CSDN相遇&#xff0c;博主致力于在这里分享关于人工智能&#xff0c;c&#xff0c;Python&#xff0c;爬虫等方面知识的分享。 如果有需要的小伙伴可以关注博主&#xff0c;博主会继续更新的&#xff0c…
阅读更多...
飞行机器人专栏（十二）-- 提高机器人系统可靠性的关键要素与实践

飞行机器人专栏（十二）-- 提高机器人系统可靠性的关键要素与实践

本文将介绍如何在机器人系统的开发过程中融入关键要素&#xff0c;从而提高系统的可靠性。我们将从需求分析、设计阶段、开发与调试、验证与优化、迭代与升级等方面进行详细讨论&#xff0c;并提供示例代码以帮助您更好地理解相关概念。 目录 一、需求分析与规划 二、…
阅读更多...
XML与JSON知识学习

XML与JSON知识学习

目录 XML简介 XML的结构 小结 使用DOM 练习 小结 使用SAX 练习 小结 使用Jackson 练习 小结 使用JSON 反序列化 练习 小结 XML简介 XML是可扩展标记语言&#xff08;eXtensible Markup Language&#xff09;的缩写&#xff0c;它是一种数据表示格式&#xf…
阅读更多...
管理后台项目-01-项目模板-登录相关-路由搭建-品牌相关

管理后台项目-01-项目模板-登录相关-路由搭建-品牌相关

目录 1-项目模板 1.1-项目目录结构说明​编辑 1.2-前置项目相关配置 2-登录相关开发 3-路由的搭建 4-品牌管理 4.1-品牌列表 4.2-新增/修改品牌 4.3-删除品牌名称 1-项目模板 前端的后台管理系统我们采用github上有的成熟项目作为模板来开发&#xff1b; 简洁版:GitHu…
阅读更多...
【CocosCreator入门】CocosCreator组件 | ScrollView（滚动视图）组件

【CocosCreator入门】CocosCreator组件 | ScrollView（滚动视图）组件

Cocos Creator 是一款流行的游戏开发引擎&#xff0c;具有丰富的组件和工具&#xff0c;其中的ScrollView组件是一种用于实现滚动视图效果的重要组件。它可以让我们在游戏中实现各种滚动视图效果&#xff0c;例如列表、地图等。 目录 一、组件介绍 二、组件属性 三、详细说明…
阅读更多...
java+mysql crm客户关系管理系统的设计与实现

java+mysql crm客户关系管理系统的设计与实现

在众多网站开发技术中，JSP支持现在绝大多数操作平台，它在代码执行效率、代码可移植性及组建的应用上均优越于其他动态网页技术。因此，本文研究了基于JSP技术的系统动态网站。根据JSP的原理按照网站时机原则以及步骤，对动态网站的定义了目标、分析了网站功能需求，进行了结构…
阅读更多...
windows 10 下安装配置mysql8.0 （保姆级教程）

windows 10 下安装配置mysql8.0 （保姆级教程）

文章目录 一、MySQL 8.0的基本信息二、MySQL 8.0的系统要求三、MySQL 8.0的安装步骤3.1. 下载MySQL 8.03.2. 运行MySQL安装文件3.3. 选择安装类型3.4. 配置MySQL Server3.5 mysql shell 的使用 四、总结 一、MySQL 8.0的基本信息 MySQL是一种开放源代码的关系型数据库管理系统…
阅读更多...
2023Java高频面试题，jvm虚拟机体系结构，收藏必看！

2023Java高频面试题，jvm虚拟机体系结构，收藏必看！

1. 前言 最近很多小伙伴在找工作. 在面试中, 面试官经常问到的一个面试题是 : 请说出Jvm虚拟机体系结构? 小伙伴们, 一般会说堆, 栈.....然后面试官问, 那还知道其他的吗, 然后小伙伴们就语塞了....... 面试后来问千锋健哥, 所以健哥在这里为大家来讲讲这个Jvm虚拟机体系结…
阅读更多...
【一起啃书】《机器学习》第三章 线性模型

【一起啃书】《机器学习》第三章 线性模型

第三章 线性模型 3.1 基本形式 给定由 d d d个属性描述的示例 x ( x 1 ; x 2 ; . . . ; x d ) {\bf{x}} ({x_1};{x_2};...;{x_d}) x(x1​;x2​;...;xd​)&#xff0c;其中 x i x_i xi​是 x \bf{x} x在第 i i i个属性上的取值&#xff0c;线性模型试图学得一个通过属性的线性…
阅读更多...
瀚高股份吕新杰：创新开源双驱动，躬耕国产数据库

瀚高股份吕新杰：创新开源双驱动，躬耕国产数据库

作者 | 伍杏玲 近年来&#xff0c;国际形势不断变幻&#xff0c;也给人们带来巨大警示&#xff1a;关键核心技术是买不来、讨不来的&#xff0c;中国科技企业需寻找研发自强之路。 瀚高基础软件股份有限公司&#xff08;简称瀚高股份&#xff09;专注数据库十八年&#xff0c;始…
阅读更多...
信息安全-reNgine-Web应用渗透测试的自动化网络侦察框架

信息安全-reNgine-Web应用渗透测试的自动化网络侦察框架

目录 reNgine介绍 工具运行机制 安装部署 安装rengine 安装python依赖包 合并Django前端静态文件 安装Postgresql 创建reNgine账号 启动reNgine 启动reNgine成功 启动reNgine后在浏览器访问&#xff1a;http://localhost:8000/ 这时会发现前端静态资源加载失败&…
阅读更多...
【自然语言处理】【大模型】极低资源微调大模型方法LoRA以及BLOOM-LORA实现代码

【自然语言处理】【大模型】极低资源微调大模型方法LoRA以及BLOOM-LORA实现代码

极低资源微调大模型方法LoRA以及BLOOM-LORA实现代码 相关博客 【自然语言处理】【大模型】极低资源微调大模型方法LoRA以及BLOOM-LORA实现代码 【自然语言处理】【大模型】DeepMind的大模型Gopher 【自然语言处理】【大模型】Chinchilla&#xff1a;训练计算利用率最优的大语言…
阅读更多...
Froala V4.0.18 Crack Froala 编辑器

Froala V4.0.18 Crack Froala 编辑器

Froala V4.0.18&#xff1a;复制和粘贴图像变得更好&#xff0c;还有更多&#xff01; 2023 年 3 月 25 日最忠实用户编辑器&#xff0c;新版本发表评论 Froala Editor团队很高兴地宣布发布Froala Editor 4.0.18。这个新版本在质量和稳定性方面有很多改进&#xff0c;并修复了…
阅读更多...
优雅的处理sping项目全局异常

优雅的处理sping项目全局异常

全局异常处理 为了达到系统的各个模块中都能够共用同一个异常处理逻辑&#xff0c;避免代码重复和错误。在Spring框架中&#xff0c;可以通过全局异常处理来捕获应用程序中抛出的异常&#xff0c;并根据需要进行处理。 ControllerAdvice ControllerAdvice是Spring MVC框架中…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023