目录
1.快速排序核心思路
2.挖坑法快速排序(递归)
2.1步骤
2.2代码(详细注释)
3.非递归快排(用栈实现快速排序)
3.1思路
3.2代码
4.二路快排
4.1思路
4.2代码
5.三路快排
5.1思路
5.2代码
1.快速排序核心思路
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
(1)首先设定一个分界值,通过该分界值将数组分成左右两部分。
(2)将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于分界值,而右边部分中各元素都大于或等于分界值。
(3)然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程。
补充:选取分区点时尽可能的随机,保证分区点两侧都有元素。
分区点的选择:
1.三数取中法:在无序数组的首,中,尾这三个数据中,选择一个排在中间的数据作为分区点。
2.随机数法:在无序数组中随机选取一个数作为分区点。
2.挖坑法快速排序(递归)
2.1步骤
1.设定一个分区点(一般为序列的最左边元素,也可以是最右变的元素)此时最左边的是一个坑。这里选择最左边元素7作为分区点。

2.开辟两个指针,分别指向序列的头结点和尾结点(选取的分区点在左边,则先从右边出发。反之,选取的分区点在右边,则先从左边出发)。
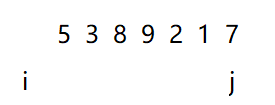
3.从右指针出发依次遍历序列,如果找到一个值比所选的分区点要小,则将此指针所指的值放在坑里,左指针向前移。此时j遍历到1这个位置,1<7,将1填入i所指的坑里。
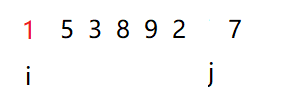
4.后从左指针出发(选取的分区点在左边,则后从左边出发。反之,选取的分区点在右边,则后从右边出发),依次便利序列,如果找到一个值比所选的分区点要大,则将此指针所指的值放在坑里,右指针向前移。
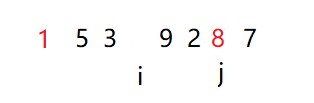
5. 依次循环步骤4,5,直到左指针和右指针重合时,我们把分区点放入这连个指针重合的位置。

2.2代码(详细注释)
//挖坑法快速排序
public static void quickSortHole(int[] arr){
quickSortInternal(arr,0,arr.length);
}
private static void quickSortInternal(int[] arr, int l, int r) {
//小数组使用直接插入排序最快
if(r-l<=64){
insertionSort(arr,l,r);
return;
}
//先找到第一次排序后分区点的索引
int p=partitionByHole(arr,l,r);
//将分区点左边元素进行快速排序
quickSortInternal(arr,l,p-1);
//将分区点右边元素进行快速排序
quickSortInternal(arr,p+1,r);
}
private static int partitionByHole(int[] arr, int l, int r) {
//这里分区点定位最左边的值
int pivot=arr[l];
//两个指针,分别指向序列的头节点和尾节点
int i=l;
int j=r;
while(i<j){
//先从后向前遍历
while(i<j && arr[j]>pivot){
j--;
}
//此时j指针停在第一个小于pivot的地方,将这个值放入i所指的坑里,那么j所指的地方就变为了一个坑
swap(arr,i,j);
//然后从前向后遍历
while(i<j && arr[i]<pivot){
i++;
}
//此时i指针停在第一个大于pivot的地方,将这个值放入j所指的坑里
swap(arr,i,j);
}
//此时,i和j指向同一位置,回填分区点
arr[i]=pivot;
return i;
}
//直接插入排序,选取无序区间的第一个元素插入到有序区间的正确位置上
private static void insertionSort(int[] arr, int l, int r) {
//无序区间[i,r)
//有序区间[l,i)
//无序区间的每一个元素遍历一遍
for(int i=l+1;i<r;i++){
//将无序区间的第一个元素与有序区间的元素比较
for(int j=i;j>l;j--){
if(arr[j]<arr[j-1]){
swap(arr,j,j-1);
}
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
3.非递归快排(用栈实现快速排序)
3.1思路
递归调用的本质就是栈,栈是一个先进后出的数据结构。
1.将区间的左右两边入栈。让right取栈顶元素(是我们后入的区间的右边),再删除栈顶的元素。同样,让left取先入但是后出的元素(区间的左边)。此时我们拿到了一个区间[left,right],我们对这个区间进行一次快速排序。
2.此时一个分区点到了正确的位置,我们继续对左边区间和右边区间的首尾入栈。
3.当栈为空时,说明排序完成。
3.2代码
//非递归的快排(栈)
public static void quickSortNonRecursion(int[] arr){
Deque<Integer>stack=new ArrayDeque<>();
stack.push(arr.length-1);
stack.push(0);
while(!stack.isEmpty()){
int l=stack.pop();
int r=stack.pop();
if(l>=r){
continue;
}
int p=partitionByHole(arr,l,r);
//处理左半区间
stack.push(p-1);
stack.push(l);
//处理右半区间
stack.push(r);
stack.push(p+1);
}
}
private static int partitionByHole(int[] arr, int l, int r) {
//这里分区点定位最左边的值
int pivot=arr[l];
//两个指针,分别指向序列的头节点和尾节点
int i=l;
int j=r;
while(i<j){
//先从后向前遍历
while(i<j && arr[j]>pivot){
j--;
}
//此时j指针停在第一个小于pivot的地方,将这个值放入i所指的坑里,那么j所指的地方就变为了一个坑
swap(arr,i,j);
//然后从前向后遍历
while(i<j && arr[i]<pivot){
i++;
}
//此时i指针停在第一个大于pivot的地方,将这个值放入j所指的坑里
swap(arr,i,j);
}
//此时,i和j指向同一位置,回填分区点
arr[i]=pivot;
return i;
}
//直接插入排序,选取无序区间的第一个元素插入到有序区间的正确位置上
private static void insertionSort(int[] arr, int l, int r) {
//无序区间[i,r)
//有序区间[l,i)
//无序区间的每一个元素遍历一遍
for(int i=l+1;i<r;i++){
//将无序区间的第一个元素与有序区间的元素比较
for(int j=i;j>l;j--){
if(arr[j]<arr[j-1]){
swap(arr,j,j-1);
}
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}4.二路快排
对于上面我写的快排,将小于等于基准值的数据全都放到了左边,大于的放到右边了,那么这样就会出现问题。不管是当条件大于等于还是小于等于,当数组中重复元素非常多的时候,等于基准值的元素太多,那么数组就会分成极度不平衡的两个部分,因为等于基准值的一部分总是集中在数组的一边。
此时,使用二路快排就可以进行优化,阻止效率的降低。
4.1思路
1.正如其名,选取最左边为分区点,将整个区间分为两条路,一路是大于等于分区点的元素(橙色部分),一路是小于与分区点的元素(粉色部分)。分区点v的下标此时为l,i指向当前正在扫描的数组元素。区间[l+1,j]为小于分区点的元素区间,区间[j+1,i]为大于等于分区点元素的区间。
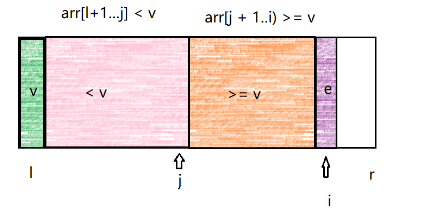
2.当arr[i]>=v时,直接i++即可。
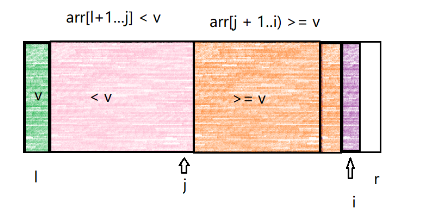
3.当arr[i]<v时,交换arr[j+1]和arr[i]。然后j++。
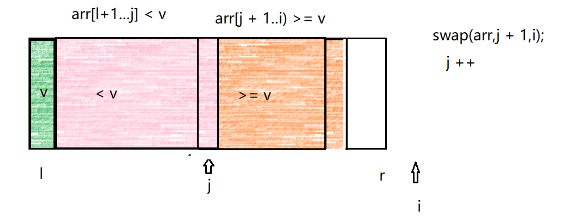
4.当扫描完数组之后,将分区点和j所指元素交换,回填分区点,数组为如下分区。
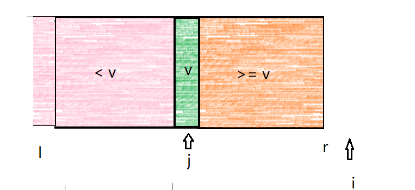
4.2代码
//二路快排
public static void quickSort2(int[] arr){
quickSortInternal(arr,0,arr.length);
}
private static void quickSortInternal(int[] arr, int l, int r) {
if(r-l<=64){
insertionSort(arr,l,r);
return;
}
int p=partition(arr,l,r);
quickSortInternal(arr,l,p-1);
quickSortInternal(arr,p+1,r);
}
private static int partition(int[] arr, int l, int r) {
//最左边元素作为分区点
int v=arr[l];
//初始j指向l
int j=l;
//初始i指向分区点后面第一个元素
for(int i=l+1;i<r;i++){
if(arr[i]<v){
swap(arr,i,j+1);
j++;
}
}
//回填分区点
swap(arr,l,j);
return j;
}5.三路快排
三路快排就是在快速排序的基础上进一步优化的,它将数据分为三个部分:大于分区点,小于分区点和等于分区点。
5.1思路
1.将数据分为三个部分,i指向当前数组正在处理的元素。
区间[l+1,lt]为小于分区点的元素区间
区间[lt+1,i]为等于分区点的元素区间
区间[gt,r]为大于分区点的元素区间
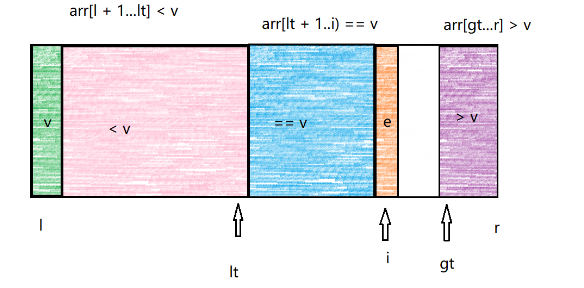
2.当arr[i]==v时,i++即可。
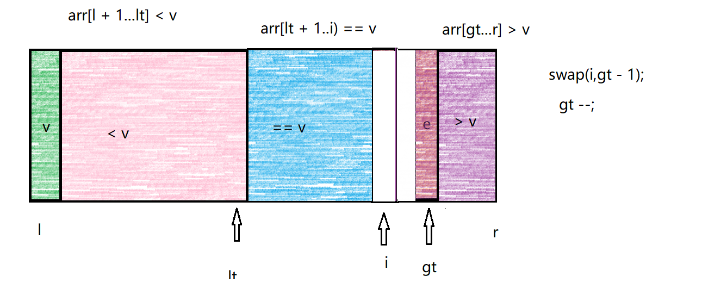
3.当arr[i]>v时,交换arr[i]和arr[gt-1]
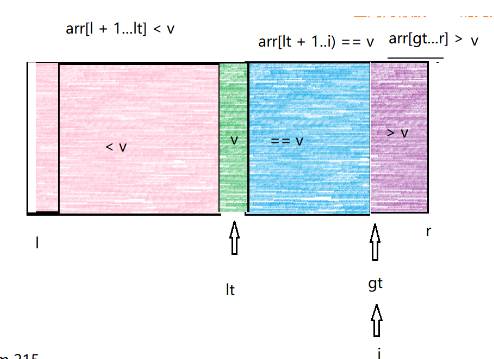
4.当arr[i]<v时,交换arr[i]和arr[lt]。当i和gt重合时,整个数组交换完毕。
5.2代码
//三路快排
public static void quickSort3(int[] arr){
quickSortInternal3(arr,0,arr.length-1);
}
private static void quickSortInternal3(int[] arr, int l, int r) {
if(r-l<=64){
insertionSort(arr,l,r);
return;
}
int v=arr[l];
int lt=l;
int gt=r+1;
int i=l+1;
//终止条件为i和gt重合
while(i<gt){
if(arr[i]<v){
swap(arr,lt+1,i);
lt++;
i++;
}else if(arr[i]>v){
swap(arr,gt-1,i);
gt--;
}else{
i++;
}
}
//回填分区点
swap(arr,l,lt);
quickSortInternal3(arr,l,lt-1);
quickSortInternal3(arr,gt,r);
}