数字信号预处理
对信号进行去噪、平滑和去趋势处理,为进一步分析做好准备。从数据中去除噪声、离群值和乱真内容。增强信号以对其可视化并发现模式。更改信号的采样率,或者使不规则采样信号或带缺失数据信号的采样率趋于恒定。为仿真和算法测试生成脉冲信号和 chirp 等合成信号。
平滑和去噪
Savitzky-Golay 平滑、中位数和 Hampel 滤波、去趋势
目的:从信号中去除不需要的峰值、趋势和离群值。
方法:使用 Savitzky-Golay 滤波器、移动平均值、移动中位数、线性回归或二次回归对信号进行平滑处理。
函数
| detrend | 去除多项式趋势 |
| filloutliers | 检测并替换数据中的离群值 |
| hampel | Outlier removal using Hampel identifier |
| isoutlier | 查找数据中的离群值 |
| medfilt1 | 1-D median filtering |
| movmad | 移动中位数绝对偏差 |
| movmedian | 移动中位数 |
| sgolay | Savitzky-Golay filter design |
| sgolayfilt | Savitzky-Golay filtering |
| smoothdata | 对含噪数据进行平滑处理 |
信号平滑处理
发现数据中的重要模式,同时排除噪声、离群值和其他不相关信息。
此示例说明如何使用移动平均滤波器和重采样来隔离一天中时间的周期性分量对每小时温度读数的影响,以及如何去除开环电压测量中不需要的电线噪声。该示例还说明如何通过使用中位数滤波器对时钟信号的水平进行平滑处理,同时保留边沿。该示例还说明如何使用 Hampel 滤波器去除大的离群值。
目的
通过平滑处理,我们可以发现数据中的重要模式,同时忽略不重要的内容(如噪声)。我们使用滤波来执行这种平滑处理。平滑处理的目标是呈现值的缓慢变化情况,以便更容易看到数据的趋势。
有时,当您检查输入数据时,您可能希望平滑处理数据以便看到信号的趋势。在我们的示例中,我们有一组 2011 年 1 月在波士顿洛根机场每小时的摄氏温度读数。
load bostemp
figure
days = (1:31*24)/24;
plot(days, tempC)
axis tight
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')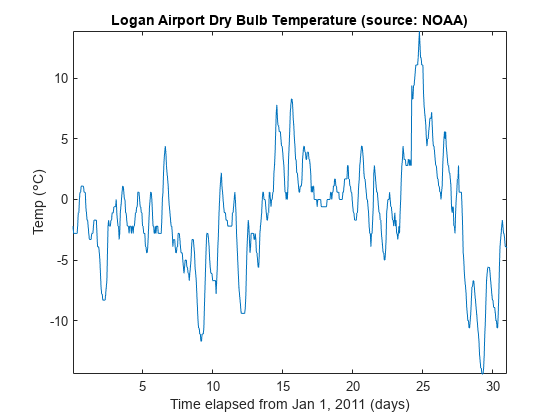
请注意,我们可以直观地看到一天中的时间对温度读数的影响。如果您只关注月内的每日温度变化,则每小时的波动只会产生噪声,使得每日的变化很难辨别。为了去除时间的影响,我们现在希望使用移动平均滤波器来平滑处理数据。
一种移动平均滤波器
移动平均滤波器的最简单形式是其长度为 N 并且取波形的每 N 个连续采样的平均值。
为了对每个数据点应用移动平均滤波器,我们构造滤波器的系数,使得每个点的权重相等且占比为总均值的 1/24。这样我们可以得出每 24 小时的平均温度。
hoursPerDay = 24;
coeff24hMA = ones(1, hoursPerDay)/hoursPerDay;
avg24hTempC = filter(coeff24hMA, 1, tempC);
% figure
plot(days,[tempC avg24hTempC])
legend('Hourly Temp','24 Hour Average (delayed)','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')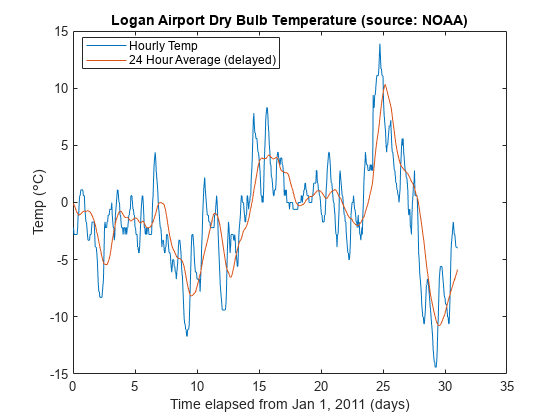
滤波器延迟
请注意,滤波后的输出存在大约 12 个小时的延迟。这是因为我们的移动平均滤波器有延迟。
长度为 N 的任何对称滤波器都存在 (N-1)/2 个采样的延迟。我们可以人为去除这种延迟。
figure
fDelay = (length(coeff24hMA)-1)/2;
plot(days,tempC,days-fDelay/24,avg24hTempC)
axis tight
legend('Hourly Temp','24 Hour Average','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')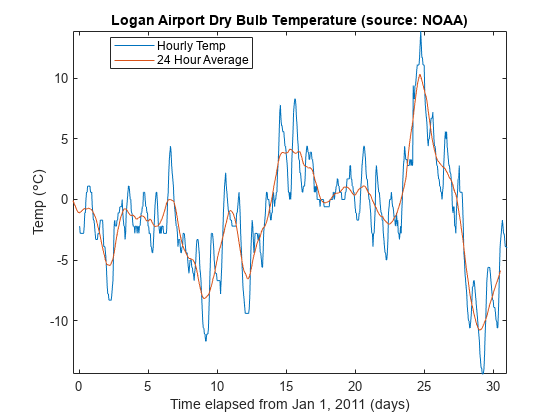
提取平均差异
我们也可以使用移动平均滤波器来更好地估计一天中的时间如何影响整体温度。为此,首先从每小时的温度测量值中减去平滑处理后的数据。然后,将差异数据按天数分割,取月中所有 31 天的平均值。
figure
deltaTempC = tempC - avg24hTempC;
deltaTempC = reshape(deltaTempC, 24, 31).';
plot(1:24, mean(deltaTempC))
axis tight
title('Mean temperature differential from 24 hour average')
xlabel('Hour of day (since midnight)')
ylabel('Temperature difference (\circC)')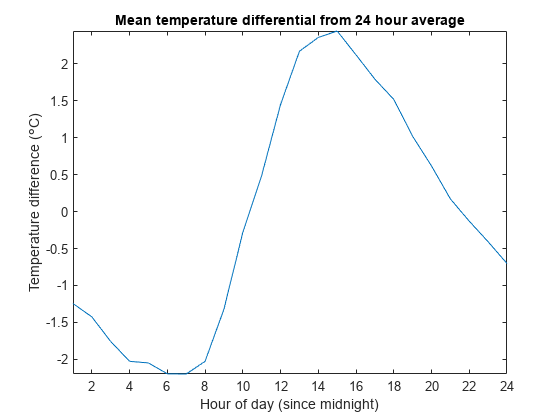
提取峰值包络
温度信号的高低每天都有变化,有时我们也希望对这种变化有平滑变动的估计。为此,我们可以使用 envelope 函数来连接在 24 小时内的某个时段检测到的极端高点和极端低点。在此示例中,我们确保在每个极端高点和极端低点之间有至少 16 个小时。我们还可以通过取两个极端点之间的平均值来了解高点和低点的趋势。
figure
[envHigh, envLow] = envelope(tempC,16,'peak');%envelope(x,np,'peak'):返回x的上、下峰包络。包络由至少np个样本分开的局部极大值上使用样条插值确定。
envMean = (envHigh+envLow)/2;
plot(days,tempC, ...
days,envHigh, ...
days,envMean, ...
days,envLow)
axis tight
legend('Hourly Temp','High','Mean','Low','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')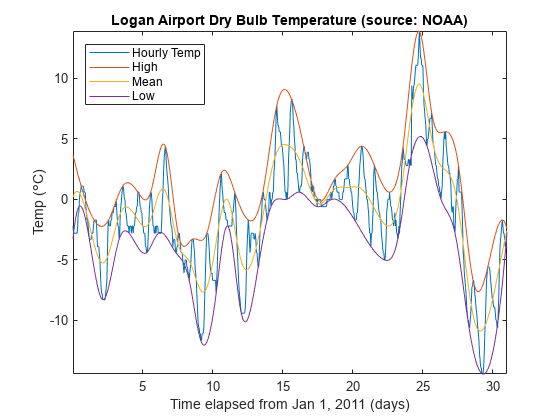
加权移动平均滤波器
其他类型的移动平均滤波器并不对每个采样进行同等加权。
另一种常见滤波器遵循 [1/2,1/2]^n 的二项式展开。对于大的 n 值,这种类型的滤波器逼近正态曲线。对于小的 n 值,这种滤波器适合滤除高频噪声。要找到二项式滤波器的系数,请对 [1/2,1/2] 进行自身卷积,然后用 [1/2,1/2] 与输出以迭代方式进行指定次数的卷积。在此示例中,总共使用五次迭代。
h = [1/2 1/2];
binomialCoeff = conv(h,h);
for n = 1:4
binomialCoeff = conv(binomialCoeff,h);
end
figure
fDelay = (length(binomialCoeff)-1)/2;
binomialMA = filter(binomialCoeff, 1, tempC);
plot(days,tempC, ...
days-fDelay/24,binomialMA)
axis tight
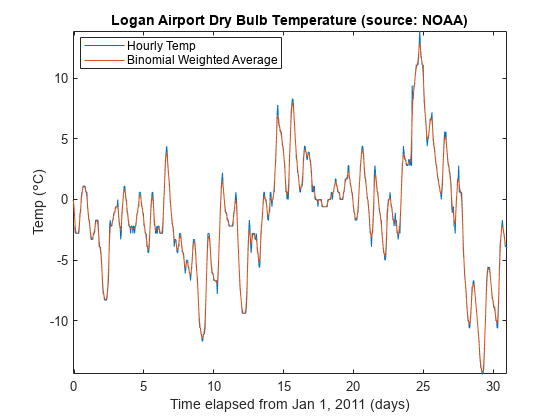
legend('Hourly Temp','Binomial Weighted Average','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')
指数移动平均滤波器
另一种有点类似高斯展开滤波器的滤波器是指数移动平均滤波器。这种类型的加权移动平均滤波器易于构造,并且不需要大的窗大小。
可以通过介于 0 和 1 之间的 alpha 参数来调整指数加权移动平均滤波器。alpha 值越高,平滑度越低。
alpha = 0.45;
exponentialMA = filter(alpha, [1 alpha-1], tempC);
plot(days,tempC, ...
days-fDelay/24,binomialMA, ...
days-1/24,exponentialMA)
axis tight
legend('Hourly Temp', ...
'Binomial Weighted Average', ...
'Exponential Weighted Average','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')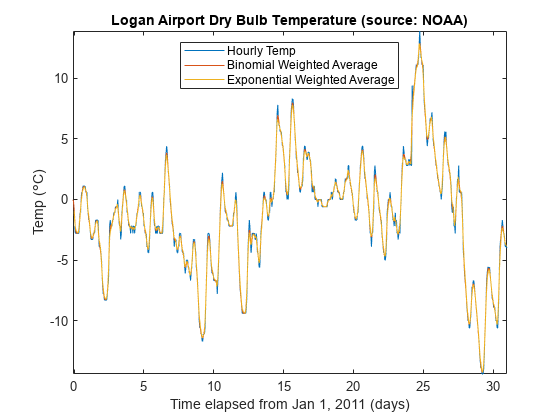
% 放大一天的读数。
axis([3 4 -5 2])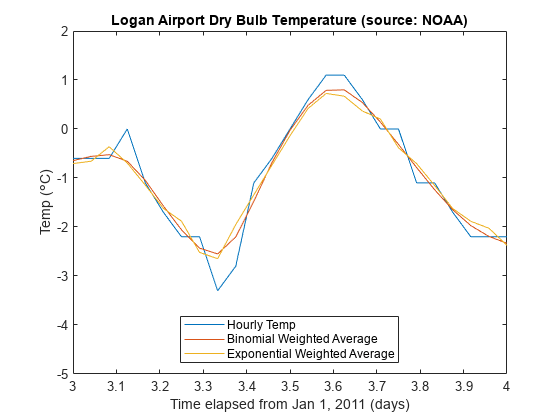
Savitzky-Golay 滤波器
您会注意到,通过平滑处理数据,极值得到一定程度的削减。
为了更紧密地跟踪信号,您可以使用加权移动平均滤波器,该滤波器尝试以最小二乘方式对指定数量的采样进行指定阶数的多项式拟合。
为了方便起见,您可以使用函数 sgolayfilt 来实现 Savitzky-Golay 平滑滤波器。要使用 sgolayfilt,请指定一个奇数长度段的数据和严格小于该段长度的多项式阶。sgolayfilt 函数在内部计算平滑多项式系数,执行延迟对齐,并处理数据记录开始和结束位置的瞬变效应。
cubicMA = sgolayfilt(tempC, 3, 7);
quarticMA = sgolayfilt(tempC, 4, 7);
quinticMA = sgolayfilt(tempC, 5, 9);
plot(days,[tempC cubicMA quarticMA quinticMA])
legend('Hourly Temp','Cubic-Weighted MA', 'Quartic-Weighted MA', ...
'Quintic-Weighted MA','location','southeast')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')
axis([3 5 -5 2])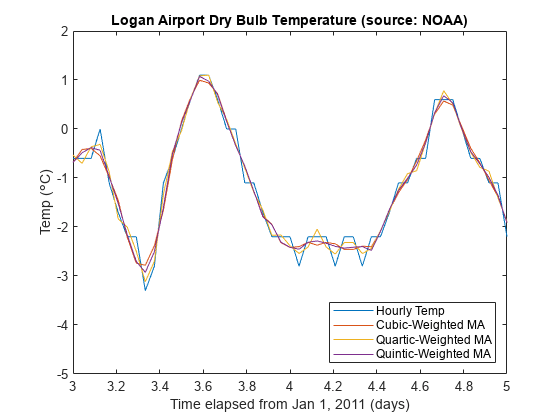
重采样
有时,为了正确应用移动平均值,对信号进行重采样是有益的。
在下一个示例中,我们对某模拟仪器输入端的开环电压进行采样,其中存在 60 Hz 交流电源线噪声的干扰。我们以 1 kHz 采样率对电压进行了采样。
load openloop60hertz
fs = 1000;
t = (0:numel(openLoopVoltage)-1) / fs;
plot(t,openLoopVoltage)
ylabel('Voltage (V)')
xlabel('Time (s)')
title('Open-loop Voltage Measurement')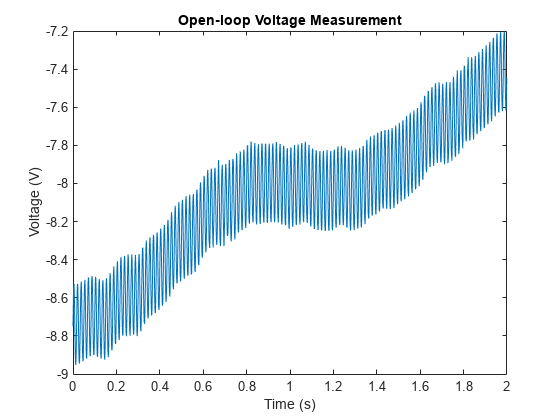
现在我们尝试通过使用移动平均滤波器来去除电源线噪声的影响。
如果您构造一个均匀加权的移动平均滤波器,它将去除相对于滤波器持续时间而言具有周期性的任何分量。
以 1000 Hz 采样时,在 60 Hz 的完整周期内,大约有 1000 / 60 = 16.667 个采样。我们尝试“向上舍入”并使用一个 17 点滤波器。这将在 1000 Hz / 17 = 58.82 Hz 的基频下为我们提供最大滤波效果。
plot(t,sgolayfilt(openLoopVoltage,1,17))
ylabel('Voltage (V)')
xlabel('Time (s)')
title('Open-loop Voltage Measurement')
legend('Moving average filter operating at 58.82 Hz', ...
'Location','southeast')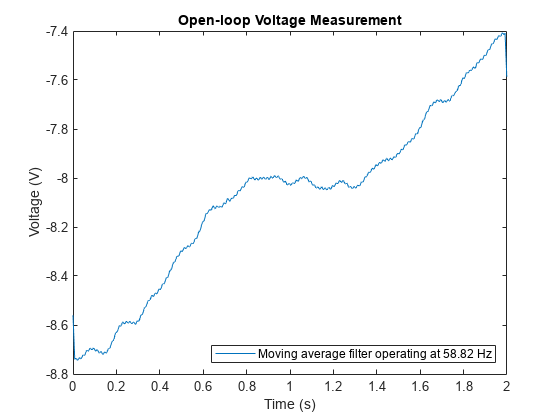
请注意,虽然电压明显经过平滑处理,但它仍然包含小的 60 Hz 波纹。
如果我们对信号进行重采样,以便通过移动平均滤波器捕获 60 Hz 信号的完整周期,就可以显著减弱该波纹。
如果我们以 17 * 60 Hz = 1020 Hz 对信号进行重采样,可以使用 17 点移动平均滤波器来去除 60 Hz 的电线噪声。
fsResamp = 1020;
vResamp = resample(openLoopVoltage, fsResamp, fs);
tResamp = (0:numel(vResamp)-1) / fsResamp;
vAvgResamp = sgolayfilt(vResamp,1,17);
plot(tResamp,vAvgResamp)
ylabel('Voltage (V)')
xlabel('Time (s)')
title('Open-loop Voltage Measurement')
legend('Moving average filter operating at 60 Hz', ...
'Location','southeast')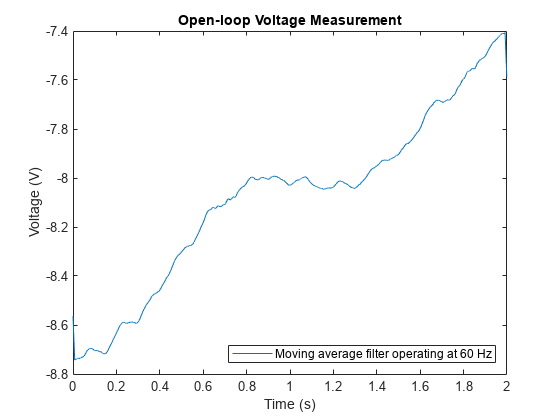
中位数滤波器
移动平均滤波器、加权移动平均滤波器和 Savitzky-Golay 滤波器对它们滤波的所有数据进行平滑处理。然而,有时我们并不需要这种处理。例如,如果我们的数据取自时钟信号并且不希望对其中的锐边进行平滑处理,该怎么办?到当前为止讨论的滤波器都不太适用:
load clockex
yMovingAverage = conv(x,ones(5,1)/5,'same');
ySavitzkyGolay = sgolayfilt(x,3,5);
plot(t,x, ...
t,yMovingAverage, ...
t,ySavitzkyGolay)
legend('original signal','moving average','Savitzky-Golay')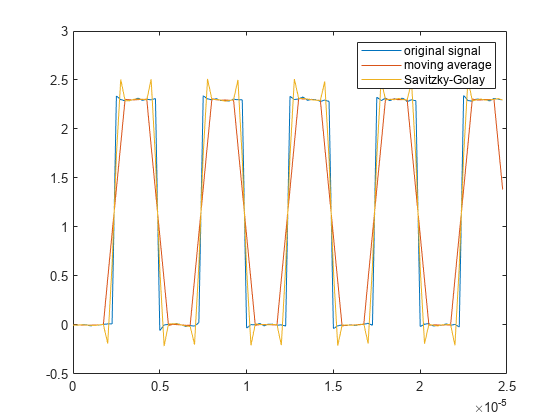
移动平均滤波器和 Savitzky-Golay 滤波器分别在时钟信号的边沿附近进行欠校正和过校正。
保留边沿但仍平滑处理水平的一种简单方法是使用中位数滤波器:
yMedFilt = medfilt1(x,5,'truncate');
plot(t,x, ...
t,yMedFilt)
legend('original signal','median filter')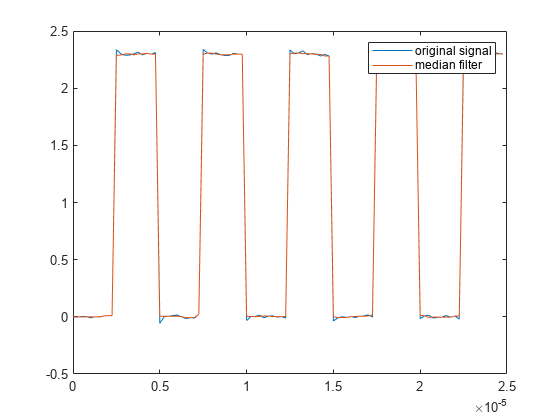
通过 Hampel 滤波器去除离群值
许多滤波器对离群值很敏感。与中位数滤波器密切相关的一种滤波器是 Hampel 滤波器。此滤波器有助于在不过度平滑处理数据的情况下去除信号中的离群值。
为了演示这一点,请加载一段火车鸣笛的录音,并添加一些人为噪声尖峰:
load train
y(1:400:end) = 2.1;
plot(y)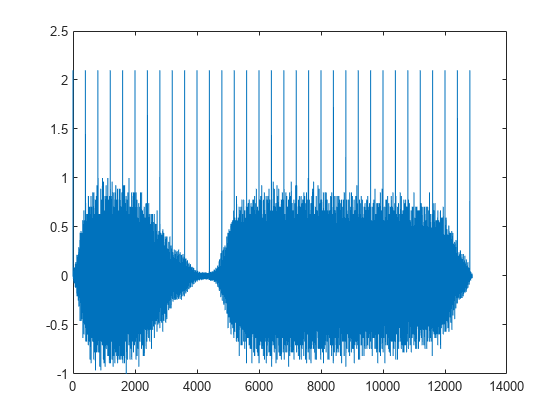
由于我们引入的每个尖峰只有一个采样的持续时间,我们可以使用只包含三个元素的中位数滤波器来去除尖峰。
hold on
plot(medfilt1(y,3))
hold off
legend('original signal','filtered signal')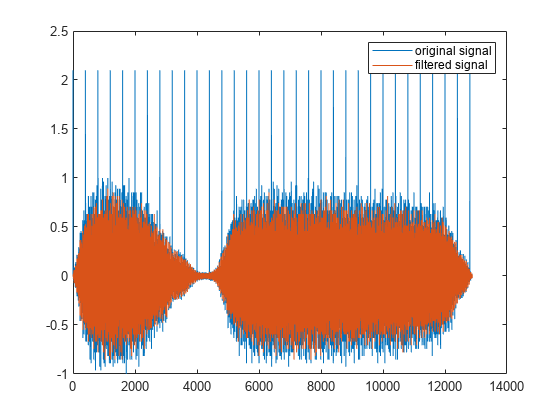
该滤波器去除了尖峰,但同时去除了原始信号的大量数据点。Hampel 滤波器的工作原理类似于中位数滤波器,但它仅替换与局部中位数值相差几倍标准差的值。
hampel(y,13)
legend('location','best')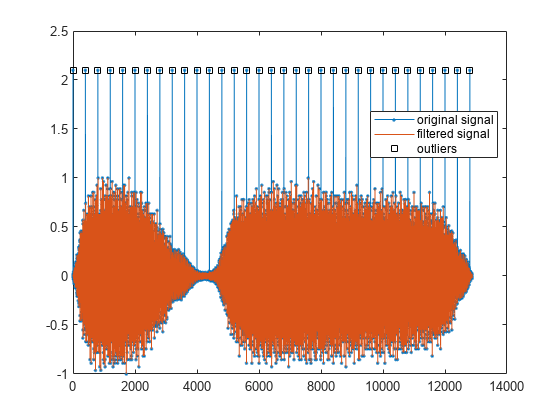
从原始信号中仅去除了离群值。
【我是小蜜蜂,知识的搬运工!】