前话：分析试验数据的差异，一般都会假设样本值之间或者样本与标准值之间无差异，根据不同方法计算得出的t值、q值、F值等等，均表示两者之间的差异程度，值越大，两者差异越大，该假设越不成立，而SAS中的Pr>|t|指的则是原假设成立的概率。（即两者无差异的概率，显著性水平一般以0.05与0.01作为判断标准，若小于0.05，这表示差异显著，小于0.01表示差异极显著）

t检验分为单个样本平均数的假设检验、非配对样本t检验与配对样本t检验3种。

1.单个样本平均数的假设检验

该检验通过检验一个样本所在的总体平均数与已知的总体平均数是否相同，来判断某样本是否来源于某一总体。

例1，已知母猪孕期为114天，抽检10头母猪的怀孕期为116,115,113,112,114,117,115,116,114,113（d），试判断该样本所在的总体平均数与114是否存在差异：

data pig;
input a@@;
x=114-a;
cards;
116 115 113 112 114 117 115 116 114 113
;
proc means n mean stderr t prt;
var x;
run;

结果为：

上图看出pr>|t|处，p值为34.34%，即意味着，抽取的10头样本猪孕期与标准值114天，两者一致的可能性达到34.34%，因此认为其无统计学差异。【该值只有低于0.05（5%），才能认为不到5%的把握认为两者一致，即95%以上的把握认为两者不同，存在统计学差异】

例2：按饲料配方要求，每1000kg饲料中维生素C含量应高于246g，从某厂生产的饲料中随机抽测12个样品，测得其维生素C的含量如下：255,260,262,248,244,245,250,238,246,248,258,270。若饲料中维生素C含量服从正态分布，则该厂生产饲料是否符合要求？

注：需一尾t检验。

2.非配对样本t检验

两样本相互独立，含量不一定相同，但处理一样。可用于检验两样本所在总体的平均数是否一致。

例3：长白12头，蓝塘11头，设两种猪90kg时背膘厚度服从正态分布且方差相等，判断2种后背猪90kg时的背膘厚度有无差异。

长白	1.2	1.32	1.1	1.28	1.35	1.08	1.18	1.25	1.3	1.12	1.19	1.05
蓝塘	2	1.85	1.6	1.78	1.96	1.88	1.82	1.7	1.68	1.92	1.8

data B;
input breed y@@;
cards;
1 1.20 1 1.32 1 1.10 1 1.28 1 1.35 1 1.08 1 1.18 1 1.25
1 1.30 1 1.12 1 1.19 1 1.05 2 2.00 2 1.85 2 1.60 2 1.78
2 1.96 2 1.88 2 1.82 2 1.70 2 1.68 2 1.92 2 1.80
;
proc Ttest;
class breed;
var y;
run;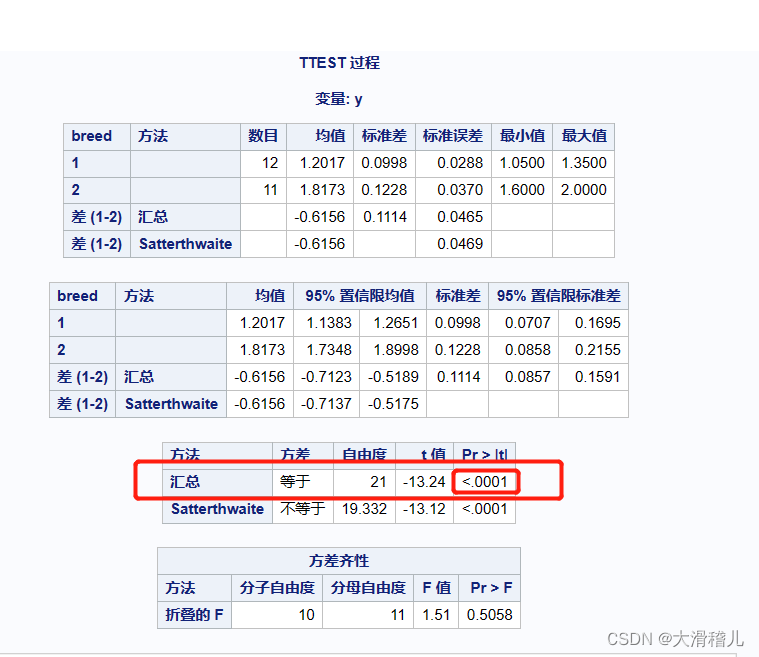

p<0.01，差异极显著， 故2种后背猪90kg时的背膘厚度差异极其显著。

3.配对样本t检验

配对样本要求试验单位初始条件尽可能一致，两组数据数量一定对等。其可减少系统误差，降低实验误差，提高试验精确性与准确性，采用局部控制原则，可分为自身配对、同源配对。

例4：用家兔10只测试某匹注射液对体温的影响，测定每只家兔注射前后的体温，若体温服从正态分布，则问家兔注射该注射液前后体温有无差异？

注射前	37.8	38.2	38	37.6	37.9	38.1	38.2	37.5	38.5	37.9
注射后	37.9	39	38.9	38.4	37.9	39	39.5	38.6	38.8	39

data rabbit;
input a b c@@;
d=b-c;
cards;
1 37.8 37.9 2 38.2 39.0 3 38.0 38.9 4 37.6 38.4
5 37.9 37.9 6 38.1 39.0 7 38.2 39.5 8 37.5 38.6
9 38.5 38.8 10 37.9 39.0
;
proc means mean strerr t prt;
var d;
run;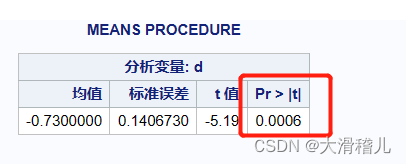

p<0.05,差异明显。