目录
6.1.概述
6.2.AVL树
6.2.1.概述
6.2.2.旋转
1.RR旋转
2.LL旋转
3.LR旋转
4.RL旋转
6.2.3.代码实现
6.1.概述
二叉搜索树存在一个问题,就是树的姿态和数据的插入顺序是有关系的,有时候树会变成某一边的子树高度过高,甚至直接退化成斜二叉树,使得查找从二分查找跌落为顺序查找:
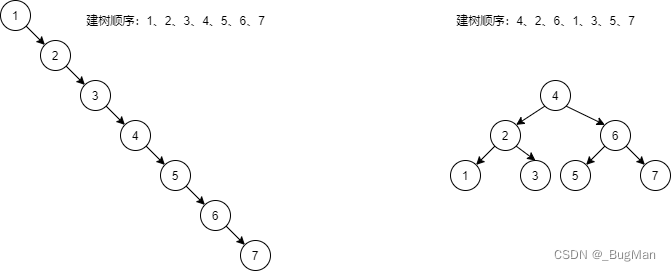
保证任意结点左右子树的高度一致,便可以保证树的查询效率为最优,但是此种情况过于理想,难以达到,因此允许左右子树的高度间存在差异,于是出现了平衡二叉树,即任意结点左右子树高度差不超过1:
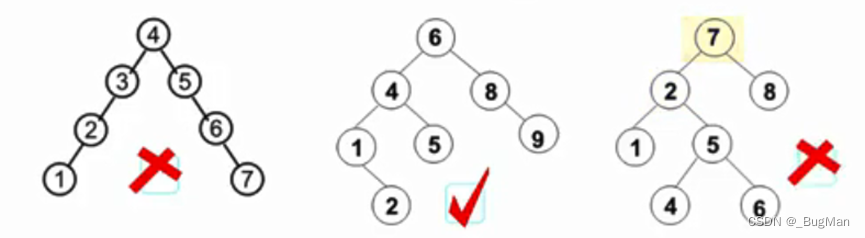
每次操作后出现有结点的左右子树高度差超过1的情况时,树会自己进行调整姿态,重新达到平衡。
平衡二叉树只是一种思想,有很多种实现,常见的实现有红黑树、AVL、Treap、伸展树等。
6.2.AVL树
6.2.1.概述
AVL是出现的第一种平衡二叉树,每当插入元素,造成AVL树的不平衡后,它会通过旋转的方式调整最小不平衡树,从而将树调整平衡。插入后造成不平衡的元素叫“破坏者”,最小不平衡树的根节点叫“被破坏者”。
最小不平衡树,即从高度差超过1的两条分支开始向上找,找到它们的第一个共同父结点,以这个父节点为根结点的子树就是最小不平衡树。
AVL的旋转有四种:
- RR旋转
- LL旋转
- LR旋转
- RL旋转
6.2.2.旋转
1.RR旋转
“破坏者”在右子树的右子树,执行RR旋转,将“被破坏者”的右孩子提为根节点,该右孩子的左子树移植为“被破坏者”的右子树。

2.LL旋转
“破坏者”在左子树的左子树,就执行LL旋转,将“被破坏者”压为“破坏者”父节点的右孩子,“破坏者”父节点往上走一层。

3.LR旋转
破坏者在左子树的右子树,就执行LR旋转,步骤和LL旋转相同,将“被破坏者”压为“破坏者”父节点的右孩子,“破坏者”父节点往上走一层。
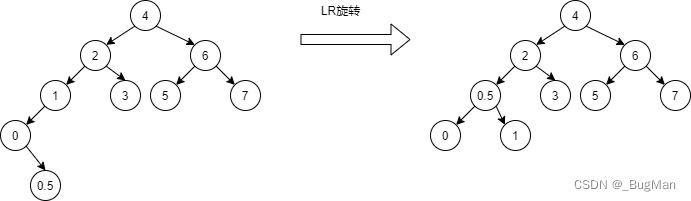
4.RL旋转
破坏者在右子树的左子树执行RL旋转,调整被破坏者,被破坏者的R,以及被破坏者R的L(这里可能有点晕,其实仔细观察会发现其实就是契合右子树的左子树这个位置关系。),被破坏者的R提上,被破坏者的R的L不变。

6.2.3.代码实现
public class AvlTree<T extends Comparable<? super T>> {
private AvlNode<T> root;
public void insert(T x) {
root = insert(x, root);
}
public void remove(T x) {
root = remove(x, root);
}
public T findMin() {
return findMin(root).element;
}
public void makeEmpty() {
root = null;
}
public boolean isEmpty() {
return root == null;
}
/**
* 添加节点
*
* @param x 插入节点
* @param t 父节点
*/
private AvlNode<T> insert(T x, AvlNode<T> t) {
//如果根节点为空,则当前x节点为根及诶单
if (null == t) {
return new AvlNode(x);
}
int compareResult = x.compareTo(t.element);
//小于当前根节点 将x插入根节点的左边
if (compareResult < 0) {
t.left = insert(x, t.left);
} else if (compareResult > 0) {
//大于当前根节点 将x插入根节点的右边
t.right = insert(x, t.right);
} else {
}
return balance(t);
}
private static final int ALLOWED_IMBALANCE = 1;
private AvlNode<T> balance(AvlNode<T> t) {
if (t == null) {
return t;
}
if (height(t.left) - height(t.right) > ALLOWED_IMBALANCE) {
if (height(t.left.left) >= height(t.left.right)) {
t = rotateWithLeftChild(t);
} else {
t = doubleWithLeftChild(t);
}
} else if (height(t.right) - height(t.left) > ALLOWED_IMBALANCE) {
if (height(t.right.right) >= height(t.right.left)) {
t = rotateWithRightChild(t);
} else {
t = doubleWithRightChild(t);
}
}
t.height = Math.max(height(t.left), height(t.right)) + 1;
return t;
}
private AvlNode<T> doubleWithRightChild(AvlNode<T> k3) {
k3.right = rotateWithLeftChild(k3.right);
return rotateWithRightChild(k3);
}
private AvlNode<T> rotateWithRightChild(AvlNode<T> k2) {
AvlNode k1 = k2.right;
k2.right = k1.left;
k1.left = k2;
k2.height = Math.max(height(k2.right), height(k2.left)) + 1;
k1.height = Math.max(height(k1.right), k2.height) + 1;
return k1;
}
private AvlNode<T> doubleWithLeftChild(AvlNode<T> k3) {
k3.left = rotateWithRightChild(k3.left);
return rotateWithLeftChild(k3);
}
private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2) {
AvlNode k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
k1.height = Math.max(height(k1.left), k2.height) + 1;
return k1;
}
private int height(AvlNode<T> t) {
return t == null ? -1 : t.height;
}
/**
* 删除节点
*
* @param x 节点
* @param t 父节点
*/
private AvlNode<T> remove(T x, AvlNode<T> t) {
if (null == t) {
return t;
}
int compareResult = x.compareTo(t.element);
//小于当前根节点
if (compareResult < 0) {
t.left = remove(x, t.left);
} else if (compareResult > 0) {
//大于当前根节点
t.right = remove(x, t.right);
} else if (t.left != null && t.right != null) {
//找到右边最小的节点
t.element = findMin(t.right).element;
//当前节点的右边等于原节点右边删除已经被选为的替代节点
t.right = remove(t.element, t.right);
} else {
t = (t.left != null) ? t.left : t.right;
}
return balance(t);
}
/**
* 找最小节点
*
* @param root 根节点
*/
private AvlNode<T> findMin(AvlNode<T> root) {
if (root == null) {
return null;
} else if (root.left == null) {
return root;
}
return findMin(root.left);
}
/**
* 找最大节点
*
* @param root 根节点
*/
private AvlNode<T> findMax(AvlNode<T> root) {
if (root == null) {
return null;
} else if (root.right == null) {
return root;
} else {
return findMax(root.right);
}
}
public void printTree() {
if (isEmpty()) {
System.out.println("节点为空");
} else {
printTree(root);
}
}
public void printTree(AvlNode<T> root) {
if (root != null) {
System.out.print(root.element);
if (null != root.left) {
System.out.print("左边节点" + root.left.element);
}
if (null != root.right) {
System.out.print("右边节点" + root.right.element);
}
System.out.println();
printTree(root.left);
printTree(root.right);
}
}
}