一、什么是计数排序？

计数排序，是通过统计每一个数字出现的次数，并把它映射到与它自己本身数值相同的下标处，再遍历映射的数组使原数组有序的一种排序方法，计数排序的本质是一种哈希算法，也就是通过建立映射关系来达到排序的目的。

二、如何实现计数排序？

基本思路：先开辟一个映射数组，然后遍历原数组，数组中的元素是几就在开辟的的映射数组下标为几的位置+1。得到的这个映射数组就包含了原数组中所有元素的映射关系。遍历一遍映射数组找出原数组中出现过的数即可。

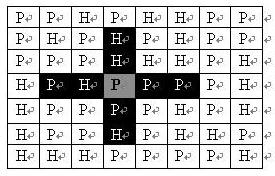
演示图如下：


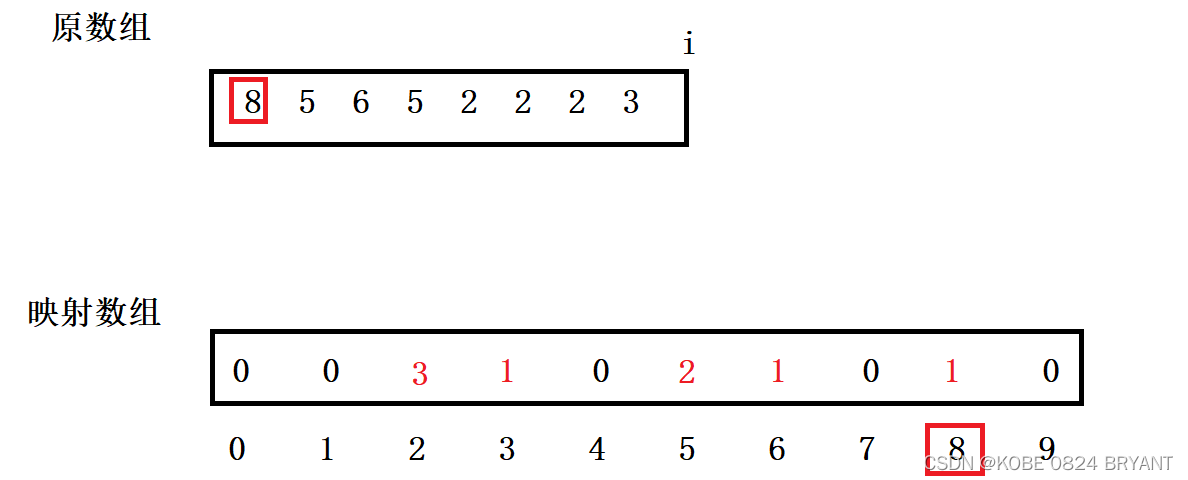
观察可以知道，映射数组中每个位置对应的值代表这个下标的值在原数组中出现了多少次，那么我们看上图可以知道2出现了3次，3出现了1次，5出现看2次，6出现了1次，8出现了1次，其它出现了0次。那么我们遍历一遍映射数组并把对应的值放回到原数组就完成了排序了。
但是这里面临着一个问题，那就是我们开辟的数组到底要开多大的空间呢？显然，我们在上述例子中开辟了10个整形空间的数组，但是可以看到，有5个位置都是空的，也就是说有五个位置的数都是没出现过的，这样子开辟空间显然是有些浪费了，我们上面的写法是一种绝对映射的写法，绝对映射就是这个数本身是多少就映射到下标为多少的位置，但是如果我给出以下这个数组让你排序呢？

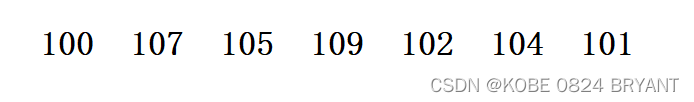
显然，以上数字的最大值是109，也就是说如果用绝对映射的方法那我们至少需要开110个空间，因为109要映射到下标为109的位置，下标从0开始，0-109就是110个数。但是仔细观察你会发现，这些数都是在100-109之间的，换句话说如果你开辟110个空间，那么前100个位置都是0，没有数映射，所以就等于是白白浪费了100个整形的空间，这显然是不能接受的，所以有人就想出来了一种相对映射的方法，我的100映射到0的位置，我的109映射到9的位置，其它的也以此类推，每个数在映射的时候都减去100，等到取出数据的时候在加上100就能得到原来的数了。这样一来，我们需要开10个整形的空间就可以了，大大减少了内存的消耗。
那我们应该开多大的空间呢？
开辟的空间的大小=最大元素-最小元素+1
例如上面的例子就是：开辟空间的大小=109-100+1=10
为什么要+1？因为数组下标是从0开始的，如果不+1，那就是开辟9个空间，那么109就没法映射到109-100=9的位置了。

参考代码如下：

void CountSort(int* a, int n)
{
	assert(a);
	int i = 0;
	int max = a[0];
	int min = a[0];
	//找出最大最小值，算出需要开辟多大的空间
	for (i = 1; i < n; i++)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	//需要开辟的空间的大小range
	int range = max - min + 1;
	int* CountArr = (int*)malloc(sizeof(int) * range);
	if (CountArr == NULL)
	{
		perror(" ");
		return;
	}
	//一定要先初始化为0，不然的话是随机数就会影响统计的结果
	memset(CountArr, 0, sizeof(int) * range);
	//遍历数组，给映射数组对应的位置统计数组出现的次数
	for (i = 0; i < n; i++)
	{
		//减去min是它的相对映射的位置
		CountArr[a[i] - min]++;
	}

	//遍历映射数组
	int j = 0;
	for (i = 0; i < range; i++)
	{
		//对应的位置是几就把这个数字往原数组中填几次
		while (CountArr[i]--)
		{
			//由于上面在映射的时候减去了min，所以在重新
			//写回数组的时候需要加上min得到原来的值
			a[j++] = i + min;
		}
	}

	free(CountArr);
	CountArr = NULL;
}

三、适用场景

尽管相对映射能处理一些相对集中的元素的排序的问题，但也只是解决了相对较为集中的元素的排序的问题，如果一个数组的数是很分散的，例如：1，100，102，104，那这个相对映射方法依然没办法很好地减少内存的消耗，所以计数排序是具有局限性的，只适合元素相对较为集中的数组的排序，而且只能排整数，不能排其他类型的数据，如浮点数等等。因为下标只能是整数。对于相对映射是可以对负数进行排序的，因为无论如何最小的那个元素都是映射到0的位置的，不会越界，但是绝对映射不能对负数排序，不然的话下标访问负数就一定会越界访问的。所以计数排序的使用场景还是很局限的。

四、时间复杂度和空间复杂度

毫无疑问，时间复杂度是O(N)就能解决问题的，因为只遍历了两次数组。空间复杂度是O(range)，如果N（元素个数）远远大于range，那么可以认为是O(1)的，如果N和range是同一数量级的，那么是O(N)，如果range远远大于N，那么是O(range)。
在适当的场景下，计数排序的时间复杂度比其它的所有排序的时间复杂度都要低，可以认为是O(N)的，但是由于有很大的局限性，所以在很多地方都不适用。计数排序也就得不到推广。

以上就是计数排序的全部内容，你学会了吗？如果对你有所帮助，那就点亮一下小心心，顺便点点关注呗！我们下期见！！！