215. 数组中的第K个最大元素

题目

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

解题思路

读完题目，不难看出这道题需要我们先对原数组进行排序。并且排序算法的时间复杂度需要为$O(n)$。（第一次用时间复杂度为$O(n^2)$的插入排序算法时，因为超出时间限制不通过。）然后抱着试一试的心态，调用Python内置的sorted函数直接解决了。

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        return sorted(nums)[-k]

解题思路【学习】

当然，这道算法题目的目的肯定不是让我们学会如何调api解决问题。翻看了一下题解，发现需要用到快速排序或者堆排序才能满足题目的时间复杂度要求。

各种排序算法的时间空间复杂度如下：各种排序算法的时间空间复杂度_排序算法时间复杂度_方tongxue的博客-CSDN博客

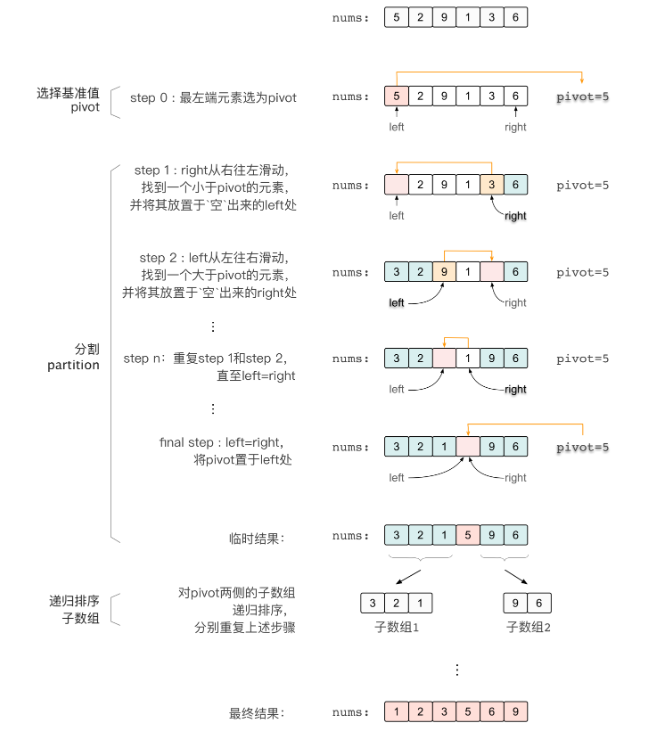
基于快速排序的选择方法

参考原文：『 TopK问题 』快速排序、堆排序详解 - 数组中的第K个最大元素 - 力扣（LeetCode）

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        import random

        def partition(nums, left, right):
            pivot = nums[left]  # 选择一个基准值（最左端元素）
            i, j = left, right  # 双指针
            while i < j:
                while i < j and nums[j] >= pivot:  # 从右往左查找，直到找到一个比pivot更小的数
                    j -= 1
                nums[i] = nums[j]  # 将更小的数放入左边
                while i < j and nums[i] <= pivot:  # 从左往右查找，直到找到一个比pivot更大的数
                    i += 1
                nums[j] = nums[i]  # 将更大的数放入右边
            # 循环结束，i与j相等
            nums[i] = pivot  # 待比较数据放入最终位置
            return i  # 返回基准值最终位置

        def randomPartition(nums, left, right):
            pivot_idx = random.randint(left, right)  # 随机选择pivot
            nums[left], nums[pivot_idx] = nums[pivot_idx], nums[left]  # pivot放置到最左边
            return partition(nums, left, right)  # 调用partition函数

        def topk_split(nums, k, left, right):
            # 寻找到第k个数停止递归，使得nums数组中index左边是前k个小的数，index右边是后面n-k个大的数
            if left < right:
                index = randomPartition(nums, left, right)
                # index = partition(nums, left, right)
                if index == k:
                    return
                elif index < k:
                    topk_split(nums, k, index + 1, right)
                else:
                    topk_split(nums, k, left, index - 1)
        
        # 获得第k大的数
        def topk_large(nums, k):
            # parttion是按从小到大划分的，如果让index左边为前n-k个小的数，则index右边为前k个大的数
            topk_split(nums, len(nums) - k, 0, len(nums) - 1)  # 把k换成len(nums)-k
            return nums[len(nums) - k]

        return topk_large(nums,k)