多项式回归
概念
线性回归研究的是一个因变量与一个自变量之间的回归问题。
多项式回归是指在线性回归的基础上，通过增加非线性特征来拟合非线性数据的方法。多项式回归模型可以用一个 n 次多项式函数来近似描述目标变量和输入变量之间的关系。例如，对于只有一个自变量
x 的情况，可以将拟合函数写作：
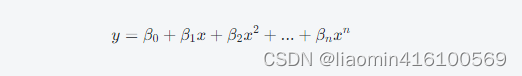
其中
y 表示目标变量，x 表示自变量，
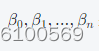是模型的参数。模型的目标是通过调整参数来使预测值与真实值的误差最小化。
多项式回归可以通过 Scikit-Learn 的 PolynomialFeatures 类来实现，它可以将原始的自变量数据转化为包含了多项式特征的新自变量数据。这样，我们就可以使用线性回归算法来处理增广后的非线性特征，从而得到多项式回归模型。
拟合实例
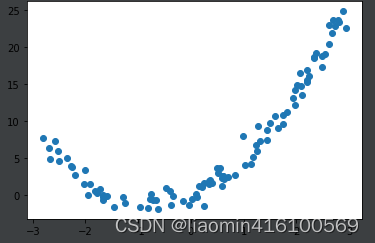
生成一个多项式的模拟数据 y=3x+2x**2
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 3*x+ 2*x**2+ np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()
如果直接使用线性回归，看一下效果：
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()
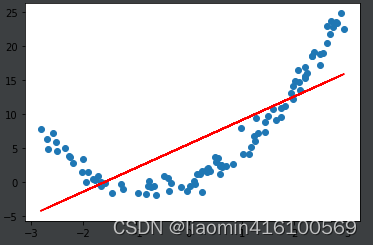
很显然，拟合效果并不好。那么解决呢？
解决方案：添加一个特征。 x**2
X2 = np.hstack([X, X**2])
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()
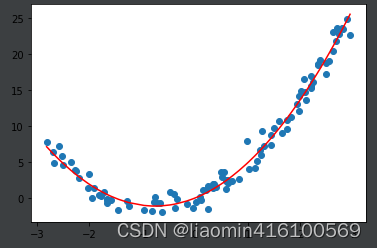
这样就比直线拟合要好很多,斜率和截距是。
[2.9391452 1.94366894]
0.04332751905483523
scikit-learn中的多项式回归
polynomialFeatures
polynomialFeatures是Scikit-Learn中的一个函数，用于将输入数据转化为多项式特征集合。其作用是在对非线性数据进行线性回归时，通过增加非线性特征来拟合非线性数据。
具体地，PolynomialFeatures函数将原始的特征向量转化为包含了所有多项式组合的新特征向量。例如，如果原始特征向量为 [a,b]，且使用degree=2，那么通过PolynomialFeatures生成的新特征向量为 [1,a,b,a^2, ab,b^2]。如果原始特征向量为 [x]，且使用degree=2，那么通过PolynomialFeatures生成的新特征向量为 [1,x,x^2]
这样，由于新特征向量包含了原始特征向量的所有多项式，可以更好地拟合非线性函数。
PolynomialFeatures主要有以下参数：
- degree：表示多项式的次数，决定了到多少次项的多项式将被生成。
- interaction_only：默认为False，表示新特征向量包含交叉项和高次项，如a×b、a^2等等。
- include_bias：默认为True，表示是否创建偏差列。
总之，PolynomialFeatures是一个非常有用的函数，可以帮助我们更好地处理非线性数据，从而提高模型的预测能力。
from sklearn.preprocessing import PolynomialFeatures
# 这个degree表示我们使用多少次幂的多项式
poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)
print(X2.shape)
print(X2)
输出结果(第一列是常量1，第二列是之前的x，第三列是x**2)：
(100, 3)
[[ 1.00000000e+00 -2.37462045e+00 5.63882230e+00]
[ 1.00000000e+00 -7.90962247e-01 6.25621276e-01]
[ 1.00000000e+00 -7.02888543e-01 4.94052304e-01]
[ 1.00000000e+00 -6.54589498e-01 4.28487411e-01]]
使用线性回归拟合
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(X2, y)
y_predict = reg.predict(X2)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()
print(lin_reg2.coef_)
# array([0.90802935, 1.04112467])
print(lin_reg2.intercept_)
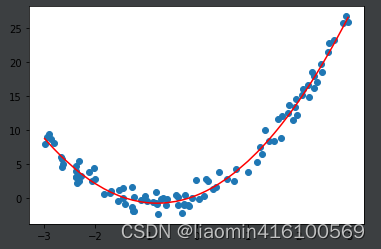
输出截距和斜率
[3.02468873 1.94228967]
0.41539122650325755
之前使用的都是1维数据，如果使用2维3维甚至更高维呢？
生成一个二维数据（1到10，转换为5行2列）
import numpy as np
x = np.arange(1, 11).reshape(5, 2)
print(x)
输出
[[ 1 2]
[ 3 4]
[ 5 6]
[ 7 8]
[ 9 10]]
使用PolynomialFeatures构造
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures()
poly.fit(x)
x2 = poly.transform(x)
print(x2)
输出
[[ 1. 1. 2. 1. 2. 4.]
[ 1. 3. 4. 9. 12. 16.]
[ 1. 5. 6. 25. 30. 36.]
[ 1. 7. 8. 49. 56. 64.]
[ 1. 9. 10. 81. 90. 100.]]
此时，可以看出当数据维度是2维是，经过多项式预处理生成了6维数据，第一列很显然是0次项系数，第二列和第三列也很好理解，分别是x1，x2，第四列和第六列分别是 x12和x22 ,还有一列，其实是x1*x2,这就是第5列，总共6列。由此可以猜想一下如果数据是3维的时候是什么情况？
poly = PolynomialFeatures(degree=3)
poly.fit(x)
x3 = poly.transform(x)
print(x3)
输出
[[ 1. 1. 2. 1. 2. 4. 1. 2. 4. 8.]
[ 1. 3. 4. 9. 12. 16. 27. 36. 48. 64.]
[ 1. 5. 6. 25. 30. 36. 125. 150. 180. 216.]
[ 1. 7. 8. 49. 56. 64. 343. 392. 448. 512.]
[ 1. 9. 10. 81. 90. 100. 729. 810. 900. 1000.]]
那么这10列，分别对应着什么？通过PolynomiaFeatures，将所有的可能组合，升维的方式呈指数型增长。这也会带来一定的问题。 如何解决这种爆炸式的增长？如果不控制一下，试想x和x[^100]相比差异就太大了。这就是传说中的过拟合。
sklearn中的Pipeline
sklearn中的Pipeline是一个工具，可以将多个数据预处理步骤（transformer）和一个机器学习模型（estimator）串联在一起，形成一个完整的机器学习流程。Pipeline 中的每个步骤都是一个包含 fit 和 transform 方法的对象，其中 fit 方法用于拟合训练数据，transform 方法用于对数据进行转换。
通过 Pipeline 可以将多个预处理算法和机器学习算法组合在一起，使得整个流程变得规范化和简化，同时可以方便地进行交叉验证和参数调节等操作。Pipeline 中的每个步骤都可以使用一个字符串来标识，这个字符串可以用于对模型中的超参数进行调节。
Pipeline 通常用于机器学习中的特征工程，在数据预处理的过程中构建完整的机器学习流程，并将其应用于训练集和测试集中。通过将多个步骤组合在一起，避免了手动地进行特征工程和模型选择的各种组合操作，同时也提高了代码复用性和可维护性。
一般情况下多项式回归，我们会对数据进行归一化，然后进行多项式升维，再接着进行线性回归。因为sklearn中并没有对多项式回归进行封装，不过可以使用Pipeline对这些操作进行整合。
#%%
import numpy as np
import matplotlib.pyplot as plt
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 3*x+ 2*x**2+ np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()
#%%
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
poly_reg = Pipeline([
('poly', PolynomialFeatures(degree=2)),
('std_scale', StandardScaler()),
('lin_reg', LinearRegression())
])
poly_reg.fit(X, y)
y_predict = poly_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
过拟合和欠拟合
多项式回归的最大优点就是可以通过增加x的高次项对实测点进行逼近，直至满意为止。但是这也正是它最大的缺点，因为通常情况下试过过高的维度对数据进行拟合，在训练集上会有很好的表现，但是测试集可能就不那么理想了，这也正是解决过拟合的一种办法。
均方误差
mean_squared_error 是一个用于计算两个数组之间均方误差（Mean Squared Error，简称MSE）的函数。它是评价回归模型准确度的一种常见指标。
该函数的输入参数包括：
- y_true: 真实值数组；
- y_pred: 预测值数组；
- sample_weight: 用于对样本赋权重的数组，可以不传入，默认值为 None
函数返回的是一个数值，表示两个数组之间的均方误差。
均方误差是回归模型中使用广泛的一种衡量模型预测能力的指标。均方误差越小说明模型的预测越准确。它的定义是：将每个样本预测值与真实值之间的偏差进行平方后求和，再除以样本总数得到的平均值，即
均方误差越小就意味着模型的预测能力越准确
拟合效果
以下使用同一个方式生成数据集之后，使用不同的拟合方式，并使用均方误差来对比几种拟合的效果。
线性拟合
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
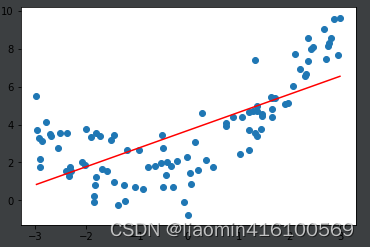
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
print("线性均方误差",mean_squared_error(y, y_predict))
输出：3.0750025765636577
显然，直接使用简单的一次线性回归，拟合的结果就是欠拟合(underfiting)，
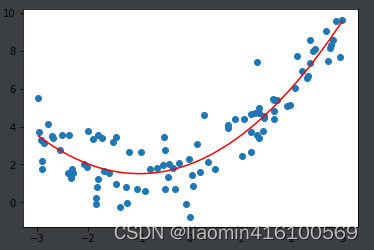
二次多项式拟合
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
def PolynomialRegression(degree):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scale', StandardScaler()),
('lin_reg', LinearRegression())
])
poly_reg = PolynomialRegression(degree=2)
poly_reg.fit(X, y)
Pipeline(memory=None,
steps=[('poly', PolynomialFeatures(degree=2, include_bias=True, interaction_only=False)), ('std_scale', StandardScaler(copy=True, with_mean=True, with_std=True)), ('lin_reg', LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
normalize=False))])
y_predict = poly_reg.predict(X)
print("2次多项式均方误差",mean_squared_error(y, y_predict))
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
输出：1.0987392142417856
二次多项式回归的拟合程度要高于线性回归。
十次多项式拟合
poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(X, y)
y10_predict = poly10_reg.predict(X)
print("10次多项式均方误差",mean_squared_error(y, y10_predict))
plt.scatter(x, y)
plt.plot(np.sort(x), y10_predict[np.argsort(x)], color='r')
plt.show()
输出：1.0508466763764202
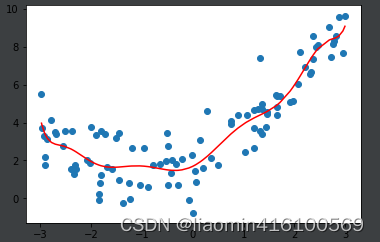
百次多项式拟合
poly10_reg = PolynomialRegression(degree=100)
poly10_reg.fit(X, y)
y10_predict = poly10_reg.predict(X)
print("100次多项式均方误差",mean_squared_error(y, y10_predict))
plt.scatter(x, y)
plt.plot(np.sort(x), y10_predict[np.argsort(x)], color='r')
plt.show()
输出：0.6870911922673567
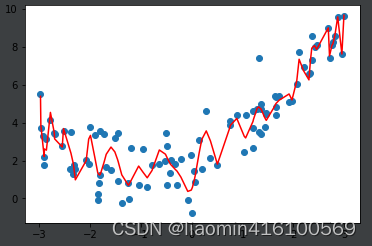
百次多项式生成数据集测试
从上面的图形看出uniform生成的数据预测的y值都在-1到10之间，我们使用相同的模型预测下 x=3的值
y_plot = poly100_reg.predict([[3]])
print(y_plot)
输出：[-2.49133715e+06 -6.32965634e+24]
转换下：-2.49133715e+06==-2491337.16790313
发现>=3后，如果按照这个弯月形的图形，明显是不正常的。
我们生成一个等差数列作为测试集
from sklearn.preprocessing import PolynomialFeatures
x_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly100_reg.predict(x_plot)
plt.scatter(x, y)
plt.plot(x_plot[:,0], y_plot, color='r')
# plt.axis([-3, 3, -1, 10])
plt.show()
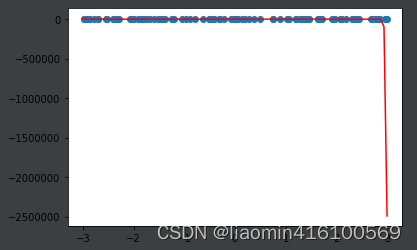
这样因为x=3图形都乱了，我们截图图形x从-3到3 y从-1到10
from sklearn.preprocessing import PolynomialFeatures
x_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly100_reg.predict(x_plot)
plt.scatter(x, y)
plt.plot(x_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, -1, 10])
plt.show()
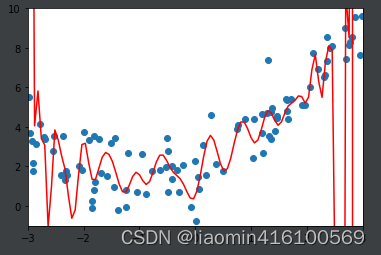
说明通过训练集训练出的模型对测试集没有很好的表现能力
解决过拟合问题
通常在机器学习的过程中，主要解决的都是过拟合问题，因为这牵涉到模型的泛化能力。所谓泛化能力，就是模型在验证训练集之外的数据时能够给出很好的解答。只是对训练集的数据拟合的有多好是没有意义的，我们需要的模型的泛化能力有多好。
为什么要训练数据集与测试数据集？
通常情况下我们会将数据集分为训练集和测试集，通过训练数据训练出来的模型如果能对测试集具有较好的表现，才有意义。
以下使用train_test_split将生成的数据拆分为训练集和测试集，重新生成模型并计算均方误差
使用线性回归
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
x_train, x_test, y_train, y_test = train_test_split(X, y, random_state=666)
lin_reg = LinearRegression()
lin_reg.fit(x_train, y_train)
y_predict = lin_reg.predict(x_test)
mean_squared_error(y_test, y_predict)
输出结果：2.2199965269396573
使用二项式
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
def PolynomialRegression(degree):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scale', StandardScaler()),
('lin_reg', LinearRegression())
])
poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(x_train, y_train)
y2_predict = poly2_reg.predict(x_test)
mean_squared_error(y_test, y2_predict)
输出结果： 0.8035641056297901
使用10项式
poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(x_train, y_train)
y10_predict = poly10_reg.predict(x_test)
mean_squared_error(y_test, y10_predict)
输出结果：0.9212930722150781
通过上面的例子可以发现，当degree=2的时候在测试集上的均方误差和直线拟合相比好了很多，但是当degree=10的时候再测试集上的均方误差相对degree=2的时候效果差了很多，这就说名训练出来的模型已经过拟合了。
100项式
poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(x_train, y_train)
y100_predict = poly100_reg.predict(x_test)
mean_squared_error(y_test, y100_predict)
输出结果：14440175276.314638
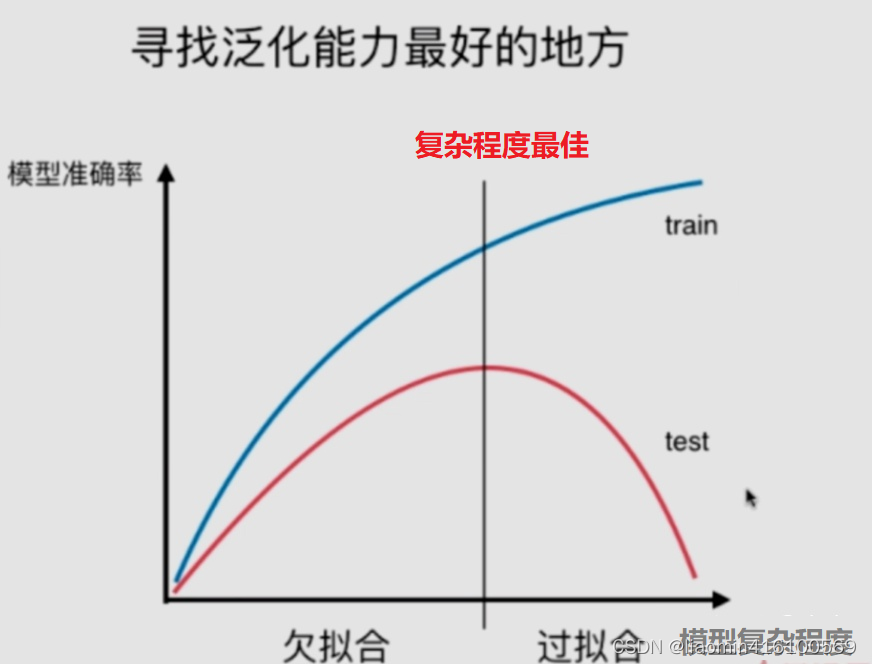
小结：对于模型复杂度与模型准确率中寻找泛化能力最好的地方。
- 欠拟合：underfitting，算法所训练的模型不能完整表述数据关系。
- 过拟合：overfitting，算法所训练的模型过多地表达数据间的噪音关系。
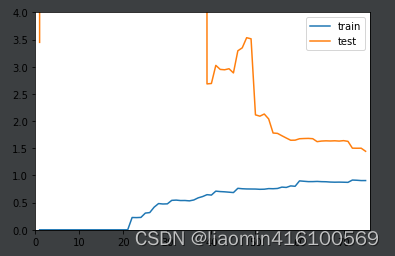
学习曲线
机器学习的学习曲线是一种图形化表示机器学习算法在训练数据上表现的方式，通常以训练数据集大小或训练迭代次数为横轴，以模型性能指标（如准确率、误差等）为纵轴。这条曲线可以帮助我们了解算法的学习过程，评估学习效果和调整模型。
随着训练数据集的增加，我们希望看到模型的性能不断提高；而如果在训练集上性能较好但在测试集上表现欠佳，则说明出现了过拟合（overfitting）问题；相反，如果在训练集和测试集上的表现都不好，则可能需要重新考虑数据预处理、特征工程和模型结构等问题。
与学习曲线相关的概念还包括偏差（bias）和方差（variance），它们通常被用来对模型进行诊断和调整。当模型的偏差较大时，说明模型太简单，不能准确地拟合训练集和测试集，需要增加模型复杂度；而当模型的方差较大时，说明模型过于复杂，出现了过拟合问题，需要缩减模型复杂度或增加训练数据集的大小。
我们尝试将整个数据集拆分为训练集和测试机，训练集的大小从1到len（训练集）依次增加，生成训练集对应的模型（使用线性回归，2次多项式，100次多项式），使用相同的测试集测试对应的模型，并且绘制成x=训练集的个数，y=均方误差来看下欠拟合（线性回归），最佳拟合（二项式），过拟合（20项式）
下面绘制学习曲线的函数封装一下，方便后面调用
def plot_learning_curve(algo, x_train, x_test, y_train, y_test):
train_score = []
test_score = []
for i in range(1, len(x_train)+1):
algo.fit(x_train[:i], y_train[:i])
y_train_predict = algo.predict(x_train[:i])
train_score.append(mean_squared_error(y_train[:i], y_train_predict))
y_test_predict = algo.predict(x_test)
test_score.append(mean_squared_error(y_test, y_test_predict))
plt.plot([i for i in range(1, len(x_train)+1)], np.sqrt(train_score), label='train')
plt.plot([i for i in range(1, len(x_train)+1)], np.sqrt(test_score), label='test')
plt.legend()
plt.axis([0, len(x_train)+1, 0, 4])
plt.show()
plot_learning_curve(LinearRegression(), x_train, x_test, y_train, y_test)
生成数据集
np.random.seed(666)
np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
x_train, x_test, y_train, y_test = train_test_split(X, y, random_state=10)
使用线性回归，图像是欠拟合（欠拟合指模型不能在训练集上获得足够低的误差），训练数据误差都达到2.0了
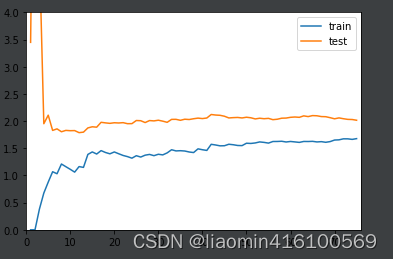
使用二项式回顾，图像是最佳拟合
def PolynomialRegression(degree):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scale', StandardScaler()),
('lin_reg', LinearRegression())
])
poly2_reg = PolynomialRegression(degree=2)
plot_learning_curve(poly2_reg, x_train, x_test, y_train, y_test)
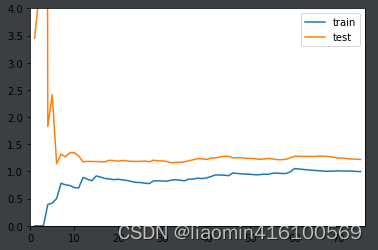
使用20项式，过拟合（过拟合则是指模型在训练集上表现很好，但在测试集上却表现很差）
poly2_reg = PolynomialRegression(degree=20)
plot_learning_curve(poly2_reg, x_train, x_test, y_train, y_test)
