一、MinIO概述
官网地址:http://www.minio.org.cn/
文档地址:http://docs.minio.org.cn/docs/
MinIO是一款基于Apache License v2.0开源协议的分布式文件系统(或者叫对象存储服务),可以做为云存储的解决方案用来保存海量的图片、视频、文档等。由于采用Golang实现,服务端可以工作在Windows、Linux、 OS X和FreeBSD上。配置简单,基本是复制可执行程序,单行命令就可以运行起来。
MinIO兼容亚马逊S3(Simple Storage Service,简单存储服务)云存储服务接口,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等,而一个对象文件可以是任意大小,从几kb到最大5T不等。
MinIO特点:
- 高性能:作为高性能对象存储,在标准硬件条件下它能达到55GB/s的读、35GG/s的写速率;
- 可扩容:不同MinIO集群可以组成联邦,并形成一个全局的命名空间,并跨越多个数据中心;
- SDK支持: 基于Minio轻量的特点,它得到类似Java、Python或Go等语言的sdk支持;
- 支持纠删码:MinIO使用纠删码、Checksum来防止硬件错误和静默数据污染。在最高冗余度配置下,即使丢失1/2的磁盘也能恢复数据;
MinIO基本概念:
- bucket(桶) :类似文件系统的目录(文件夹);
- Object : 类似文件系统的文件;
- Keys :类似文件名;
- MINIO_ACCESS_KEY:访问key,类似账号;
- MINIO_SECRET_KEY:秘钥,类似密码。
文件存储方式对比:
| 存储方式 | 优点 | 缺点 |
|---|---|---|
| 服务器磁盘 | 开发便捷,成本低 | 扩展困难 |
| 分布式文件系统(开源:FastDFS、MinIO) | 容易实现扩展 | 复杂度高 |
| 第三方存储(阿里云OSS、七牛云) | 开发简单,功能强大,免维护 | 收费 |
分布式文件系统对比:
- FastDFS是阿里余庆做的个人项目,也是一款开源高性能的分布式文件系统,适合小规模文件数据存储,默认不提供UI界面,安装部署(运维)复杂,很难达到以G为单位的每秒读写速度,没有完备的官方文档,环境搭建较为复杂;
- MinIO是由MinIO.Inc运营的开源项目,号称世界上速度最快的对象存储服务器,并且社区活跃度高,标准硬件条件下它能达到55GB/s的读、35GB/s的写速率,而且MinIO部署自带管理界面,不需要额外安装;MinIO提供了所有主流开发语言的SDK,并且兼容亚马逊S3云存储服务接口,在MinIO中一个对象文件可以是任意大小,从几KB到最大的5T不等;最后它提供了与k8s、etcd、docker等容器技术深度集成方案,可以说就是为云原生而生的。(缺点,不支持动态增加节点)
- 更详细文章参考:https://www.cnblogs.com/loveer/p/16857625.html
二、MinIO环境搭建
本文基于Docker实现MinIO环境快速部署,Docker安装参考:https://blog.csdn.net/qq_46921028/article/details/129096134
1、拉取镜像(https://hub.docker.com/r/minio/minio/tags)
# 下载新版minio
docker pull minio/minio
# 下载指定版本的minio
docker pull minio/minio:RELEASE.2021-04-06T23-11-00Z
2、创建容器
docker run -p 9000:9000 --name minio -d --restart=always -e "MINIO_ACCESS_KEY=minio" -e "MINIO_SECRET_KEY=minio123" -v /docker/minio/data:/data -v /docker/minio/config:/root/.minio minio/minio server /data
# 或者指定镜像版本并创建容器
docker run -p 9000:9000 --name minio -d --restart=always -e "MINIO_ACCESS_KEY=minio" -e "MINIO_SECRET_KEY=minio123" -v /docker/minio/data:/data -v /docker/minio/config:/root/.minio minio/minio:RELEASE.2021-04-06T23-11-00Z server /data
- -p 9000:9000 ,端口映射
- -e,环境遍历
- -d,后台运行
- –name,给容器起名字
- –restart=always,开机自启
- “MINIO_ACCESS_KEY=minio”,账号
- “MINIO_SECRET_KEY=minio123”,密码
- -v 挂载数据卷

3、测试访问MinIO后台系统,直接浏览器访问 http://ip:9000 即可,账号minio,密码minio123
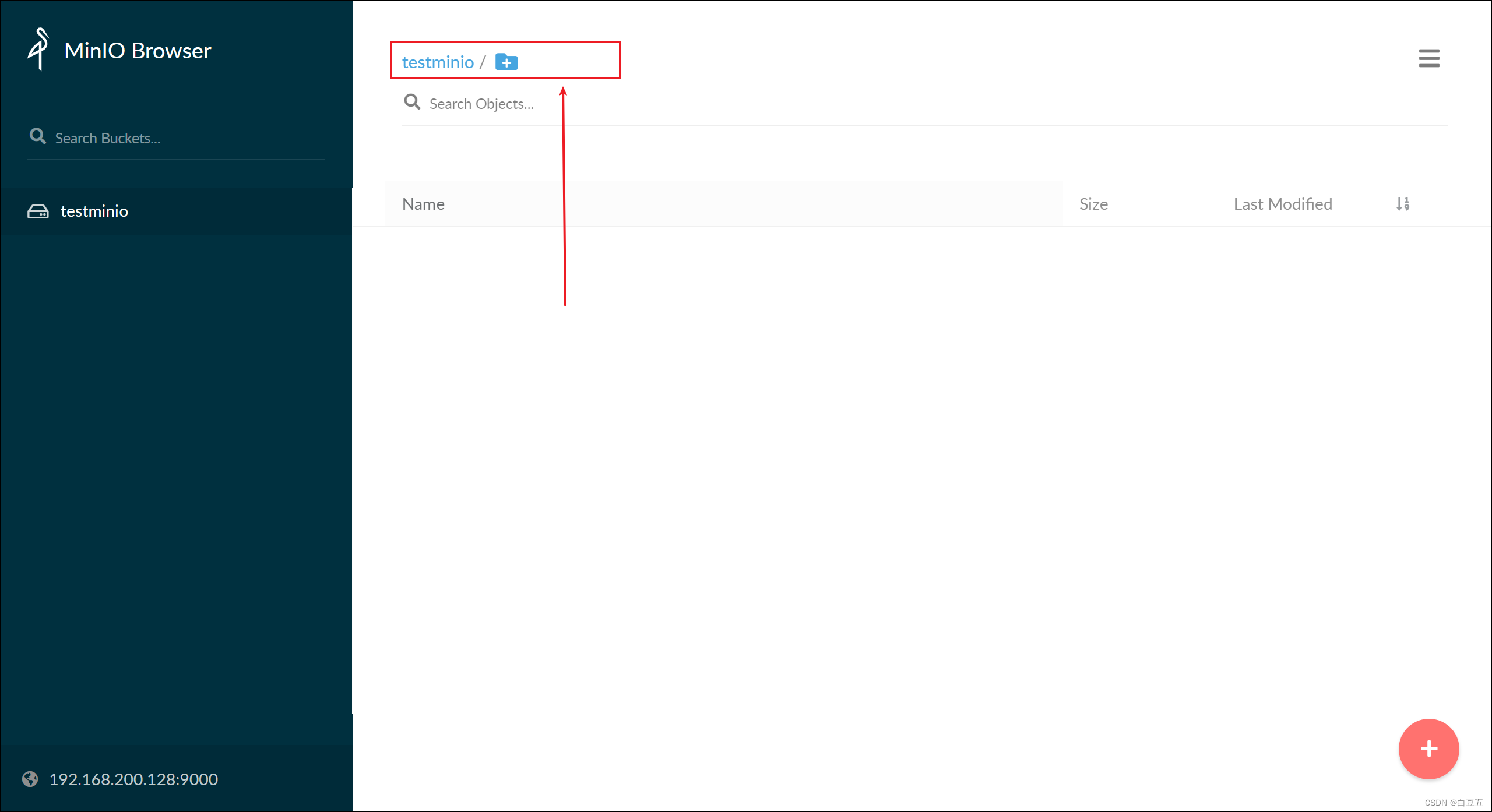
管理界面:
4、创建 bucket(桶)
首先点击右下角的"+"号,创建一个桶
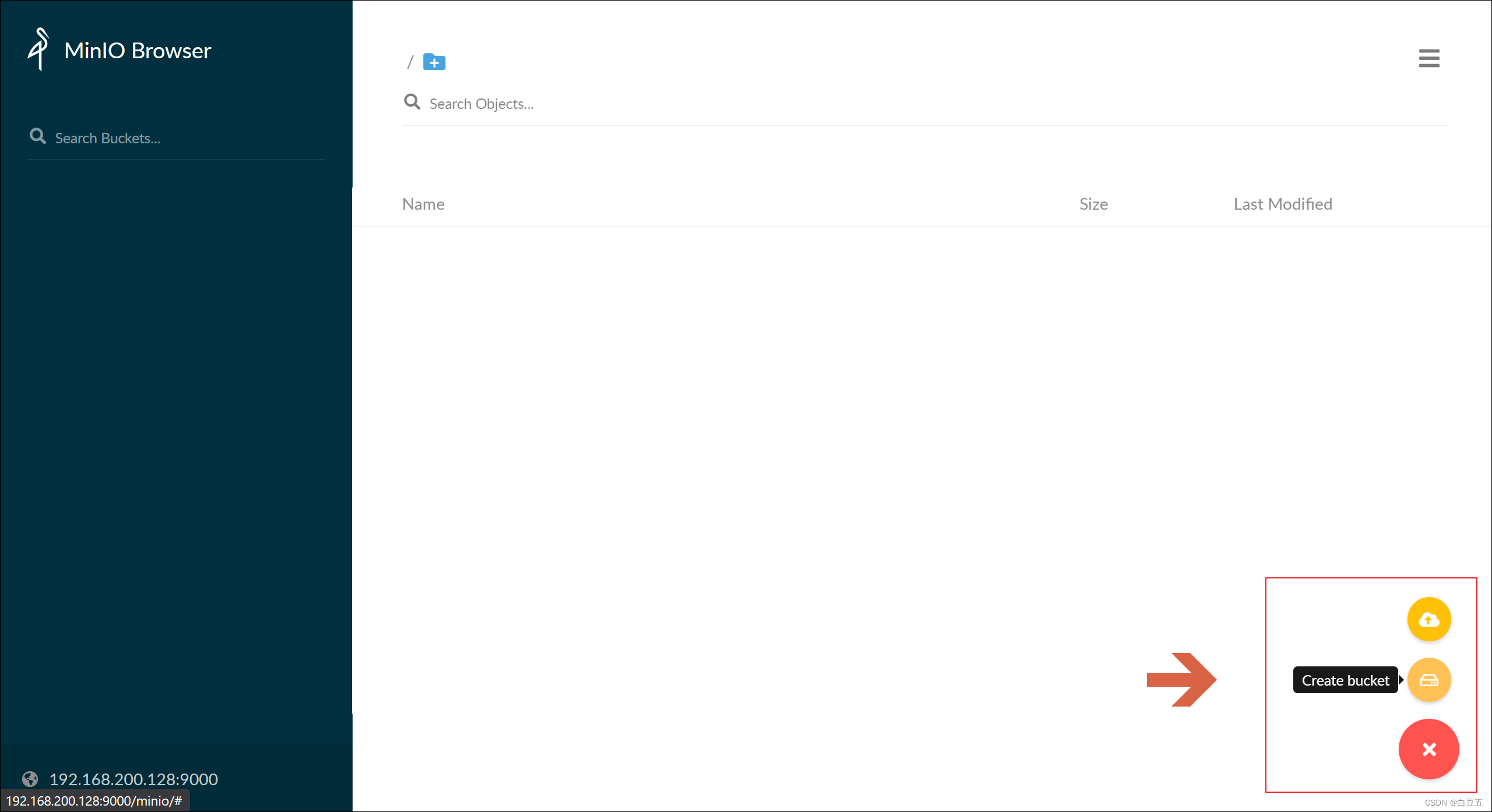
给创建的桶起个名字:
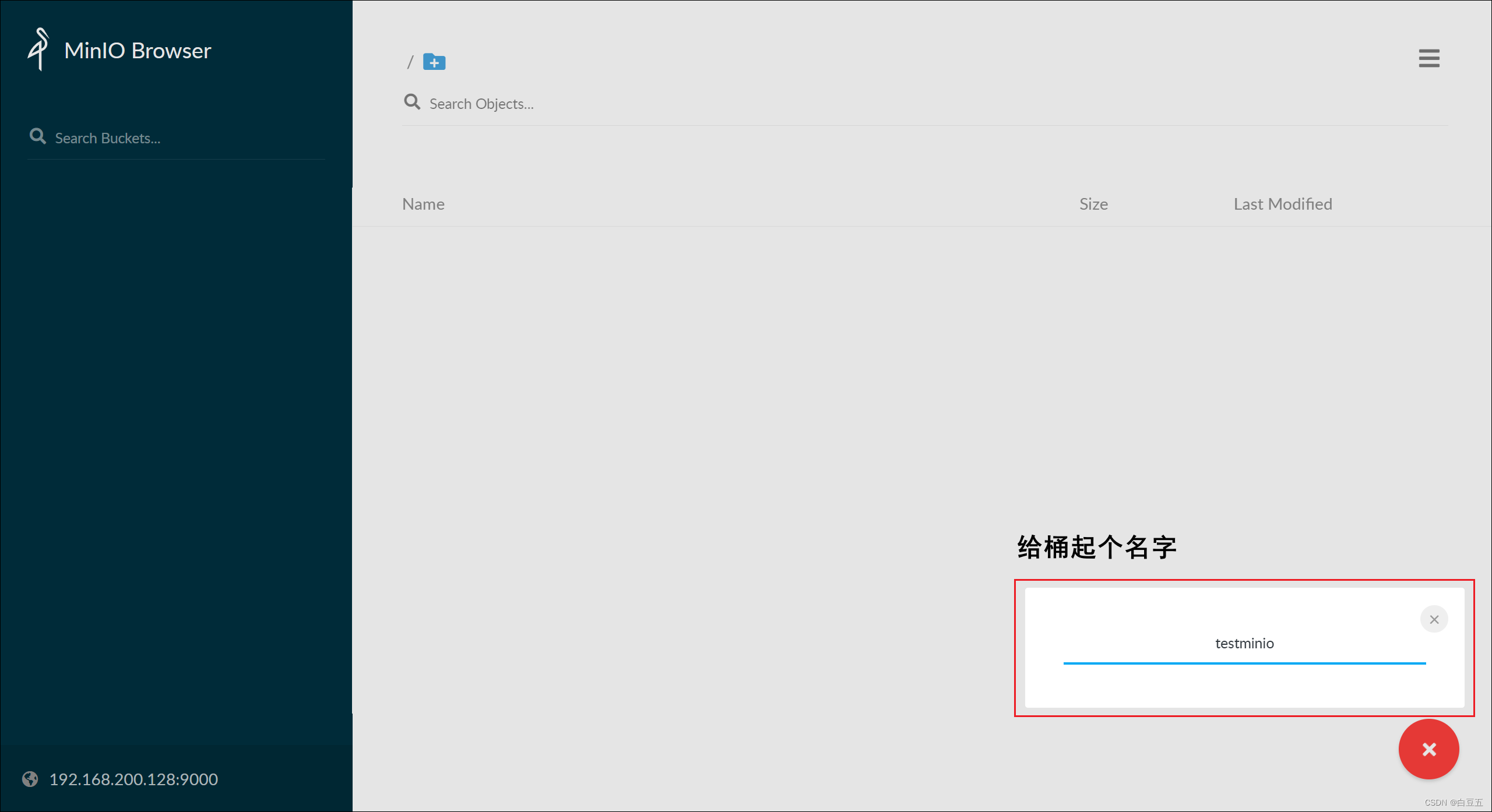
最后在minio管理界面就能看到刚刚创建的桶结构: