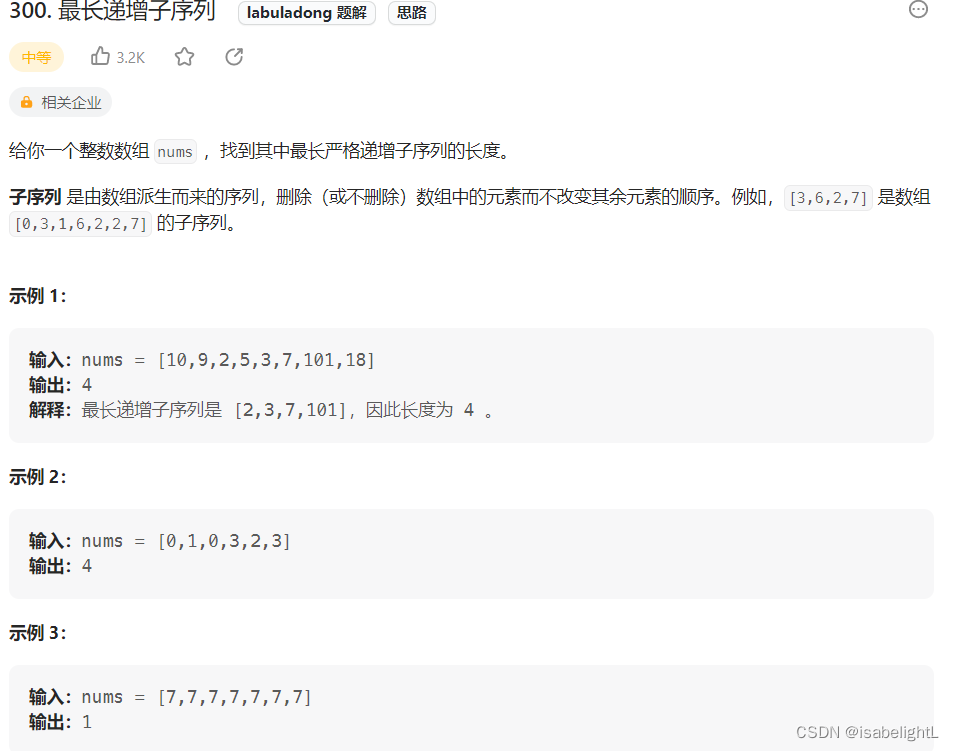
300 最长递增子序列
链接:力扣
看了思路之后写的代码,不知道为什么报错了。
错误一:
int n=nums.size(); vector<int>dp(n,0); dp[0]=1; for(int i=1;i<n;i++) { for(int j=0;j<i;j++) { if(nums[i]>nums[j]) { dp[i]=max(dp[i],dp[j]+1); } } } return dp[n-1];嗷嗷嗷以nums[n-1]为结尾的最长递增子序列未必是整个序列的最长递增子序列。
比如
nums = [10,9,2,5,3,7,101,18]最长递增子序列是 [2,3,7,101],因此长度为 4它的最长递增子序列就不是最后一个元素。所以必须再遍历一遍得到的dp[j],返回最大值。
错误二:
dp数组的初始化值不应该为0,而应该是1.
因为以nums[i]为末尾元素的最长递增子序列至少长度为1.改正之后正确。
class Solution { /* 1、一开始和最长公共子序列搞混,嗷嗷嗷没想法 dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度 2、状态转移方程 位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。 所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1); 怎么理解: 举例:[10,9,2,5,3,7,101,18] 比如现在i指针已经到了i=3,nums[i]=5 dp[i]代表以5为结尾的最长子序列长度 要检查5之前的、以10、9、2为结尾的最大长度,如果5>2,则 需要比较------以2为结尾的最大长度+1,当前dp[3] 这样找到最大的dp[3] */ public: int lengthOfLIS(vector<int>& nums) { int n=nums.size(); vector<int>dp(n,1); //dp[0]=1; for(int i=1;i<n;i++) { for(int j=0;j<i;j++) { if(nums[i]>nums[j]) { dp[i]=max(dp[i],dp[j]+1); } } } int max_len=0; for(int j=0;j<n;j++) { cout<<dp[j]<<" "; max_len=max(max_len,dp[j]); } return max_len; } };
674. 最长连续递增序列
链接:代码随想录
自己的做法,看了一下思路为贪心
class Solution { public: int findLengthOfLCIS(vector<int>& nums) { int n=nums.size(); int max_len=1; int temp_len=1; for(int i=1;i<n;i++) { if(nums[i]>nums[i-1]) { temp_len++; } else { max_len=max(max_len,temp_len); temp_len=1; } } max_len=max(max_len,temp_len); return max_len; } };
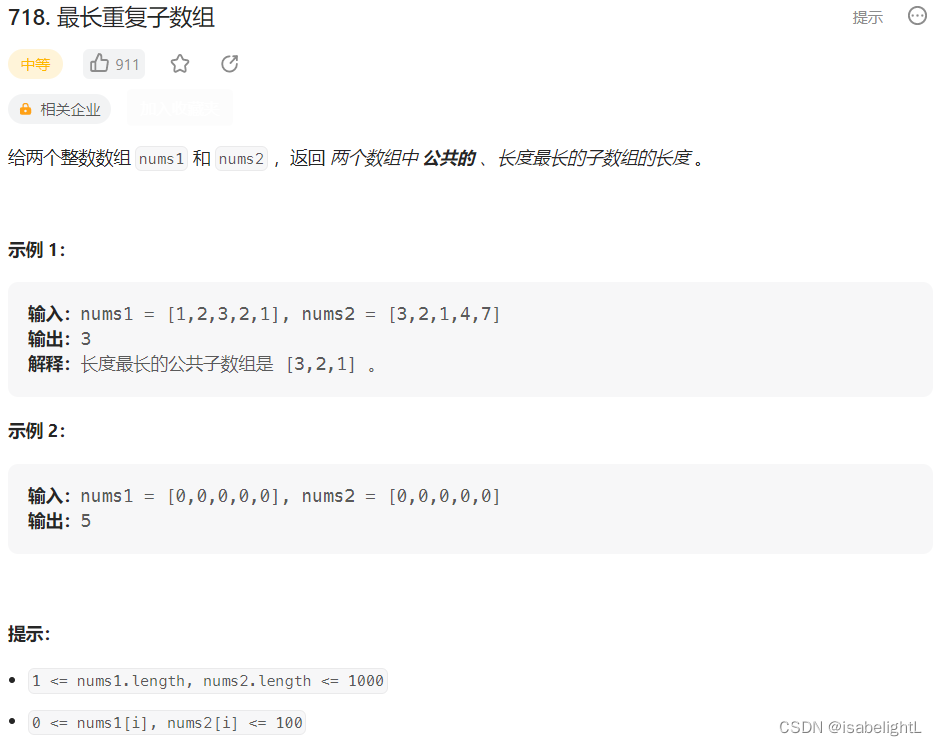
718. 最长重复子数组
链接:代码随想录
思路:

一开始写的代码,但是返回值不对
class Solution { /* 也不是最大公共子序列,要求的是公共的 、长度最长的子数组的长度。 也就是说要连续。 但是整体的思路和最长公共子序列那道题很像 */ public: int findLength(vector<int>& nums1, vector<int>& nums2) { int n1=nums1.size(); int n2=nums2.size(); vector<vector<int>>dp(n1+1,vector<int>(n2+1,0)); for(int i=1;i<n1+1;i++) { for(int j=1;j<n2+1;j++) { if(nums1[i-1]==nums2[j-1]) { dp[i][j]=dp[i-1][j-1]+1; } } } //打印dp二维数组 for(int i=0;i<n1+1;i++) { for(int j=0;j<n2+1;j++) { cout<<dp[i][j]<<" "; } cout<<endl; } return dp[n1][n2]; } };打印的二维数组是对的
思考,按照dp[i][j]是以nums1[i-1]、nums2[j-1]为结尾的最长重复子数组的长度这种定义,不应该返回dp[n1-1][n2-1]这种。而应该和674题一样,遍历寻找最大值。
改正后代码:
class Solution { /* 也不是最大公共子序列,要求的是公共的 、长度最长的子数组的长度。 也就是说要连续。 但是整体的思路和最长公共子序列那道题很像 */ public: int findLength(vector<int>& nums1, vector<int>& nums2) { int n1=nums1.size(); int n2=nums2.size(); vector<vector<int>>dp(n1+1,vector<int>(n2+1,0)); int max_len=0; for(int i=1;i<n1+1;i++) { for(int j=1;j<n2+1;j++) { if(nums1[i-1]==nums2[j-1]) { dp[i][j]=dp[i-1][j-1]+1; } max_len=max(max_len, dp[i][j]); } } //打印dp二维数组 /* for(int i=0;i<n1+1;i++) { for(int j=0;j<n2+1;j++) { cout<<dp[i][j]<<" "; } cout<<endl; }*/ return max_len; } };