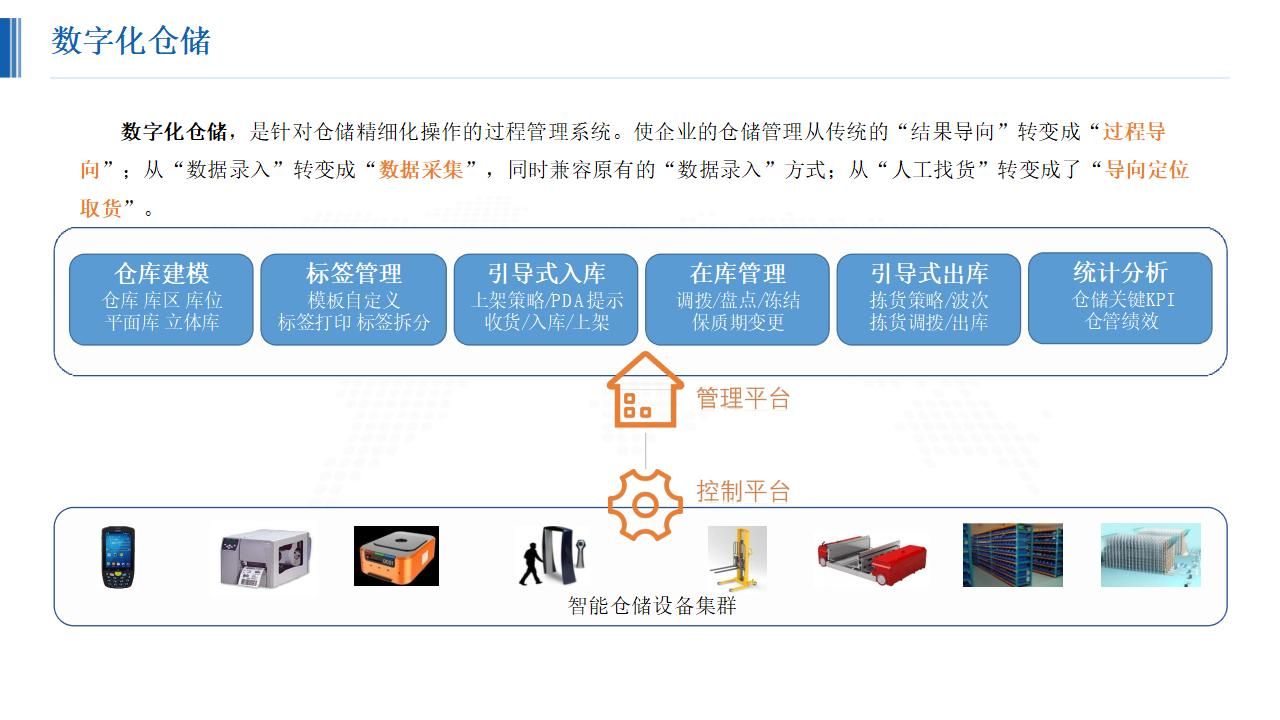
一、概览
现实世界中很多真实的问题都不是线性可分的,即无法使用一条直线、平面或者超平面分割不同的类别,其中典型的例子是异或问题(Exclusive OR,XOR),即假设输入为x1和x2,如果它们相同,即当x1 = 0、x2 = 0或x1 = 1、x2 = 1时,输出y=0;如果它们不相同,即当x1 = 0、x2 = 1或x1 = 1、x2 = 0时,输出y = 1,如下图所示。此时,无法使用线性分类器恰当地将输入划分到正确的类别。

二、定义
多层感知器
(Multi-layer Perceptron,MLP)是解决线性不可分问题的一种解决方案。多层感知器指的是堆叠多层线性分类器,并在中间层(也叫隐含层,Hid-den layer)增加非线性激活函数。例如,可以设计如下的多层感知器:

等式中,ReLU(Rectified Linear Unit)是一种非线性激活函数, 其定义为当某一项输入小于0时,输出为0;否则输出相应的输入值,即
ReLU(z)=max(0, z)。W [i]和b [i]分
别表示第i层感知器的权重和偏置项。
如果将相应的参数进行如下的设置:
 ,b [1] = [0,−1] ⊤ ,W [2] = [1,−2],b [2] = [0]。
,b [1] = [0,−1] ⊤ ,W [2] = [1,−2],b [2] = [0]。
这样即可解决异或问题,该多层感知器的网络结构如下图所示。

那么,该网络是如何解决异或问题的呢?其主要通过两个关键的技术,即增加了一个含两个节点的隐含层(h)以及引入非线性激活函数 (ReLU)。通过设置恰当的参数值,将在原始输入空间中线性不可分的问题映射到新的隐含层空间,使其在该空间内线性可分。
如下图所示,
原空间内
x
=[0,0]和
x
=[1,1]两个点,分别被映射到
h
=[0,0]和
h
=
[2,1];而
x
=[0,1]和
x
=[1,0]两个点,都被映射到了
h
=[1,0]。此时
就可以使用一条直线将两类点分割,即成功转换为线性可分问题。

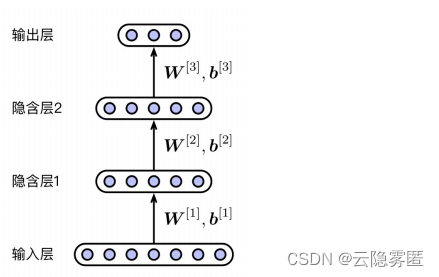
三、更一般的形式
下图展示了更一般的多层感知器,其中引入了更多的隐含层(没有画出非线性激活函数),并将输出层设置为多类分类层(使用 Softmax 函数)。输入层和输出层的大小一般是固定的,与输入数据的 维度以及所处理问题的类别相对应,而隐含层的大小、层数和激活函数的类型等需要根据经验以及实验结果设置,它们又被称为超参数 (Hyper-parameter)。一般来讲,隐含层越大、层数越多,即模型的参数越多、容量越大,多层感知器的表达能力就越强,但是此时较难优化网络的参数。而如果隐含层太小、层数过少,则模型的表达能力会不足。为了在模型容量和学习难度中间寻找到一个平衡点,需要根据不同的问题和数据,通过调参过程寻找合适的超参数组合。