氢原子光谱、类氢原子光谱和类氢离子光谱

news2025/1/9 15:09:37

一、氢原子光谱

（1）万分之五的差值

在文章“原子的波尔模型、能量量子化、光电效应、光谱实验、量子态、角动量”的第3.3节角动量量子化中，通过公式联立获得得里德伯常数要比经验获得的相差万分之五。

当然这时候有人会想是不是实验测得不准确呢，毕竟实验设备存在误差，但当时光谱仪的精度可达万分之一，所以此差值显然并非实验设备精度导致。

为此，玻尔在1914年对此作出了回答。在玻尔原子理论中假定氢核是静止的，电子绕固定不动的核进行运动。事实上，只有当核的质量无限大时才可以有此近似。

而氢核只比电子重约1836倍，这样的近似处理显然会带来误差。实际情况是电子和核绕它们的共同质心运动，如下图：

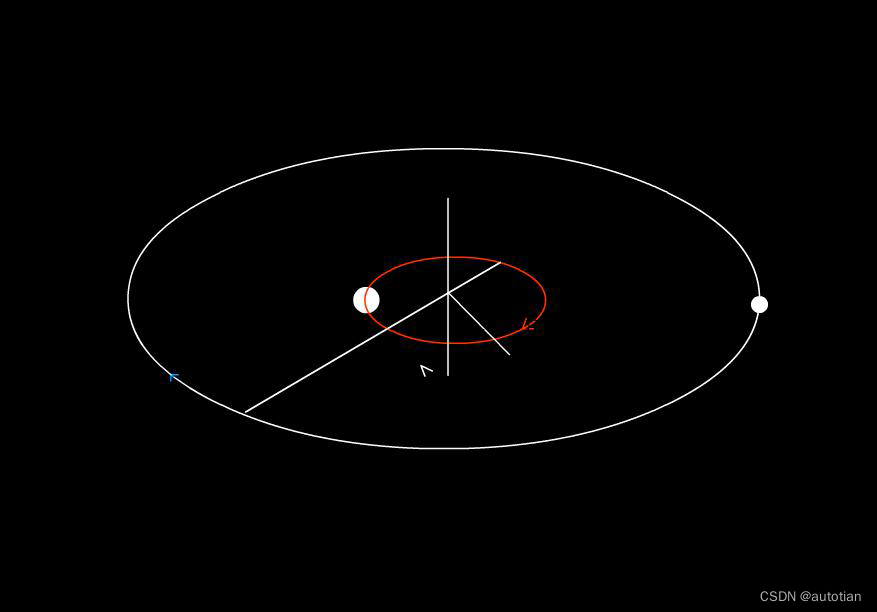
（2）约化质量

对于原子核和电子均绕质心旋转的问题，可利用力学中的两体问题简化为一体问题的方法，即约化质量。

核心思想：当两个物体 $\left(m_1, m_2\right)$ 绕其质心旋转，若想将两体问题转化为一个质点围绕另一个质点运动，这时，可将质量大的 $\left(m_1\right)$ 视为静止，另一个质量小的 $\left(m_2\right)$ 等价为：

$\mu=\frac{m_1 m_2}{m_1+m_2}$

将 $\mu$ 称为约化质量。

之前计算中（文章“原子的波尔模型、能量量子化、光电效应、光谱实验、量子态、角动量”的第3.3节），当原子核质量 $M \rightarrow \infty$ 时， $R_{\mathrm{A}}=\mathrm{R}_{\infty}=109737.31 \mathrm{~cm}^{-1}$ ，修正后的里德伯常数为：

$\begin{aligned} R_H & =R_{\infty} \cdot \frac{M}{M+m_e} \\ & =109737.31 \times \frac{1836}{1837}=109677.57 \end{aligned}$ （M为氢核的质量，me为电子的质量）

而经验常数为： $R=109677.58 \mathrm{~cm}^{-1}$ ，可见相差的非常小。

二、类氢原子光谱

里德伯常数随原子核质量变化的情况也被用于证实氢的同位素——氘的存在。

期初，在原子质量测定问题中，有人估计存在质量为两个单位的重氢。

1932年，尤雷在实验中发现，液氢赖曼系的头四条谱线都是双线，且双线之间波长差的测量值与通过里德伯常数R计算出来的双线波长差非常接近，从而确定了氘的存在。

（1）理论推导波长差

对于氢原子核氘原子，二者的波数分别为：

$\tilde{v}_H=R_H\left(\frac{1}{n^2}-\frac{1}{n^{\prime 2}}\right)$ （氢原子波数）， $\tilde{v}_D=R_D\left(\frac{1}{n^2}-\frac{1}{n^{\prime 2}}\right)$ （氘原子波数）

对于二者的里德伯常数，与本文一中推导类似，均可以表示为质量趋于无穷的里德伯常数乘以它们对应质量部分项，即：

$R_A=R_{\infty} \cdot \frac{M}{M+m_e}=R_{\infty} \cdot \frac{1}{1+\frac{m_e}{M}}$ （其中M为氢原子或氘原子的质量）

对于氢原子和氘原子的同一条谱线，可以得到有如下关系：

$\frac{\Delta \lambda}{\lambda_H}=\frac{\lambda_H-\lambda_D}{\lambda_H}=1-\frac{R_H}{R_D}$

将， $R_A$ 的表达式带入，可以得到： $\frac{R_H}{R_D}=\frac{M_H}{M_H+m} \cdot \frac{M_D+m}{M_D}$ 。

根据氢原子核质量是电子质量的1836倍，且 $M_D=2 M_H$ ，即：

$\frac{R_H}{R_D}=\frac{1836 * 2+1}{2(1836+1)}=0.9997278$

进而可以得到： $\frac{\Delta \lambda}{\lambda_H}=0.000272$

（2）实验波长差

多出的谱线是来自氢原子的同位素氘。
考虑核质量的影响分别计算氢原子和氘原子光谱波长值，并给出了波长差的理论数值

波长差随着波长的增加而减小

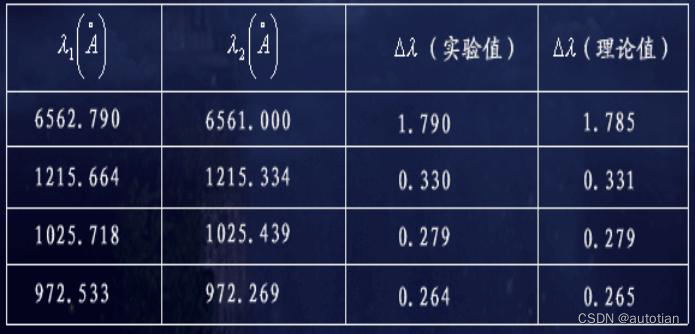
通过对实验波长差和理论推导波长差的对比可见相差很小，可以判定存在质量为2的同位素——氘。

三、类氢离子光谱

类氢离子是指原子核外仅有一个电子的原子体系，但原子核内带有大于一个单位的正电荷。

如一次电离的氦离子 $\mathrm{He}^{+}$ ，二次电离的锂离子 $L i^{++}$ ，三次电离的铍离子 $B e^{+++}$ ，都是具有类似氢原子结构的离子。

（1）毕克林系的发现

1897年，天文学家毕克林在船舻座ζ星的光谱中发现了一个很像巴耳末系的线系。如下图：

其中高的谱线为巴尔末系，和巴尔末系谱线挨的比较近且较矮的谱线为毕克林系。

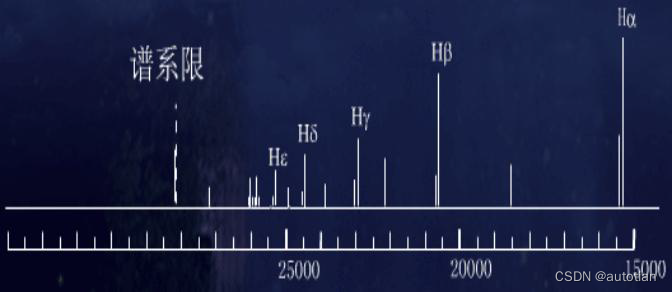
通过谱线的观察，可以得到以下判断：

毕克林系中每隔一条谱线和巴尔末系的谱线差不多重合，但另外有一些谱线位于巴尔末系两邻近线之间；
毕克林系和巴耳末系差不多相重合的哪些谱线，波长稍有差别。（起初有人成为毕克林系为外星上氢的光谱线）

（2）类氢离子里德堡常数

在“原子的波尔模型、能量量子化、光电效应、光谱实验、量子态、角动量”一文中我们知道，里德堡常数的表达式为： $R_H=\frac{2 \pi^2 Z^2 e^4 m_e}{\left(4 \pi \varepsilon_0\right)^2 \cdot c h^3}$ ，并根据其推导过程，可以知道，当质量变为Z时， $e^2$ 需要补一个Z，则 $e^4$ 需要补 $Z^2$ 。进而得到类氢离子的德堡常数表达式为：

$\mathrm{R}_A=\frac{2 \pi^2\left(Z e^2\right)^2 \mu}{\left(4 \pi \varepsilon_0\right)^2 h^3 c}=\frac{2 \pi^2 e^4 \mu}{\left(4 \pi \varepsilon_0\right)^2 h^3 c} Z^2$