0 背景
在营销等场景下,有种常见的玩法,即抽奖,不论前端抽奖界面如何炫酷,底层抽奖组件具有一致性。本文不讨论奖池的抽取规则、奖池奖品配置、奖池切换、抽奖机会、奖品扣减和发放、告警和降级等,主要聚焦于抽奖算法。
1 抽奖算法
对于 1.1 和 1.2 中的算法这里作如下约定:
- 待抽取的奖品有1 部 iphone(10%),3 部 ipad(30%),6 副 airpods(60%)
1.1 暴力算法
最容易想到的就是,所有的物品都放在一个箱子里,然后抽取。以当前的物品为例,按照某种顺序(个数)排列如下:

生成一个 [0, 10) 的随机数,落在哪里就取出对应的奖品,预处理空间复杂度 O(奖品总个数),预处理时间复杂度 O(奖品总个数),生成随机数(角标)取出对应奖品的时间复杂度 O(1)。算法时间复杂度 O(奖品总个数),空间复杂度 O(奖品总个数)。
1.2 离散算法
参看暴力算法的图解,很容易发现相同颜色的代表同一个物品,每一个格子都是一样的内容,那我们考虑消除这些冗余的格子,如果仅仅留下红蓝绿三个格子,那么如果直接随机,我们发现无法保重对应物品的概率。因此我们需要给物品一定的权重,权重就是物品的概率,处理后的数组如下:

现在预处理数组长度就是奖品种类,预处理的数组中的值是前缀和 sum of [0, count(i)) ,现在的规则还是生成一个 [0, 10) 的随机数,记做 R,但是角标无法直接找到对应的奖品。因此需要遍历数组进行比较,找到第一个数组值大于改 R 的位置的奖品即可,为了加快查询速度,可以使用二分查找(upper_bound)。算法时间复杂度 O(奖品种类),空间复杂度 O(奖品种类)。
有没有更快的算法,答案是有!
1.3 The Alias Method
中文名字叫做别名方法或别名采样算法,是一种时间复杂度为 O(1) 的离散采样算法,可以用于抽奖算法。
这里根据上述论文按照图文的方式简单介绍一下,并做简要的论证,详细论证自行参见论文。
这里也是按照论文的例子进行叙述,避免重复作图。
1.3.1 算法的思路起源:
1、让我们产生一组如下概率分布的离散采样:
1
2
、
1
3
、
1
12
、
1
12
\frac {1} {2}、\frac {1} {3}、\frac {1} {12}、\frac {1} {12}
21、31、121、121
然后我们作如下柱状图,概率为其高度,概率和为1,如果我们记宽度为 w,那面积就是 1 w。
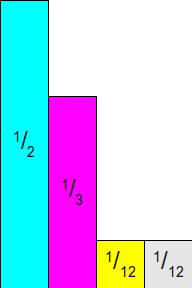
2、现在我们把上图的其余部分填充,使得其成为一个矩形,如图所示:

3、我们把左边的最大的概率变成1,所有概率乘以2,如图所示

4、补充每一个列的上方,每一个列都是一个概率为1的事件,我们做两次操作,第一次掷数字范围在 [1, 4] 的骰子决定我去哪一个列,第二次我们产生 0~1 之间的随机数,如果落在有概率的范围内,我们就返回这个事件,但是要注意,如果我们落在概率范围之外,那么我们需要重新采样。比如我们第一次数字是 2,那么我们将有 1/3 的概率失败,需要重新采样,最好情况的时间复杂度是 O(1),最差情况的话时间复杂度是无穷。那平均复杂度是多少呢,可以看到命中的面积时 2w,没有命中的面试是 2w,可以认为命中概率 1 - (1 / 2)^x 中 x = n(物品数)就是一个接近 1 的数字,可以认为平均时间复杂度是 O(n)

说到这里,我们需要处理连续采样没有命中的情况!这样我们才有可能在 O(1) 时间复杂的范围完成采样。
在上文中,我们有一个东西没有用到,但是我们还给它画了出来,那就是没有命中的那一块区域的面积!
那有没有可能我们把没有命中的地方面积(红色)使用其他命中的面积(非红色)中移过来一点进行填充,那这样岂不是必定会命中某一个事件。
接下来,就是正菜 The Alias Method!
1.3.2 The Alias Method
还是上述柱状图,不过我们使得矩形的宽度 w = 1,得到下图:

我们对上图的矩形进行伸缩,伸缩尺度为 n = 4(事件个数),得到下图
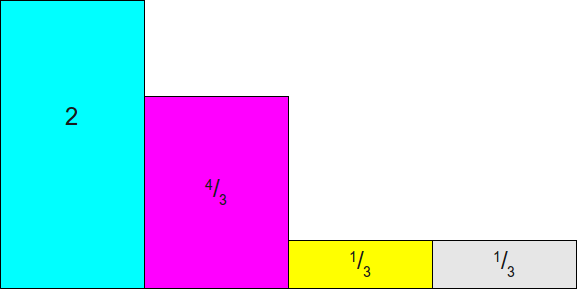
我们再次作一个 1 * 4 的矩形,如下图:
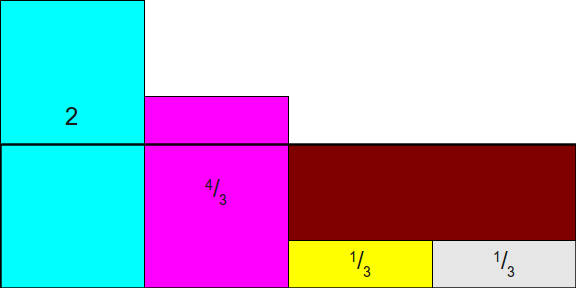
正如你所看,我们考虑将多出的矩形面积用来填充到红色区域,我们将绿色拿出一部分放在灰色上面,如下图所示:
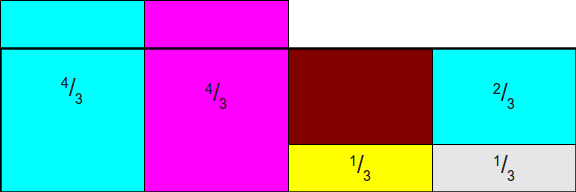
那现在有个问题,我们能直接把绿色和粉色的对于面积放在黄色上面吗,如果放在上面,我们第三列将会有三个事件,最糟糕情况第三列将会有 N 个事件,N 个事件的概率问题又回到最初的原点,因此我们需要保证每一列不超过两种事件,这样就是一种非 a 即 b 选择,这也是 The Alias Method 需要保证的。所以我们可以使用绿色面积填充到黄色上面。
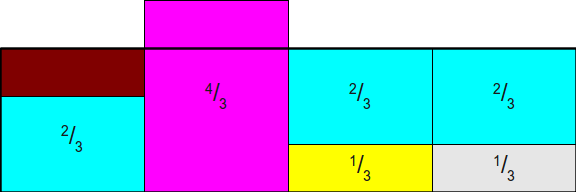
然后多余粉色部分填充到绿色上方,这样我们的到一个面积全是 1 且每一列只有两种事件的最终矩形!

这里采样算法采样过程还是两次,具体不在讲解,很好理解。
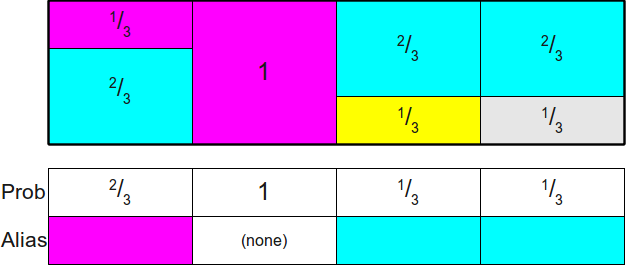
可以看出,The Alias Method 关键在于如何构建 Prob 和 Alias 数组。
构建方法:找出大于 1 的事件(A)和小于 1 的事件(B),然后让其事件 A 将事件 B 的面积补到 1,然后事件 A 面积减去被使用的面积判断事件 A 是否需要补充(< 1),如果不需要,那可以继续作为其他事件的面积的补充,知道所有的事件(列)面积都为 1,构建时间复杂度O(n^2)。
我们可以考虑使用优先队列进行加速,使得时间复杂度降为 O(nlogn)。
存在性证明
那么Alias Table一定存在吗,如何去证明呢?
要证明Alias Table一定存在,就说明上述的算法是能够一直运行下去,直到所有列的面积都为1了为止,而不是会中间卡住。
上述方法每运行一轮,就会使得剩下的没有匹配的总面积减去1,在第n轮,剩下的面积为N-n,如果存在有小于1的面积,则一定存在大于1的面积,则一定可以用大于1的面积那部分把小于1部分给填充到1,这样就进入到了第n+1轮,最后一直到所有列面积都为1。
2 代码实现
2.1 The Alias Method
Alias.h
//
// Created by liyang on 2022/9/4.
//
#ifndef DEMO_ALIAS_H
#define DEMO_ALIAS_H
#include <vector>
#include <queue>
class Alias {
public:
class Node {
public:
int pos;
double val;
Node() {}
Node(int i, double p) {
this->pos = i;
this->val = p;
}
bool operator<(const Node &node) const {
return this->val < node.val;
}
bool operator>(const Node &node) const {
return this->val > node.val;
}
};
private:
const double ONE = 1;
int N;
bool generated = false;
std::vector<double> initialProbList;
std::vector<double> probList;
std::vector<int> aliasList;
std::priority_queue<Node, std::vector<Node>, std::less<Node>> maxQue; // 大顶堆
std::priority_queue<Node, std::vector<Node>, std::greater<Node> > minQue; // 小顶堆
public:
Alias(std::vector<double> p);
void generateAliasTable();
int sampling();
bool myEqual(double a, double b);
void myPush(Node& node);
long getTimeNs();
};
#endif //DEMO_ALIAS_H
Alias.cpp
//
// Created by liyang on 2022/9/4.
//
#include "Alias.h"
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;
void Alias::generateAliasTable() {
for (int i = 0; i < N; ++i) {
probList.push_back(Alias::initialProbList[i] * N);
myPush(*new Node(i, probList[i]));
}
Node bigNode, smallNode;
while (!maxQue.empty() && !minQue.empty()) {
bigNode = maxQue.top();
maxQue.pop();
smallNode = minQue.top();
minQue.pop();
double diff = ONE - smallNode.val;
probList[bigNode.pos] -= diff;
bigNode.val -= diff;
aliasList[smallNode.pos] = bigNode.pos;
myPush(bigNode);
}
generated = true;
}
int Alias::sampling() {
if (!generated) {
generateAliasTable();
}
int i = (int) rand() % N;
double r = ((double) rand() / (RAND_MAX)); // double [0, 1)
if (r < probList[i]) {
return i;
}
return aliasList[i];
}
bool Alias::myEqual(double a, double b) {
double smallDiff = 0.000001;
return a >= b ? a - b <= smallDiff : b - a <= smallDiff;
}
Alias::Alias(std::vector<double> p) {
this->initialProbList = p;
this->N = initialProbList.size();
this->aliasList = vector<int>(N, -1);
// set rand seed
srand(getTimeNs());
}
void Alias::myPush(Node &node) {
if (myEqual(node.val, ONE)) {
return;
}
if (probList[node.pos] > ONE) {
maxQue.push(node);
} else if (probList[node.pos] < ONE) {
minQue.push(node);
}
}
long Alias::getTimeNs() {
struct timespec ts;
clock_gettime(CLOCK_REALTIME, &ts);
return ts.tv_sec * 1000000000 + ts.tv_nsec;
}
测试下 The Alias Method 算法
main.cpp
#include <iostream>
#include "Alias.h"
#include <unordered_map>
using namespace std;
int main() {
vector<string> prizeList{"airpods", "ipad", "iphone", "mac"};
vector<double> probList{1.0 / 2.0, 1.0 / 3.0, 1.0 / 12.0, 1.0 / 12.0};
unordered_map<string, string> nameProbMap;
nameProbMap["airpods"] = "0.50";
nameProbMap["ipad"] = "0.33333";
nameProbMap["iphone"] = "0.08333";
nameProbMap["mac"] = "0.08333";
Alias *aliasObj = new Alias(probList);
int pos;
const int testCnt = 1000000;
unordered_map<string, int> um;
for (int i = 0; i < testCnt; ++i) {
pos = aliasObj->sampling();
um[prizeList[pos]]++;
}
cout << "总抽奖次数:" << testCnt << endl;
for (auto e: um) {
cout << "奖品名字:" << e.first << ",抽中次数:" << e.second;
cout << ",抽中概率:" << e.second * 1.0 / (testCnt * 1.0);
cout << ", 理论抽奖概率:" << nameProbMap[e.first] << endl;
}
return 0;
}
结果:
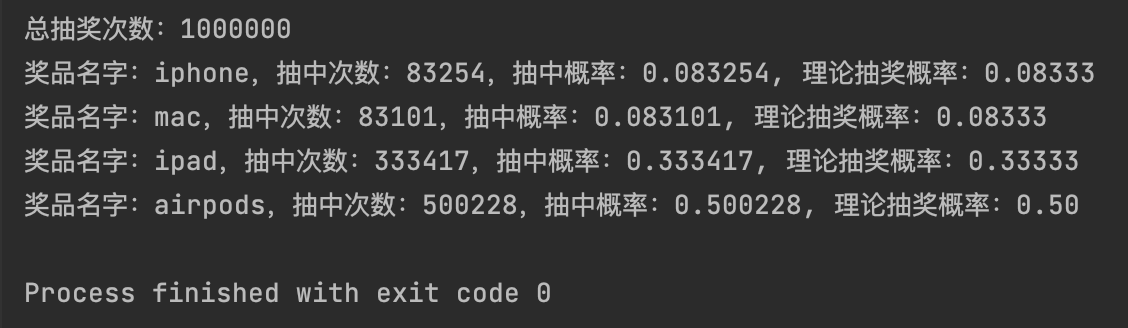
2.2 Vose’s Alias Method
那有没有更快的 Initialization Time,事实上,我们并不需要每次找到最小的和最大的,我们只要找到一个大于1,一个小于1的即可,所以我们维护两个 worklist,存放大于1的称作 large worklist,存放小与1的称为 small worklist,然后不断使用 large 去填补 small 即可,这里我们存角标,具体见下图:

论文中使用栈实现,因为给予栈可以方便的使用数组实现,但我这里直接使用队列实现,因为我有 STL,开箱即用!
代码如下:
Alias.h
/**
* Vose's Alias Method
* liyang 20230414
*/
private:
std::queue<int> small;
std::queue<int> large;
public:
void generateVoseAliasTable();
void myVosePush(int index);
int voseSampling();
void Alias::myVosePush(int index) {
if (myEqual(probList[index], ONE)) {
return; // todo:直接 set one
}
if (probList[index] > ONE) {
large.push(index);
} else { // if (probList[index] < ONE)
small.push(index);
}
}
Alias.cpp
void Alias::myVosePush(int index) {
if (myEqual(probList[index], ONE)) {
return; // todo:直接 set one
}
if (probList[index] > ONE) {
large.push(index);
} else { // if (probList[index] < ONE)
small.push(index);
}
}
void Alias::generateVoseAliasTable() {
for (int i = 0; i < N; ++i) {
probList.push_back(Alias::initialProbList[i] * N);
myVosePush(i);
}
int l, g;
while (!small.empty() && !large.empty()) {
l = small.front();
small.pop();
g = large.front();
large.pop();
aliasList[l] = g;
probList[g] -= (ONE - probList[l]);
myVosePush(g);
}
generated = true;
}
int Alias::voseSampling() {
if (!generated) {
generateVoseAliasTable();
}
int i = (int) rand() % N;
double r = ((double) rand() / (RAND_MAX)); // double [0, 1)
if (r < probList[i]) {
return i;
}
return aliasList[i];
}
可以看到我并没有实现红色圈中的步骤,因为我通过myVosePush调用myEqual的时候就考虑了浮点数的精度问题,因此这一步在这就没有必要了。
bool Alias::myEqual(double a, double b) {
double smallDiff = 0.000001;
return a >= b ? a - b <= smallDiff : b - a <= smallDiff;
}
将调用改成 pos = aliasObj->voseSampling();,测试下结果:
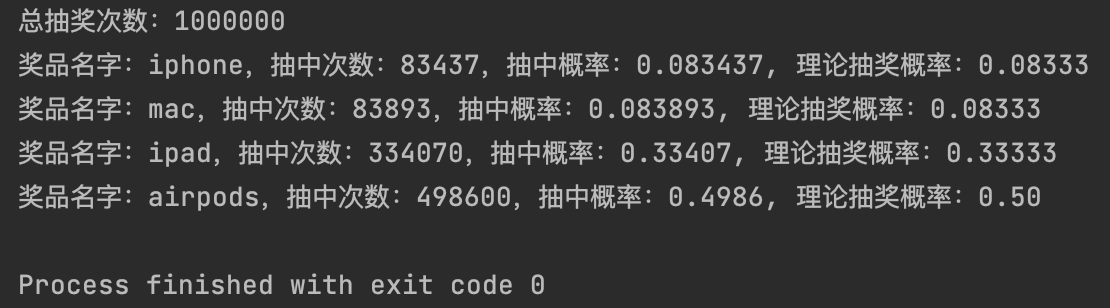
3 总结
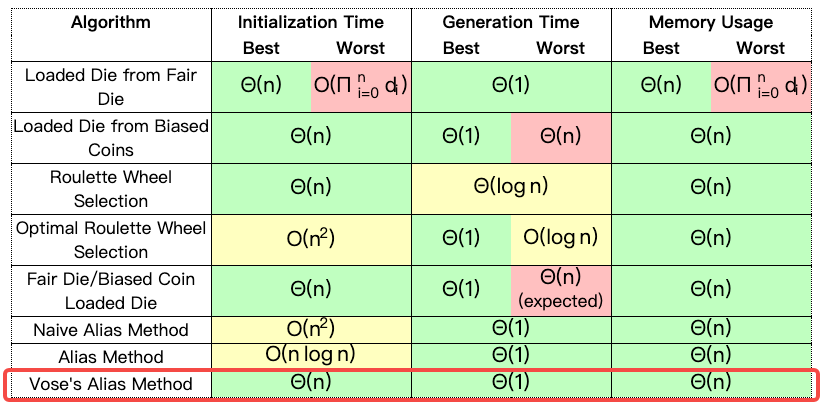
使用 Vose‘s Alias Method,我们可以实现初始化为 O(n) 的算法,采样 O(1) 时间复杂度,空间负责度 O(n)。
如果抽奖的奖品不考虑库存,那么可以抽奖算法就是 O(1) 事件复杂度。每次考虑库存,抽奖物品的种类变动,直接动态生成即可。

![[数据结构 - C语言] 顺序表](https://img-blog.csdnimg.cn/img_convert/f766197ad4bb9bbd8492a153dbd020b4.png)
![逆向-还原代码之(*point)[4]和char *point[4] (Interl 32)](https://img-blog.csdnimg.cn/1cf95bbf676e4a998c6e3da488a72f17.png)