【PyTorch】课堂测试一：线性回归的求解

news2024/9/21 16:27:49

作者🕵️‍♂️：让机器理解语言か

专栏🎇：PyTorch

描述🎨：PyTorch 是一个基于 Torch 的 Python 开源机器学习库。

寄语💓：🐾没有白走的路，每一步都算数！🐾

介绍💬

这个是我们的第一次课堂测试，共有四个挑战，本测试需要你利用前面所学到的 PyTorch 知识，完成线性回归问题的求解，时间为30min。（文末附有参考答案，请大家认真作答再自行校对！）

知识点📜

损失的定义
优化器的定义
模型的训练

线性回归的求解

首先，让我们来模拟一下，线性回归所需的数据集合：

import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
%matplotlib inline

X_numpy, y_numpy = datasets.make_regression(
    n_samples=100, n_features=1, noise=20, random_state=4)
plt.plot(X_numpy, y_numpy, 'ro')

如上，我们初始化了一个数据集合。从图中可以看出，该数据集合大致上呈线性分布。

本挑战的目的就寻找一个良好的函数表达式（又叫做模型），该函数表达式能够很好的描述上面数据点的分布，即对上面数据点进行拟合。

在使用 PyTorch 求解模型之前，我们需要将上面的数据集转为 PyTorch 认识的张量。

🚩挑战①：将 X_numpy，y_numpy 转为张量。

📝要求：转换后的张量用 X,y 表示。

🔔提示：需要利用 tensor.view() 将 y 的维度转为 2 维。

import torch
import torch.nn as nn

# 编写代码处


# 测试代码
X.size(), y.size()

重要说明

本课程中，你需要自行补充上方单元格中缺失的代码并运行，如果输出结果和下方的期望输出结果一致，即代表此挑战顺利通过。完成全部内容后，点击「提交检测」即可通过，此说明后续不再出现。

✅ 期望输出

(torch.Size([100, 1]), torch.Size([100, 1]))

根据上面图像中数据点的分布情况，我们可以看出，该问题的解决模型应该是一个线性函数模型。接下来让我们使用 PyTorch 来初始化这个线性模型。

🚩 挑战②：线性函数模型的定义。

📝 要求：用 model 变量表示线性函数模型。

### 补充代码 ###


# 测试代码
model

✅期望输出

Linear(in_features=1, out_features=1, bias=True)

定义完模型后，接下来，让我们来定义学习率、损失函数和优化器。

🚩 挑战③：利用 PyTorch 定义学习率、损失函数和优化器。

📝 要求：损失采用均方差损失，学习率取 0.01 。

### 补充代码 ###


# 测试代码
optimizer

✅期望输出

SGD (
Parameter Group 0
    dampening: 0
    lr: 0.01
    momentum: 0
    nesterov: False
    weight_decay: 0
)

最后让我们进行模型的训练，即将数据传入模型中，然后利用梯度下降算法不断的迭代，找到最佳的模型。

🚩 挑战④：利用 PyTorch 训练线性模型。

📝 提示：可以循环迭代 100 次左右。

### 补充代码 ###


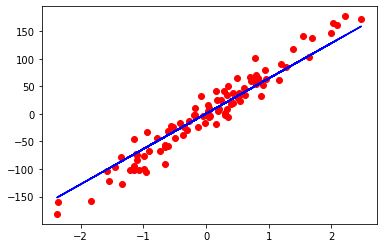
# 测试代码：将通过模型预测出来的值展示到图像中
# 预测结果并转为 NumPy 的形式
predicted = model(X).detach().numpy()

plt.plot(X_numpy, y_numpy, 'ro')
plt.plot(X_numpy, predicted, 'b')
plt.show()

参考答案

本挑战的参考答案如下：

挑战 1 的参考答案

X = torch.from_numpy(X_numpy.astype(np.float32))
y = torch.from_numpy(y_numpy.astype(np.float32))
y = y.view(y.shape[0], 1)

挑战 2 的参考答案

n_samples, n_features = X.shape
input_size = n_features
output_size = 1
model = nn.Linear(input_size, output_size)

挑战 3 的参考答案

learning_rate = 0.01
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

挑战 4 的参考答案

num_epochs = 100
for epoch in range(num_epochs):
    # Forward pass and loss
    y_predicted = model(X)
    loss = criterion(y_predicted, y) 
    # Backward pass and update
    loss.backward()
    optimizer.step()
    # zero grad before new step
    optimizer.zero_grad()
    if (epoch+1) % 10 == 0:
        print(f'epoch: {epoch+1}, loss = {loss.item():.4f}')