一、动态规划（DP）介绍

1、从斐波那契数列看动态规划

（1）问题

斐波那契数列递推式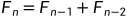： $\text{[math]}$

练习：使用递归和非递归的方法来求解斐波那契数列的第n项

（2）递归方法的代码实现

import time
# 递归求解斐波那契数列
def fibnacci(n):
    if n == 1 or n == 2:
        return 1
    else: # n > 2
        res = fibnacci(n-1) + fibnacci(n-2) # 递推式
        return res

t1 = time.time()   # 开始时间
print(fibnacci(40)) # 运行程序
t2 = time.time() # 结束时间
print(f"递归运行时间：{t2-t1}") # 运行时间

输出结果：

102334155
递归运行时间：30.308536052703857

（3）非递归方法代码实现

import time
# 非递归求解斐波那契数列
def fibnacci_no_rec(n):
    res = [0, 1, 1] # 结果列表，n=0，n=1，n=2时，结果已知
    if n > 2: 
        # 循环递推式，计算结果
        for i in range(n-2): # 例如n=3时，只需要循环一次
            num = res[-1] + res[-2] # 列表的最后一位和列表最后第二位，对应保存的n-1和n-2的值
            res.append(num) # 结果加入到列表中
    return res[n] # 列表第n项，不是res[-1],res有原始3个元素，n<=2时，res[-1]一直是1

t1 = time.time() # 开始时间
print(fibnacci_no_rec(40)) # 运行程序
t2 = time.time() # 结束时间
print(f"非递归运行时间：{t2-t1}")

输出结果：

102334155
非递归运行时间：0.0

（4）动态规划简单理解

1）对比递归方法和非递归方法的运行时间，可以发现同样规模下，斐波那契数列用递归方法计算，运行时间大大超过非递归方法。其主要原因是，递归方法运行是存在子问题的重复运算。即，当计算f(5)时，f(3)将会重复计算2次，f(5)=f(4)+ f(3);f(4)=f(3)+f(2)。

2）非递归方法计算时，每个子问题只计算一次，存在列表中。非递归方法求解斐波那契数列体现了动态规划的思想。

3）动态规划（DP）的思想包含有：

最优子结构，即递推式，只要求解每个子问题的最优解；

重复子问题，必须需要重复计算时，用循环的方式将重复子问题用列表存储起来。

二、钢条切割问题

1、提出问题

某公司出售钢条,出售价格与钢条长度之间的关系如下表:

问题:现有一段长度为n的钢条和上面的价格表，求切割钢条方案，使得总收益最大。

2、问题分析

（1）钢条切割方案举例

长度为4的钢条的所有切割方案如下:(c方案最优)

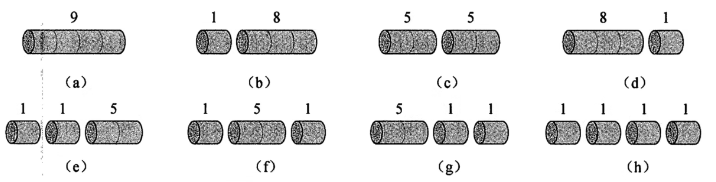
思考: 长度为n的钢条的不同切割方案有几种?

从例子可以看出，长度为4的钢条一共有8种切割方式。因为长度为4的钢条可以切割3处，每处都有切和不切两种选择，根据排列组合原理得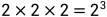： $\text{[math]}$ 。则长度为n的钢条的不同切割方案为 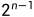$\text{[math]}$ 种。

因此组合方式很多，枚举法求解不合理。

（2）问题求解思路

如上图所示，其中i表示钢条总长度，pi表示整根出售的价格，r[i]表示整个钢条切割后可出售的最高价格，即当前最优解。

1）以i=4时为例，最优解的求解为：

不切割，总价值为9；

切割为1和3，总价值为1+8=9；

切成2和2，总价值为5+5=10，得到最优解。

2）以i=8时为例，最优解的求解为：

不切割，总价值为20；

切成1和7，总价值为19；

切成2和6，总价值为22；

切成3和5，总价值为21；

切成两个4，总价值为20；

对比后，最优解为切成2和6，长度为2的最优解为5，长度为6的最优解为17，其中长度1-7的最优解是如何切割的在假设已经求出，已存储在列表中，因此只需要考虑长度为8时怎么分割价格最高，再回推到长度2和长度6怎么切割价格最高，这就是动态规划的思想，不断求解当前子问题中的最优解。

（3）钢条切割问题-递推式

设长度为n的钢条切割后最优收益值为 $\text{[math]}$ ，可以得出递推式：

$\text{[math]}$

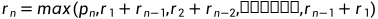
参数说明：

第一个参数 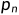$\text{[math]}$ 表示不切割；

其他n-1个参数分别表示另外n-1种不同切割方案，对方案i=1,2,..,n-1：

将钢条切割为长度为i和n-i两段；

方案i的收益为切割两段的最优收益之和。

考虑所有方案，选择其中收益最大的方案。

（4）最优子结构-钢条切割问题

1）可以将求解规模为n的原问题，划分为规模更小的子问题: 完成一次切割后，可以将产生的两段钢条看成两个独立的钢条切个问题。

2）组合两个子问题的最优解，并在所有可能的两段切割方案中选取组合收益最大的，构成原问题的最优解。

3）钢条切割满足最优子结构:问题的最优解由相关子问题的最优解组合而成，这些子问题可以独立求解。

（5）最优子结构的简化

钢条切割问题还存在更简单的递归求解方法：

从钢条的左边切割下长度为i的一段，只对右边剩下的一段继续进行切割，左边的不再切割

递推式简化为 $\text{[math]}$ .

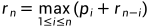不做切割的方案就可以描述为: 左边一段长度为n，收益为Pn，剩余一段长度为0，收益为ro=0。

上述解析：

1）简化后的递推式的计算方式为：

当i=5时，左边不可再切割，右边可继续切割：

切割为1和4，其中1不可再分割，因此总价值为p1+r[4]=1+10=11;

切割为2和3，其中2不可再切割，总价值为p2+r[3]=5+8 =13;

切割为3和2，其中3不可再切割，总价值为p3+r[2]=8+5 =13;

切割为4和1，其中1不可再切割，总价值为p4 + r[1]=9+1=10;

2）原递推式存在的问题：

原递推式也是可以使用的，只不过存在重复计算的情况。

假如，长度为9的钢条，最优切割为（2,2,2,3）,那么根据递推式，可以是4和5,5和4,2和7,7和2，在左右都可分割的情况下，得到的结果都是（2,2,2,3），存在子问题多次计算的情况。

3）简化后递推式的优势：

将所有情况都包含，且不重复计算，以i=9为例，最优解为（2,2,2,3）时，只会求解一次2和7，其中7可以分为（2,2,3）。而4和5的话只有5可以分为（2,3），4不可以分割。不存在原递推式的问题。

递推式更简单。

包含所有可能的情况。

三、钢条切割问题：自顶向下实现

1、原递推式代码实现

p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30] # 钢条不同长度价格，其索引即为钢条长度

# 未简化前递推式
def cut_rod_recurision_1(p, n):
    # 长度为0，钢条无价值
    if n == 0:
        return 0
    # 递归实现递推式
    else: 
        res = p[n] # 不切割，全局变量
        for i in range(1,n): # 递归的结束条件，循环次数为r1~rn-1
            # 递推式，递归的是不同的切割方法
            res = max(res,cut_rod_recurision_1(p, i) + cut_rod_recurision_1(p, n-i)) 
        return res
    
print(cut_rod_recurision_1(p,9))

输出结果：

2、简化后递推式实现

p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30] # 钢条不同长度价格，其索引即为钢条长度
# 简化后递推式
def cut_rod_recurision_2(p, n): # p是钢条不切割价格，n钢条长度
    # 长度为0，钢条无价值
    if n == 0:
        return 0
    # 简化后递推式
    else:
        res = 0 # 初始结果为0
        for i in range(1,n+1): # 从p1+rn-1到pn+r0，因此循环1~n。
            res = max(res, p[i] + cut_rod_recurision_2(p, n-i))  # 递推式
        return res
    
print(cut_rod_recurision_2(p,9))

输出结果：

3、对比两种递推式的运行时间

import time

# 时间装饰器
def cal_time(func):
    def wrapper(*args, **kwargs): #函数参数不确定的时候，用*args和**kwargs，前者叫位置参数，后者叫关键字参数。
        t1 = time.time()
        result = func(*args, **kwargs) #运行被装饰的函数
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__,t2-t1)) #func.__name__装饰器的函数，表示函数名称
        return result
    
    return wrapper

# p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30] # 钢条不同长度价格，其索引即为钢条长度
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]

# 未简化前递推式
def cut_rod_recurision_1(p, n):
    # 长度为0，钢条无价值
    if n == 0:
        return 0
    # 递归实现递推式
    else: 
        res = p[n] # 不切割，全局变量
        for i in range(1,n): # 递归的结束条件，循环次数为r1~rn-1
            # 递推式，递归的是不同的切割方法
            res = max(res,cut_rod_recurision_1(p, i) + cut_rod_recurision_1(p, n-i)) 
        return res

@cal_time
def c1(p,n): # 递归用语法糖会每层都运行，所以加个外壳
    return cut_rod_recurision_1(p,n)

print(c1(p,15))

# 简化后递推式
def cut_rod_recurision_2(p, n): # p是钢条不切割价格，n钢条长度
    # 长度为0，钢条无价值
    if n == 0:
        return 0
    # 简化后递推式
    else:
        res = 0 # 初始结果为0
        for i in range(1,n+1): # 从p1+rn-1到pn+r0，因此循环1~n。
            res = max(res, p[i] + cut_rod_recurision_2(p, n-i))  # 递推式
        return res

@ cal_time   
def c2(p, n):
    return cut_rod_recurision_2(p, n)
    
print(c2(p,15))

输出结果：

c1 running time: 1.8488576412200928 secs.
42
c2 running time: 0.01401066780090332 secs.
42

输出结果可知，原递推式的运行时间比简化后运行时间长。

原递推式每次都会递归2次，简化后的地递推式每次递归1次。

4、自顶向下递归实现的复杂度

递归求解钢条切割问题即为自顶向下求解，为何实现的效率为这么差？

1）即使是简化后的递推式，递归1次，但仍然存在重复子问题的计算。例如：求解r8时，其中p1+r7，p2+r6，...,p8+r0，r7求解又需要p1+r6，...，p7+r0。此时的r6以及被重复计算了，r5，r4重复计算的次数更多。也就是说在递归的过程中，存在大量的子问题重读计算。

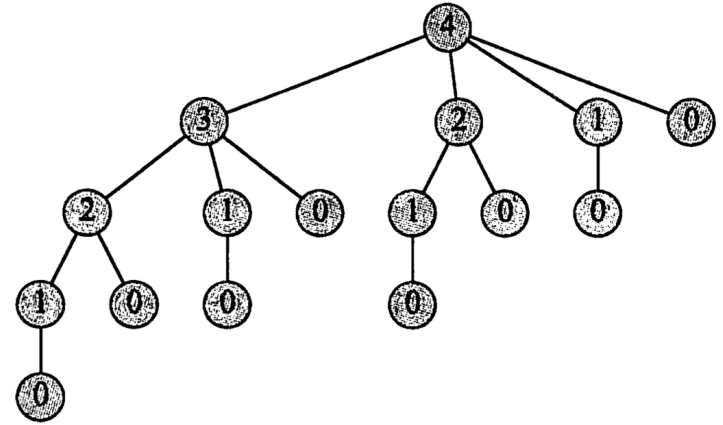
2）如下图所示，求r4需要计算r0，r1，r2，r3；求解r3，需要r2，r1，r0；求解r2需要r1，r0。可以发现r2重复计算2次，r1重复计算4次。

时间复杂度为 $\text{[math]}$ 。

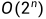四、钢条切割问题:自底向上的实现

1、动态规划解法

观察自顶向下的递归求解，存在重复求解相同的子问题，效率极低，因此提出动态规划的解法。

动态规划的思想：

每个子问题只求解一次，保存求解结果

之后需要此问题时，只需查找保存的结果

2、自底向上代码实现-动态规划

import time

# 时间装饰器
def cal_time(func):
    def wrapper(*args, **kwargs): #函数参数不确定的时候，用*args和**kwargs，前者叫位置参数，后者叫关键字参数。
        t1 = time.time()
        result = func(*args, **kwargs) #运行被装饰的函数
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__,t2-t1)) #func.__name__装饰器的函数，表示函数名称
        return result
    
    return wrapper

# p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30] # 钢条不同长度价格，其索引即为钢条长度
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]

@cal_time
def cut_rod_dp(p, n):
    r = [0] # n=0时，r为0
    for i in range(1, n+1): # 需要求解r1~rn，因此循环1~n
        res = 0  # ri的初始值为0
        for j in range(1, i+1): # n=i时，ri = max(p1+ri-1,...,pi+r0),每个ri循环j从1~i
            res = max(res, p[j] + r[i-j])  # 每个子问题求解
        r.append(res) # 每个ri存储到列表中方便取用
    return r[n]  

print(cut_rod_dp(p,20))

结果输出

cut_rod_dp running time: 0.0 secs.
56

3、与递归求解运行时间对比

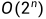动态规划求解时间复杂度为 $\text{[math]}$ ,而递归求解最小时间复杂度为 $\text{[math]}$ ,时间复杂度小于递归求解。

如下图所示：求解r4时，需要r3，r2，r1，r0都已经存在列表中，可直接取用，不需要再进行运算，大大减少了计算复杂度。

五、钢条切割问题：重构解

1、重构解问题

（1）问题描述

如何修改动态规划算法，使其不仅输出最优解，还输出最优切割方案?

（2）解题思路

根据简化后的递推式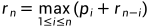 $\text{[math]}$ ，其中左边部分不再切割，右边部分可以再切割。

对每个子问题，保存切割一次时左边切下的长度，即不再切割的部分，定义为s[i]。

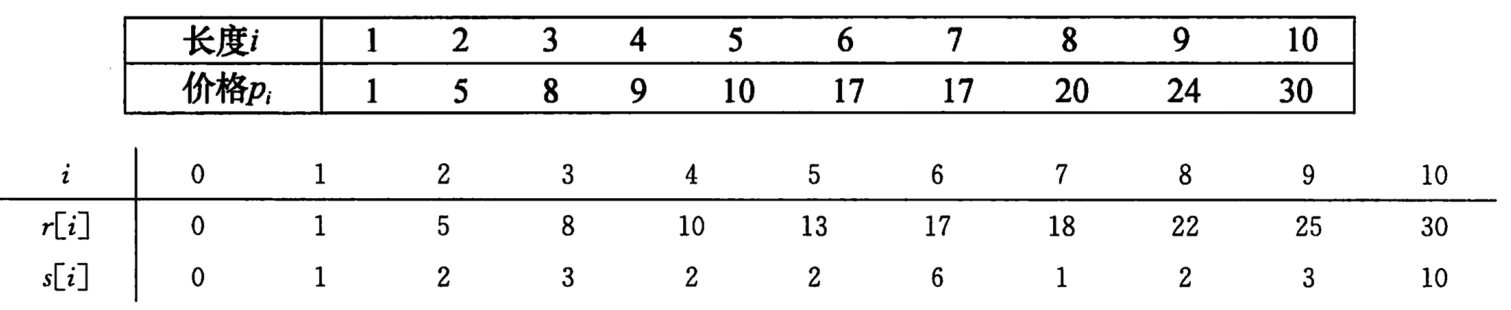
说明：i= 5时，r[5]=13,左边为2，右边为3。此时，左边的2不再分割，保存s[5]=2，而右边的3还可以再分割，转化为i=3的问题。当i=3时，已知s[3]=3,则左边为3，右边为0,结束切割。且长度5的钢条切割方案为[2,3]。

（3）代码实现

# p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30] # 钢条不同长度价格，其索引即为钢条长度
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]

def cut_rod_extend(p,n): # 求解ri，si
    r = [0] # ri列表，i=0时，价值为0
    s = [0]  # si列表，i=0时，左侧切割长度为0
    for i in range(1,n+1): # 求解r1~rn的n个解
        res_r = 0  # ri的值，表示最大收益
        res_s = 0  # si的值，价格最大值对应方案左边不切割的长度
        for j in range(1,i+1):  #长度为i的最高价值ri = max(p1+ri-1,...,pi+r0),所以对比1~i个解的大小
            if p[j] + r[i-j] > res_r:  # 对比大小
                res_r = p[j] + r[i-j]
                res_s = j  # 对应的p[j]，即左边长度
        r.append(res_r) # ri结果存储至列表
        s.append(res_s) # si结果存储至列表

    return r[n],s # rn的最大价值，s是左边不在切割的长度列表

def cut_rod_solution(p,n): # 求解具体切割方案
    r, s = cut_rod_extend(p,n) # 得到r，s列表
    ans = [] # 切割方案列表
    while n > 0: # 当钢条还有长度时，循环
        ans.append(s[n]) # 将n最大收益时左边不切割的长度存储到方案列表
        n -= s[n] # 钢条右边可继续切割的长度为n-sn
    return ans


r,s = cut_rod_extend(p, 15)    # 最大收益值，及最大收益时左边不再切割部分长度列表
ans = cut_rod_solution(p, 15) # 最优切割方案
print(s)
print(r)
print(ans)

输出结果

[0, 1, 2, 3, 2, 2, 6, 1, 2, 3, 2, 2, 6, 1, 2, 3]
42
[3, 6, 6]

2、动态规划问题关键特征

（1）动态规划方法的应用问题

存在且找到最优子结构，最优化问题

原问题的最优解中涉及多少个子问题

在确定最优解使用哪些子问题时，需要考虑多少种选择

能用递归求解的问题就能用动态规划求解

重叠子问题

递归求解时子问题被重复计算

Python数据结构与算法-动态规划（钢条切割问题）

一、动态规划（DP）介绍

1、从斐波那契数列看动态规划

（1）问题

（2）递归方法的代码实现

（3）非递归方法代码实现

（4）动态规划简单理解

二、钢条切割问题

1、提出问题

2、问题分析

（1）钢条切割方案举例

（2）问题求解思路

（3）钢条切割问题-递推式

（4）最优子结构-钢条切割问题

（5）最优子结构的简化

三、钢条切割问题：自顶向下实现

1、原递推式代码实现

2、简化后递推式实现

3、对比两种递推式的运行时间

4、自顶向下递归实现的复杂度

四、钢条切割问题:自底向上的实现

1、动态规划解法

2、自底向上代码实现-动态规划

3、与递归求解运行时间对比

五、钢条切割问题：重构解

1、重构解问题

（1）问题描述

（2）解题思路

（3）代码实现

2、动态规划问题关键特征

（1）动态规划方法的应用问题

相关文章