目录
1、(最大数的出现)编写程序读取整数,找出它们中的最大值,然后计算它的出现次数。假设输入以数字0结束。假设你输入的是“352555 0";程序找出的最大数是5,而5的出现次数是4。(提示:维护两个变量max和 count。变量max存储的是当前最大数,而count存储的是它的出现次数。初始状态下,将第一个值赋值给max,将1赋值给count。将max和每个随后的数字进行比较。如果这个数字大于max,就将它赋值给max且将count重置为1。如果这个数等于max,给count自增1。
2.将十进制数转换为二进制
3.将十进制数转换为十六进制
5.(显示闰年)编写程序显示21世纪(从2001年到2100年)里所有的闰年,每行显示10个闰年。这些年被一个空格隔开。
6.编写一个函数,计算一个整数各个数字之和,例如999返回的值应为27(9+9+9)
7.编写一个整数,输出其反向数字
8.(摄氏度和华氏度之间的转换)
9.(数列求和)编写一个函数计算下面的数列。
10.平方根的近似求法)math模块里有几种实现sqrt函数的方法。其中一种方法就是巴比伦函数。它通过重复地使用下面的公式计算求出n的平方根的近似值。
11.(回文素数)回文素数是指一个数既是素数又是回文数。例如,131既是素数也是回文数。数字313和717都是如此。编写程序显示前100个回文素数。每行显示10个数字,并且准确对齐。
1、(最大数的出现)编写程序读取整数,找出它们中的最大值,然后计算它的出现次数。假设输入以数字0结束。假设你输入的是“352555 0";程序找出的最大数是5,而5的出现次数是4。(提示:维护两个变量max和 count。变量max存储的是当前最大数,而count存储的是它的出现次数。初始状态下,将第一个值赋值给max,将1赋值给count。将max和每个随后的数字进行比较。如果这个数字大于max,就将它赋值给max且将count重置为1。如果这个数等于max,给count自增1。
max_num = None
count = 0
while True:
a = input("输入整数,以0结束:")
if a == '0':
break
if max_num is None or a > max_num:
max_num = a
count = 1
elif a == max_num:
count += 1
print(f"最大数为{max_num}")
print(f"出现的次数为:{count}")
2.将十进制数转换为二进制
a = int(input("输入一个十进制的数字吧~"))
print(f"二进制为{bin(a)}")
3.将十进制数转换为十六进制
a = int(input("输入一个十进制的数字吧~"))
print(f"二进制为{hex(a)}")
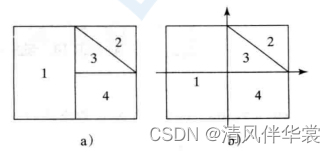
4.(蒙特卡罗模拟)一个正方形被分为四个更小的区域,如图a所示。如果你投掷一个飞塾到这个正方形一百万次,这个飞镖落在一个奇数区域里的概率是多少?编写程序模拟这个过程然后显式结果。(提示:将这个正方形的中心放在坐标系统的中心位置,如图b所示。在正方形中随机产生一个点,然后统计这个点落入奇数区域的次数。
import random
count = 0
for i in range(1000000):
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
if x < 0 or (x > 0 and y > 0 and x + y <= 1):
count += 1
res = count / 1000000
print("落在奇数区域的概率为:", res)

5.(显示闰年)编写程序显示21世纪(从2001年到2100年)里所有的闰年,每行显示10个闰年。这些年被一个空格隔开。
count = 0
for i in range(2001,2100):
if i % 4 == 0:
print(i,end=' ')
count += 1
if count % 10 == 0:
print()
6.编写一个函数,计算一个整数各个数字之和,例如999返回的值应为27(9+9+9)
def sumDigits(n):
return 0 if n == 0 else n%10+sumDigits(n//10)
n = int(input("输入一个数字"))
print(f"各位数字和为:{sumDigits(n)}")
7.编写一个整数,输出其反向数字
a = input("输入一个整数:")
print(a[::-1])
8.(摄氏度和华氏度之间的转换)
def fahrenheit_to_celsius(fahrenheit):
celsius = (5 / 9) * (fahrenheit - 32)
return round(celsius, 2)
def celsius_to_fahrenheit(celsius):
fahrenheit = (9 / 5) * celsius + 32
return round(fahrenheit, 2)
print("------------------")
print("摄氏度\t华氏度")
print("------------------")
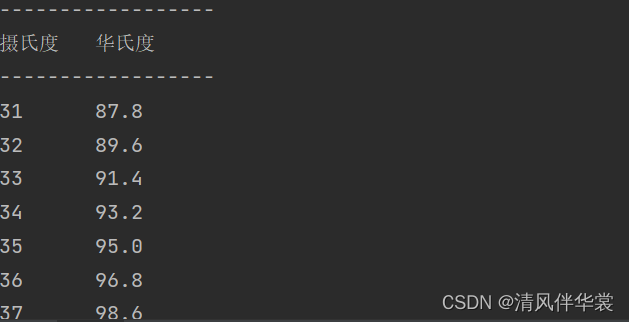
for c in range(31,41):
f = celsius_to_fahrenheit(c)
print(f"{c}\t\t{f}")
print("------------------")
print("华氏度\t摄氏度")
print("------------------")
for f in range(30,120,10):
c = fahrenheit_to_celsius(f)
print(f"{f}\t\t{c}")
9.(数列求和)编写一个函数计算下面的数列。

total = 0
for i in range(1, n + 1):
total += i / (i + 1)
return total
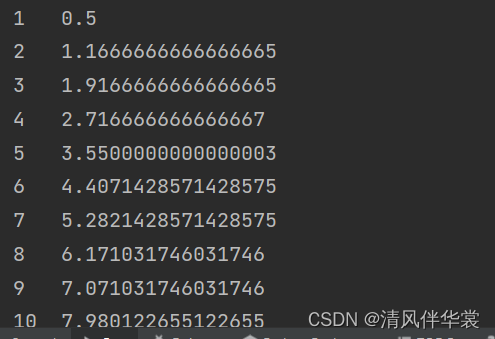
for j in range(1, 21):
s = sum_m(j)
print(f"{j}\t{s}")
10.平方根的近似求法)math模块里有几种实现sqrt函数的方法。其中一种方法就是巴比伦函数。它通过重复地使用下面的公式计算求出n的平方根的近似值。
nextGuess - (1astGuess +(n/ lastGuess)) /2
当nextGuess和 lastGuess很接近时,nextGuess就是平方根的近似值。初始的猜测值可以是任意的正数(例如:1)。这个值将是lastGuess 的开始值。如果nestGuess和 lastGuess的差别非常小时,例如:0.0001,你可以说nestGuess就是n的平方根近似值。否则,nextGuess 就变成lastGuess,这个近似过程继续。实现下面的函数返回n的平方根。
def sqrt(n):
lastGuess = 1
nextGuess = (lastGuess + n / lastGuess) / 2
while (nextGuess - lastGuess) > 0.0001 or (lastGuess - nextGuess) > 0.0001:
lastGuess = nextGuess
nextGuess = (lastGuess + n / lastGuess) / 2
print(nextGuess)
sqrt(49) ![]()
11.(回文素数)回文素数是指一个数既是素数又是回文数。例如,131既是素数也是回文数。数字313和717都是如此。编写程序显示前100个回文素数。每行显示10个数字,并且准确对齐。
def is_zhishu(num):
for i in range(2, num // 2 + 1):
if num % i == 0:
return False
return True
def is_huiwenshu(num):
if str(num) == str(num)[::-1]:
return True
count = 0
num = 2
while count < 100:
if is_zhishu(num) and is_huiwenshu(num):
print("%5d" % num, end=" ")
count += 1
if count % 10 == 0:
print()
num += 1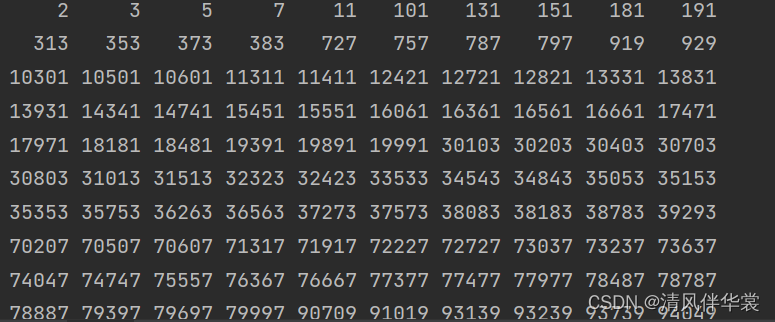




![[python][学习]turtle.circle()函数](https://img-blog.csdnimg.cn/img_convert/2d35173b367d43ad86c5dbf40ca91167.png)