问题 A: 最小平均等待时间
题目描述
有n个顾客同时在等待一项服务,顾客i需要的服务时间为ti,1≤i≤n。要安排一个服务次序使得平均等待时间最小(平均等待时间是n个顾客等待服务时间的总和除以n)。请编写算法,计算最小平均等待时间。
输入
第一行为测试用例个数m,m≤1000。 第二行开始为m个测试用例,每个测试用例由一组空格间隔的整数组成,第一个整数n为顾客的人数,后面n个整数为每个顾客需要的服务时间t,0<m≤1000,0<t≤1000。
输出
对每个测试用例,输出最小平均等待时间的整数部分(舍去小数部分),每个输出占一行。
样例输入 复制
2
5 15 9 3 14 3
10 13 3 12 9 6 9 1 91 44 32
样例输出 复制
10
36欸,这不就是短作业优先的调度算法嘛
#include<bits/stdc++.h>
using namespace std;
int main() {
int t;
cin>>t;
while(t--){
int n;
cin>>n;
int a[n];
for(int i=0; i<n; i++)
cin>>a[i];
sort(a,a+n);
int sum=0;
int ans=0;
for(int i=1; i<n; i++) {
sum+=a[i-1];
ans+=sum;
}
cout<<ans/n<<endl;
}
return 0;
}问题 B: 最少货币支付问题
题目描述
现行的货币体系为(1、2、5、10、20、50、100),请设计算法,计算要用最少的货币数支付指定金额N,每种货币需要使用的数量。
输入
第一行为测试用例个数n,n≤1000。 后面n行,每行为一个测试用例,每个测试用例为一个大于0的整数目标金额m,0≤m≤10000。
输出
对每个测试用例,输出一行由空格间隔的7个整数,分别表示1元、2元、5元、10元、20元、50元、100元所使用的数量。
样例输入 复制
2
15
189
样例输出 复制
0 0 1 1 0 0 0
0 2 1 1 1 1 1
#include<bits/stdc++.h>
int main()
{
int n,N;
scanf("%d",&N);
while(N--)
{
int a=0,b=0,c=0,d=0,e=0,f=0,g=0;
scanf("%d",&n);
while(n>=100)
{
g=g+1;
n=n-100;
}
while(n>=50&&n<100)
{
f=f+1;
n=n-50;
}
while(n>=20&&n<50)
{
e=e+1;
n=n-20;
}
while(n>=10&&n<20)
{
d=d+1;
n=n-10;
}
while(n>=5&&n<10)
{
c=c+1;
n=n-5;
}
while(n>=2&&n<5)
{
b=b+1;
n=n-2;
}
if(n>0&&n<2)
{
a=1;
}
printf("%d %d %d %d %d %d %d\n",a,b,c,d,e,f,g);
}
} 问题 C: 活动安排
题目描述
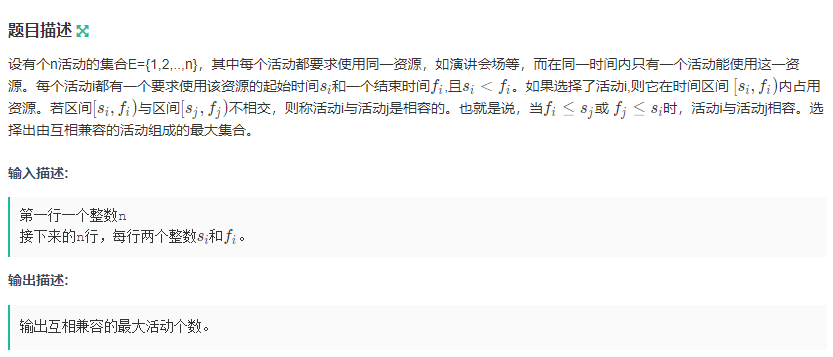
输
样例输入
4
1 3
4 6
2 5
1 7样例输出
2提示
1≤n≤1000
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define INF 0x3f3f3f3f
struct ac {
int start;
int end;
};
bool cmp(ac a, ac b){
return a.end < b.end;
}
int main(){
int n;
cin >> n;
ac a[1005];
for (int i = 0; i < n; i++){
cin >> a[i].start >> a[i].end;
}
sort(a, a + n, cmp);
int ans = 1;
int k = a[0].end;
int loc = 0;
for (int i = 1; i < n; i++){
if (a[i].start >= a[loc].end){
ans++;
k=a[i].end;
loc = i;
}
}
cout << ans << endl;
}问题 D: 数列极差
题目描述
小源的老师在黑板上写了一个由n个正整数组成的数列,要求小源进行如下操作:每次擦去其中的两个数a和b,然后在数列中加入一个数 a*b+1,如此下去直至黑板上剩下一个数为止,在所有按这种操作方式最后得到的数中,最大的为max,最小的为min, 则该数列的极差定义为 M=max-min.
由于小源忙于准备期末考试,现请你帮助她,对于给定的数列,计算出相应的极差M。
输入
第一行为一个正整数n表示正整数序列的长度;
在接下来的n行中,每行输入一个正整数。
接下来的一行有一个0,表示数据结束。
输出
输出只有一行,为相应的极差d。
样例输入 复制
3
1
2
3
0样例输出 复制
2提示
对于全部数据,0≤n≤50000,保证所有数据计算均在 32 位有符号整数范围内。
#include <bits/stdc++.h>
#define rush() int T;cin>>T;while(T--)
#define go(a) while(cin>>a)
#define ms(a,b) memset(a,b,sizeof a)
#define E 1e-8
#define debug(a) cout<<"*"<<a<<"*"<<endl
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<double,double> Pair;
const int inf=0x3f3f3f3f;
const int N=1e4+5;
int n,m,t;
int i,j,k;
//int a[N];
priority_queue<int,vector<int>,greater<int> >maxx;
priority_queue<int,vector<int>,less<int> >minn;
int main()
{
IOS;
while(cin>>n){
for(i=0;i<n;i++){
int x; cin>>x;
maxx.push(x); minn.push(x);
}
int a,b;
while(maxx.size()>1){
a=maxx.top(); maxx.pop();
b=maxx.top(); maxx.pop();
maxx.push(a*b+1);
}
while(minn.size()>1){
a=minn.top(); minn.pop();
b=minn.top(); minn.pop();
minn.push(a*b+1);
}
cout<<maxx.top()-minn.top()<<endl; break;
}
return 0;
}问题 E: 钓鱼
题目描述
在一条水平路边,有n个钓鱼湖,从左到右编号为1,2,…,n。庄dalao有H个小时的空余时间,他希望利用这个时间钓到更多的鱼。他从1出发,向右走,有选择的在一些湖边停留一定的时间(是5分钟的倍数)钓鱼。最后在某一个湖边结束钓鱼。庄dalao从第i个湖到第i+1个湖需要走5×Ti分钟路,还测出在第i个湖停留,第一个5分钟可以钓到Fi条鱼,以后每再钓5分钟,可以钓到的鱼量减少Di,若减少后的鱼量小于0,则减少后的鱼量为0。为了简化问题,庄dalao假定没有其他人钓鱼,也没有其他因素影响他钓到期望数量的鱼。请编程求出庄dalao最多能钓鱼的数量。
输入
第一行一个整数n,表示湖的个数,不大于25
第二行一个整数H,表示庄dalao的空闲时间,不大于20
第三行有n个整数,依次表示每个湖第一个5分钟能钓到鱼的数量 ,不大于100
第四行有n个整数,依次表示以后的每5分钟钓鱼数量比前一个5分钟钓鱼数量减少的数量
第五行有n-1个整数,Ti表示由第i个湖到第i+1个湖需要花5×Ti分钟的路程
保证在int以内
输出
输出只有一行,表示庄dalao最多能钓鱼的数量。
样例输入 复制
3
1
4 5 6
1 2 1
1 2样例输出 复制
35提示

#include <bits/stdc++.h>
#define rush() int T;cin>>T;while(T--)
#define go(a) while(cin>>a)
#define ms(a,b) memset(a,b,sizeof a)
#define E 1e-8
#define debug(a) cout<<"*"<<a<<"*"<<endl
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define s first
#define e second
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> Pair;
const int inf=0x3f3f3f3f;
const int N=1e3+5;
int n,m,t;
int i,j,k;
int fish[N],d[N],dis[N];
priority_queue< Pair >q;
int main()
{
IOS; string s;
int n;
cin>>n;
int t; cin>>t; t*=60;
for(i=1;i<=n;i++) cin>>fish[i];
for(i=1;i<=n;i++) cin>>d[i];
for(i=2;i<=n;i++) cin>>dis[i];
int ans=-1,waste=0;
for(i=1;i<=n;i++){
int maxx=0;
for(j=1;j<=i;j++){
q.push(make_pair(fish[j],j));
}
int rest=t-waste;
while(rest>0&&q.top().first>0){
Pair p=q.top(); q.pop();
maxx+=p.first;
p.first-=d[p.second];
q.push(p);
rest-=5;
}
ans=max(maxx,ans);
waste+=dis[i+1]*5;
while(!q.empty()) q.pop();
}
cout<<ans<<endl;
return 0;
}问题 F: N后问题(回溯法)
题目描述
在N*N的类似国际象棋棋盘上,要放置N个王后,要求任两个王后之间不能互相攻击,也就是任两个王后不共线。 问有多少种摆放的方法?
输入
输入为一组整数,每行为一个整数n,n<=10,最后一行是一个0。
输出
对每个整数n(不包括结尾行的0),计算摆放王后的方法,并输出方案个数,每个输出占一行。
样例输入 复制
2
4
0
样例输出 复制
0
2#include<iostream>
#include <cmath>
using namespace std;
int N;
int ans=0;
int colqueen[1000];
void NQueen(int k);
int main()
{
while(cin >> N){
ans=0;
if(N==0)
break;
int k=0;
NQueen(k);
cout<<ans<<endl;
}
return 0;
}
void NQueen(int k)
{
if(k==N)
{
ans++;
return;
}
for(int i=0;i<N;i++)//列
{
int j;
for(j=0;j<k;j++)//row
{
if(colqueen[j]==i||fabs(colqueen[j]-i)==fabs(k-j))
{
break;
}
}
if(j==k)
{
colqueen[k]=i;
NQueen(k+1);
}
}
}


![[python][学习]turtle.circle()函数](https://img-blog.csdnimg.cn/img_convert/2d35173b367d43ad86c5dbf40ca91167.png)




![[oeasy]python0132_变量含义_meaning_声明_declaration_赋值_assignment](https://img-blog.csdnimg.cn/img_convert/7e5a3fb4bfbb930f05b1a194be5ba21f.png)