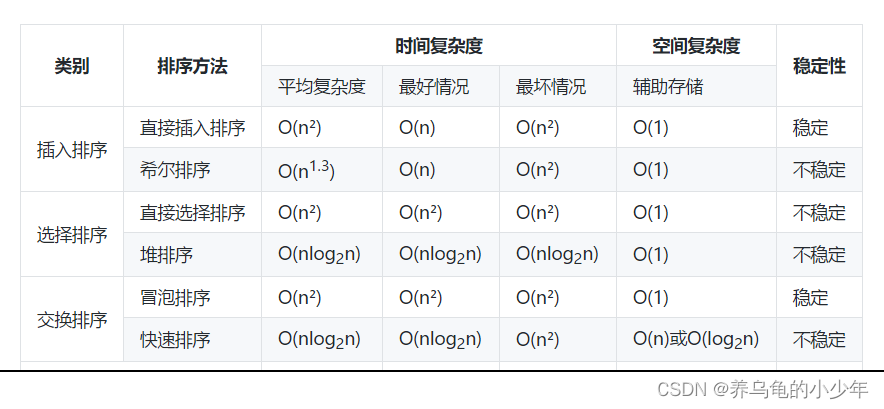
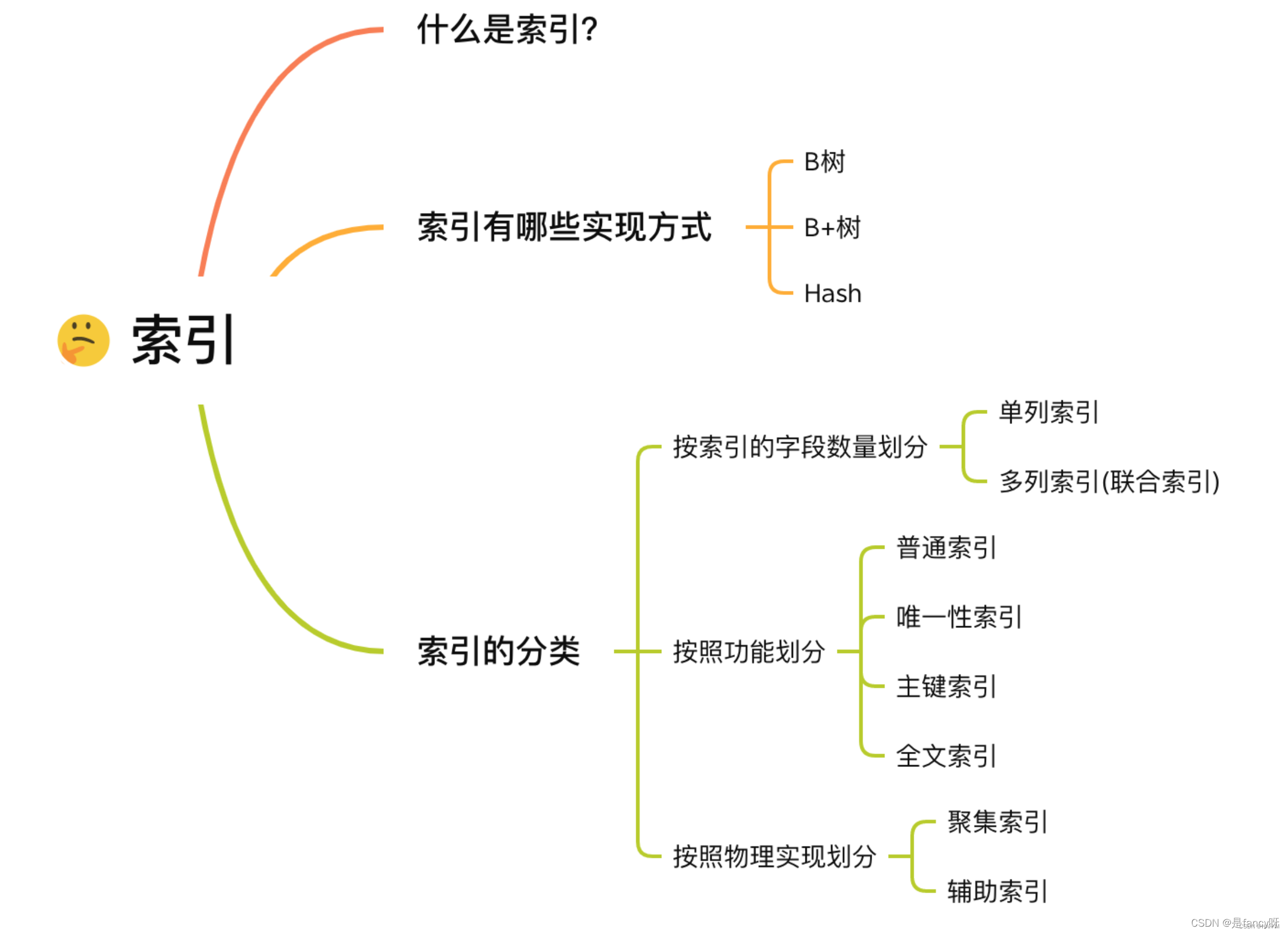
数据结构——二叉搜索树

一、二叉搜索树
- 1.二叉搜索树的特性
- 2.二叉搜索树的查找、插入和删除
二、平衡二叉树
- 1.基本介绍
- 2.AVL树的自平衡
- - 1）自平衡的调整操作
  - 2）自平衡调整的局面
- 3.AVL树的代码实现
- 4.AVL树的特点
三、红黑树
- 1.基本介绍
- 2.红黑树的自平衡
- - 1）是否破坏平衡
  - 2）自平衡的调整操作
- 3.红黑树的插入
- - 1）局面1
  - 2）局面2
  - 3）局面3
  - 4）局面4
  - 5）局面5
- 4.红黑树的删除
- - 1）step1
  - 2）step2
  - 3）step3
- 5.红黑树的实现
- 6.AVL树和红黑树的对比选用

一、二叉搜索树

1.二叉搜索树的特性

在二叉搜索树中，每个结点的数值比左子树上的每个结点都大，比所有右子树上的结点都小。是一个有数值的有序树。
若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树

二叉搜索树可用于查找，对于一个节点分布相对平衡的二叉搜索树，如果节点总数是n，查找节点的时间复杂度为 $O(\log n)$ ，和树的深度成正比。

但如果二叉搜索树出现节点分布极端不均的情况，如绝大多数节点都集中在左子树上，查找节点的时间复杂度就会退化成 $O (n)$ 。

二叉搜索树还可维持节点的有序性，进行插入、删除操作后始终保持有序。中序遍历二叉搜索树会得到一个有序的序列。

2.二叉搜索树的查找、插入和删除

二、平衡二叉树

1.基本介绍

平衡二叉树是一种特殊的二叉搜索树，其中每一个节点的左子树和右子树的高度差至多等于1。也被称为AVL树。

平衡二叉树可以在每次插入、删除节点后进行自平衡调整，重新达到平衡状态。

二叉树上节点的左子树高度和右子树高度的差值称为平衡因子BF（Balance Factor），平衡二叉树上所有节点的平衡因子只可能是-1、0、1，才是保持高度平衡，否则就不平衡。

2.AVL树的自平衡

1）自平衡的调整操作

AVL树提供了两种特殊的操作来进行自平衡：

1、左旋
逆时针旋转AVL树的两个节点，使父节点被自己的右孩子取代，而原父节点成为自己原来位置节点的左孩子。
（空心三角形代表着节点下面的子树。）
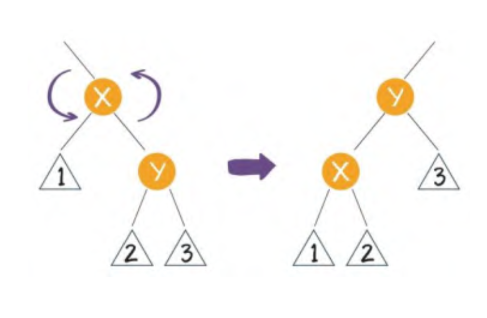
在这里插入图片描述
2、右旋
逆时针旋转AVL树的两个节点，使父节点被自己的左孩子取代，而原父节点成为自己原来位置节点的右孩子。

2）自平衡调整的局面

AVL树的调整分成4种局面：

1、左左局面（LL）
在这里插入图片描述
祖父节点A有一个左孩子节点B，B又有一个左孩子节点C

在这种局面下，以A为轴，进行右旋操作
在这里插入图片描述 2、右右局面（RR）

祖父节点A有一个右孩子节点B，B又有一个右孩子节点C

在这种局面下，以A为轴，进行左旋操作
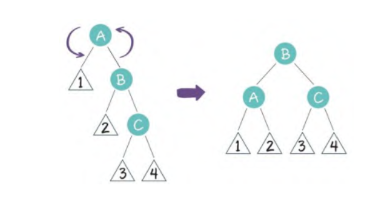
在这里插入图片描述
3、左右局面（LR）

祖父节点A有一个左孩子节点B，B又有一个右孩子节点C

在这种局面下，先以B为轴，进行左旋操作
在这里插入图片描述
这样就转化为了左左局面，继续以A为轴，进行右旋操作

3、右左局面（RL）

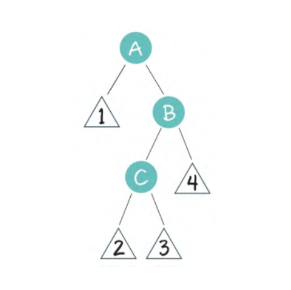
祖父节点A有一个右孩子节点B，B又有一个左孩子节点C

在这种局面下，先以B为轴，进行右旋操作
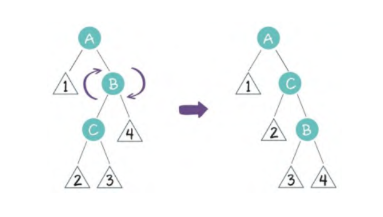
在这里插入图片描述
这样就转化为了右右局面，继续以A为轴，进行左旋操作

在平衡二叉树中插入或删除节点时，可能会打破平衡，使子树出现如上4种局面。这时就需要进行相应的操作调整。

3.AVL树的代码实现

public class AVLTree {
    private TreeNode root;
    /*
     * 获取树的高度
     */
    private int height(TreeNode node) {
        if (node != null)
            return node.height;
        return 0;
    }
    public int height() {
        return height(root);
    }
    //查找结点
    public TreeNode search(TreeNode node, int data) {
        while (node!=null) {
            if (data < node.data)
                node = node.left;
            else if (data > node.data)
                node = node.right;
            else
                return node;
        }
        return node;
    }
    //左左局面旋转
    private TreeNode leftLeftRotation(TreeNode node) {
        //leftChildNode 对应示意图中的结点B
        TreeNode leftChildNode = node.left;
        node.left = leftChildNode.right;
        leftChildNode.right = node;
        //刷新结点A和结点B的高度
        node.height = Math.max(height(node.left), height(node.right)) + 1;
        leftChildNode.height = Math.max(height(leftChildNode.left), node.height) + 
        //返回旋转后的父结点
        return leftChildNode;
    }
    //右右局面旋转
    private TreeNode rightRightRotation(TreeNode node) {
        //rightChildNode 对应示意图中的结点B
        TreeNode rightChildNode = node.right;
        node.right = rightChildNode.left;
        rightChildNode.left = node;
        //刷新结点A和结点B的高度
        node.height = Math.max(height(node.left), height(node.right)) + 1;
        rightChildNode.height = Math.max(height(rightChildNode.right), node.height)
        //返回旋转后的父结点
        return rightChildNode;
    }
    //左右局面旋转
    private TreeNode leftRightRotation(TreeNode node) {
        //先做左旋
        node.left = rightRightRotation(node.left);
        //再做右旋
        return leftLeftRotation(node);
    }
    //右左局面旋转
    private TreeNode rightLeftRotation(TreeNode node) {
        //先做右旋
        node.right = leftLeftRotation(node.right);
        //再做左旋
        return rightRightRotation(node);
    }
    //插入结点
    public void insert(int data) {
        root = insert(root, data);
    }
    //插入结点详细过程（递归）
    private TreeNode insert(TreeNode node, int data) {
        if (node == null) {
            node = new TreeNode(data);
        } else {
            if (data < node.data) {
                //新结点小于当前结点，选择当前结点的左子树插入
                node.left = insert(node.left, data);
                // 插入节点后，若AVL树失去平衡，则进行相应的调节。
                if (node.getBalance() == 2) {
                    if (data < node.left.data) {
                        node = leftLeftRotation(node);
                    } else {
                        node = leftRightRotation(node);
                    }
                }
            } else if (data > node.data)  {
                //新结点大于当前结点，选择当前结点的右子树插入
                node.right = insert(node.right, data);
                // 插入节点后，若AVL树失去平衡，则进行相应的调节。
                if (node.getBalance() == -2) {
                    if (data > node.right.data) {
                        node = rightRightRotation(node);
                    } else {
                        node = rightLeftRotation(node);
                    }
                }
            } else {
                System.out.println("AVL树中已有重复的结点！");
            }
        }
        //刷新结点的高度
        node.height = Math.max(height(node.left), height(node.right)) + 1;
        return node;
    }
    //删除结点
    public void remove(int data) {
        TreeNode deletedNode;
        if ((deletedNode = search(root, data)) != null)
            root = remove(root, deletedNode);
    }
    //删除结点详细过程（递归）
    private TreeNode remove(TreeNode node, TreeNode deletedNode) {
        // 根为空 或者 没有要删除的节点，直接返回null。
        if (node==null || deletedNode==null)
            return null;
        if (deletedNode.data < node.data){
            //待删除结点小于当前结点，在当前结点的左子树继续执行
            node.left = remove(node.left, deletedNode);
            // 删除节点后，若AVL树失去平衡，则进行相应的调节。
            if (height(node.right) - height(node.left) == 2) {
                TreeNode r =  node.right;
                if (height(r.left) > height(r.right))
                    node = rightLeftRotation(node);
                else
                    node = rightRightRotation(node);
            }
        } else  if (deletedNode.data > node.data) {
            //待删除结点大于当前结点，在当前结点的右子树继续执行
            node.right = remove(node.right, deletedNode);
            // 删除节点后，若AVL树失去平衡，则进行相应的调节。
            if (height(node.left) - height(node.right) == 2) {
                TreeNode l =  node.left;
                if (height(l.right) > height(l.left))
                    node = leftRightRotation(node);
                else
                    node = leftLeftRotation(node);
            }
        } else {
            // tree的左右孩子都非空
            if ((node.left!=null) && (node.right!=null)) {
                if (height(node.left) > height(node.right)) {
                    // 如果node的左子树比右子树高，找出左子树最大结点赋值给Node，并删除最小结点
                    TreeNode max = maximum(node.left);
                    node.data = max.data;
                    node.left = remove(node.left, max);
                } else {
                    // 如果node的右子树比左子树高，找出右子树最小结点赋值给Node，并删除最小结点
                    TreeNode min = minimum(node.right);
                    node.data = min.data;
                    node.right = remove(node.right, min);
                }
            } else {
                node = (node.left!=null) ? node.left : node.right;
            }
        }
        node.height = Math.max(height(node.left), height(node.right)) + 1;
        return node;
    }
    //找出结点node为根的子树的最大节点
    private TreeNode maximum(TreeNode node) {
        if (node == null)
            return null;
        while(node.right != null)
            node = node.right;
        return node;
    }
    //找出结点node为根的子树的最小节点
    private TreeNode minimum(TreeNode node) {
        if (node == null)
            return null;
        while(node.left != null)
            node = node.left;
        return node;
    }
    //中序遍历
    public static void inOrderTraversal(TreeNode node) {
        if(node != null) {
            inOrderTraversal(node.left);
            System.out.print(node.data+" ");
            inOrderTraversal(node.right);
        }
    }
    //层序遍历
    public static void levelOrderTraversal(TreeNode root){
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            TreeNode node = queue.poll();
            System.out.print(node.data+" ");
            if(node.left != null){
                queue.offer(node.left);
            }
            if(node.right != null){
                queue.offer(node.right);
            }
        }
    }
    class TreeNode {
        int data;
        int height;
        TreeNode left;
        TreeNode right;
        public TreeNode(int data) {
            this.data = data;
            this.height = 0;
        }
        //获得结点的平衡因子
        public int getBalance(){
            int left =  (this.left==null ? 0:this.left.height);
            int right = (this.right==null ? 0:this.right.height);
            return left - right;
        }
    }
    public static void main(String[] args) {
        AVLTree tree = new AVLTree();
        int input[]= {5,3,7,2,4,6,9,1};
        for(int i=0; i<input.length; i++) {
            tree.insert(input[i]);
        }
        System.out.println("中序遍历: ");
        inOrderTraversal(tree.root);
        System.out.println();
        System.out.println("层序遍历: ");
        levelOrderTraversal(tree.root);
        System.out.println();
        System.out.printf("高度: %d\n", tree.height());
        int deletedData = 3;
        System.out.printf("删除根节点: %d\n", deletedData);
        tree.remove(deletedData);
        System.out.println("中序遍历: ");
        inOrderTraversal(tree.root);
        System.out.println();
        System.out.println("层序遍历: ");
        levelOrderTraversal(tree.root);
        System.out.println();
        System.out.printf("高度: %d\n", tree.height());
    }
}

4.AVL树的特点

AVL树在插入或删除节点时，每一层的相关节点都要修改自身的高度值，这使得AVL树的插入删除操作的平均时间复杂度成了 $O(n\log n)$ 。

AVL树维护的是绝对的平衡，这样查找效率较高，但维护成本也较高。

三、红黑树

1.基本介绍

红黑树和AVL树类似，也是为了维护二叉搜索树的平衡。

红黑树判断树平衡的方式要复杂一些，通过红色和黑色两种节点以及若干规则来判断平衡。

红黑树规则：

节点是红色或黑色
根节点是黑色
每个叶子节点都是黑色的空节点（NIL节点）
每个红色节点的子节点都是黑色（即不存在两个连续的红色节点）
从任意节点到其每个叶子节点的所有路径都包含相同数目的黑色节点

在这里插入图片描述
这些限制保证了红黑树的平衡性，红黑树从根节点到叶子节点的最长路径不会超过最短路径的2倍。

2.红黑树的自平衡

1）是否破坏平衡

当插入或删除节点的时候，红黑树的规则有可能被打破。这时候就需要做出一些调整，从而继续维持原有的规则。

1、未破坏平衡性：

向原红黑树插入值为14的新节点
在这里插入图片描述
**红黑树新插入的节点，默认是红色的。**由于父节点15是黑色节点，
因此这种情况并不会破坏红黑树的规则，无须做任何调整。

2、破坏平衡性：

向原红黑树插入值为21的新节点
在这里插入图片描述
由于父节点22是红色节点，因此这种情况打破了红黑树的规则4（每个红色节点的两个子节点都是黑色），必须进行调整，使之重新符合红黑树的规则。

2）自平衡的调整操作

1、旋转

旋转操作和AVL树基本相同。

2、变色

为了重新符合红黑树的规则，尝试把红色节点变为黑色，或者把黑色节点变为红色。

下图所表示的是红黑树的一部分（子树），新插入的节点Y是红色节点，它的父亲节点X也是红色的，不符合规则4，因此可以把节点X从红色变成黑色：
在这里插入图片描述
但是，仅仅把一个节点由红变黑，会导致相关路径凭空多出一个黑色节点，这样就打破了规则5。因此，我们还需要对其他节点做进一步的调整。

3.红黑树的插入

在红黑树中插入新节点的时候，可以分成5种不同的局面，每一种局面有不同的调整方法。

1）局面1

新节点A位于树根，没有父节点
在这里插入图片描述
这种局面，直接让新节点变色为黑色，规则2得到满足。同时，黑色的根节点使得每条路径上的黑色节点数目都增加了1，并没有打破规则5。

2）局面2

新节点B的父节点是黑色
在这里插入图片描述
这种局面，新插入的红色节点B并没有打破红黑树的规则，所以不需要做任何调整。

3）局面3

新节点D的父节点和叔叔节点都是红色
在这里插入图片描述
这种局面，两个红色节点B和D连续，违反了规则4。因此我们做如下调整：

让节点B变为黑色。
让节点A变为红色。
让节点C变为黑色。

4）局面4

新节点（D）的父节点是红色，叔叔节点是黑色或者没有叔叔，且新节点是父节点的右孩子，父节点（B）是祖父节点的左孩子。
在这里插入图片描述
以节点B为轴，做一次左旋转，使得新节点D成为父节点，原来的父节点B成为D的左孩子：

这样一来，进入了局面5。

如果局面4中的父节点B是右孩子，节点D是B的左孩子，则成为了局面4的镜像，原本的左旋操作改为右旋操作。
在这里插入图片描述

5）局面5

新节点（D）的父节点是红色，叔叔节点是黑色或者没有叔叔，且新节点是父节点的左孩子，父节点（B）是祖父节点的左孩子。
在这里插入图片描述
对于这种局面，做如下调整：

以节点A为轴，做一次右旋转，使得节点B成为祖父节点，节点A
成为节点B的右孩子。
让节点B变为黑色，节点A变为红色。

在这里插入图片描述
如果局面5中的父节点B是右孩子，节点D是B的右孩子，则成为了局面5的镜像，原本的右旋操作改为左旋操作。

4.红黑树的删除

1）step1

如果待删除节点有两个非空的孩子节点，转化成待删除节点只有一个孩子（或没有孩子）的情况。
在这里插入图片描述
假设节点8是待删除节点。由于节点8有两个孩子，我们选择仅大于8的节点10复制到8的位置，节点颜色变成待删除节点的颜色：

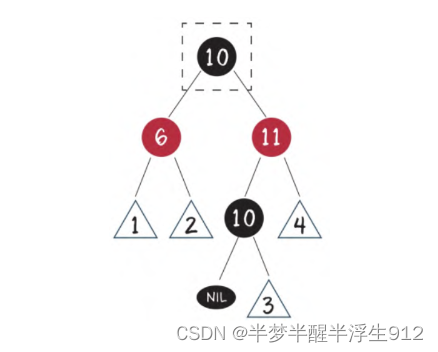
接下来我们需要删除原本的节点10（节点11的左子树）。

节点10能成为仅大于8的节点，必定没有左孩子节点，所以问题转换成了待删除节点只有一个右孩子（或没有孩子）的情况。接下来我们进入第2步。

2）step2

根据待删除节点和其唯一子节点的颜色，分不同局面来处理

局面1：自身是红色，子节点是黑色
这种情况最简单，按照二叉查找树的删除操作，删除节点1即可。
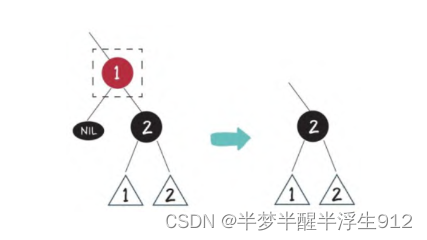
在这里插入图片描述

局面2：自身是黑色，子节点是红色

做如下调整：

删除节点1。
把节点2变成黑色节点（因为路径凭空减少了一个黑色节点）。

在这里插入图片描述
局面3：自身是黑色，子节点也是黑色，或者子节点是空叶子节点

这种情况最复杂，涉及很多变化。首先我们删除节点1：
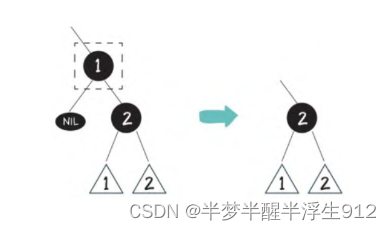
在这里插入图片描述
显然，这条路径上减少了一个黑色节点，而且节点2再怎么变色也解决不了问题。这时候我们进入第3步，专门解决父子双黑的情况。

3）step3

针对局面3这样的双黑节点情形，在删除父节点之后将会衍生出6种子局面，我们根据不同子局面做不同调整。

子局面1：节点2是红黑树的根节点
此时所有路径都减少了一个黑色节点，并未打破规则，不需要调整。

子局面2：节点2的父亲、兄弟、侄子节点都是黑色
此时，我们直接把节点2的兄弟节点B改为红色：
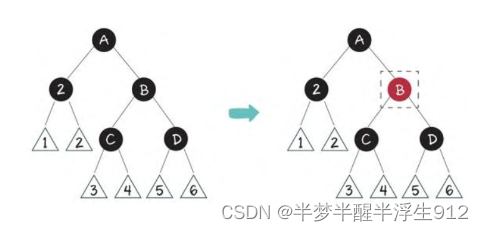
在这里插入图片描述
这样一来，原本节点2所在的路径少了一个黑色节点，现在节点B所在的路径也少了一个黑色节点，两边“扯平”了。可是，节点A以下的每一条路径都减少了一个黑色节点，与节点A之外的其他路径又造成了新的不平衡。对此，我们可以让节点A扮演原先节点2的角色，进行递归操作，重新判断各种情况。

子局面3：节点2的兄弟节点是红色

做如下调整：

以节点2的父节点A为轴，进行左旋。
节点A变成红色、节点B变成黑色。

在这里插入图片描述
这样的变化有可能转换成子局面4、5、6中的任意一种

子局面4：节点2的父节点是红色，兄弟和侄子节点是黑色

对于这种局面，我们直接让节点2的父节点A变成黑色，兄弟节点B变成红色：
在这里插入图片描述
这样一来，节点2的路径补充了黑色节点，而节点B的路径并没有减
少黑色节点，重新符合了红黑树的规则。

子局面5：节点2的父节点随意，兄弟节点B是黑色右孩子，左侄子节点是红色，右侄子节点是黑色

做如下调整：

以节点2的兄弟节点B为轴进行右旋。
节点B变为红色，节点C变为黑色。

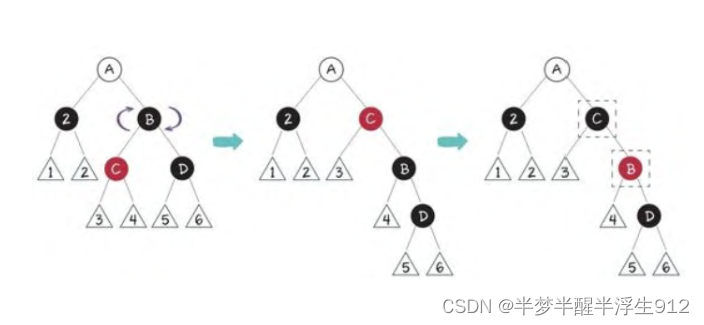
在这里插入图片描述
这样的变化转换成了子局面6。

子局面6：节点2的父节点随意，兄弟节点B是黑色右孩子，右侄子节点是红色

做如下调整：

以节点2的父节点A为轴左旋。
让节点A和节点B的颜色交换，并且节点D变为黑色。

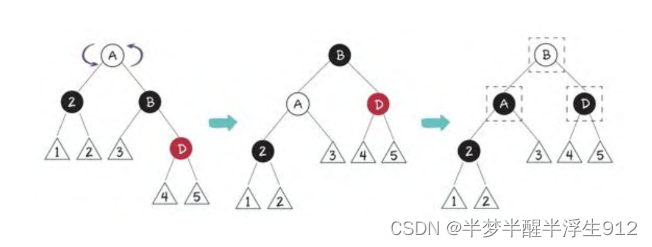
在这里插入图片描述
经过节点2的路径由（随意+黑）变成了（随意+黑+黑），补充了一个黑色节点；经过节点D的路径由（随意+黑+红）变成了（随意+黑），黑色节点并没有减少。所以，这时候重新符合了红黑树的规则。

5.红黑树的实现

import java.util.LinkedList;
import java.util.Queue;

public class RedBlackTree {
    TreeNode root;
    final static boolean RED = true;
    final static boolean BLACK = false;

    //查找结点
    public TreeNode search(int data) {
        TreeNode tmp = root;
        while (tmp != null) {
            if (tmp.data == data)
                return tmp;
            else if (tmp.data > data)
                tmp = tmp.left;
            else
                tmp = tmp.right;
        }
        return null;
    }

    //插入结点
    public boolean insert(int data) {
        TreeNode node = new TreeNode(data);
        //局面1：新结点位于树根，没有父结点。
        if (root == null) {
            root = node;
            node.color = BLACK;
            return true;
        }
        TreeNode targetNode = root;
        while (targetNode != null) {
            if( data == targetNode.data){
                System.out.println("红黑树中已有重复的结点：" + data);
                return false;
            } else if (data > targetNode.data) {
                if(targetNode.right == null){
                    targetNode.right = node;
                    node.parent = targetNode;
                    insertAdjust(node);
                    return true;
                }
                targetNode = targetNode.right;
            } else {
                if(targetNode.left == null){
                    targetNode.left = node;
                    node.parent = targetNode;
                    insertAdjust(node);
                    return true;
                }
                targetNode = targetNode.left;
            }
        }
        return true;
    }

    //插入后自我调整
    private void insertAdjust(TreeNode node) {
        //创建父结点和祖父结点指针
        TreeNode parent, grandParent;
        //局面3的调整有可能引发后续的一系列调整，所以使用while循环。
        while (node.parent != null && node.parent.color == RED) {
            parent = node.parent;
            grandParent = parent.parent;
            if (grandParent.left == parent) {
                TreeNode uncle = grandParent.right;
                //局面3：新结点的父结点和叔叔结点都是红色。
                if (uncle != null && uncle.color == RED) {
                    parent.color = BLACK;
                    uncle.color = BLACK;
                    grandParent.color = RED;
                    node = grandParent;
                    continue;
                }
                //局面4：新结点的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的右孩子，父结点是祖父结点的左孩子。
                if (node == parent.right) {
                    leftRotate(parent);
                    TreeNode tmp = node;
                    node = parent;
                    parent = tmp;
                }
                //局面5：新结点的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的左孩子，父结点是祖父结点的左孩子。
                parent.color = BLACK;
                grandParent.color = RED;
                rightRotate(grandParent);
            } else {
                TreeNode uncle = grandParent.left;
                //局面3（镜像）：新结点的父结点和叔叔结点都是红色。
                if (uncle != null && uncle.color == RED) {
                    parent.color = BLACK;
                    uncle.color = BLACK;
                    grandParent.color = RED;
                    node = grandParent;
                    continue;
                }
                //局面4（镜像）：新结点的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的左孩子，父结点是祖父结点的右孩子。
                if (node == parent.left) {
                    rightRotate(parent);
                    TreeNode tmp = node;
                    node = parent;
                    parent = tmp;
                }
                //局面5（镜像）：新结点的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的右孩子，父结点是祖父结点的右孩子。
                parent.color = BLACK;
                grandParent.color = RED;
                leftRotate(grandParent);
            }
        }
        //经过局面3的调整，有可能把根结点变为红色，此时再变回黑色即可。
        if(root.color == RED){
            root.color = BLACK;
        }
    }

    //删除节点
    public void remove(int key) {
        remove(search(key));
    }

    //删除节点详细逻辑
    private void remove(TreeNode node) {
        TreeNode targetNode = node;
        if (node == null)
            return;
        //第一步：如果待删除结点有两个非空的孩子结点，转化成待删除结点只有一个孩子（或没有孩子）的情况。
        if (node.left != null && node.right != null) {
            //待删除结点的后继结点
            TreeNode successNode = targetNode.right;
            while(successNode.left != null) {
                successNode = successNode.left;
            }
            if(targetNode == root) {
                root = successNode;
            }
            //把后继结点复制到待删除结点位置
            targetNode.data = successNode.data;
            remove(successNode);
            return;
        }
        //第二步：根据待删除结点和其唯一子结点的颜色，分情况处理。
        TreeNode successNode = node.right; //node只可能拥有右孩子或没有孩子
        TreeNode parent = node.parent;
        if (parent == null) {
            //子情况1，被删除结点是红黑树的根结点：
            root = successNode;
            if (successNode != null)
                successNode.parent = null;
        } else {
            //无论何种情况，都需要先删除node结点
            if (successNode != null)
                successNode.parent = parent;
            if (parent.left == node)
                parent.left = successNode;
            else {
                parent.right = successNode;
            }
        }
        //此时情况1已处理完毕，如果父结点是黑色结点，则增加额外处理
        if (node.color == BLACK)
            if(successNode!=null && successNode.color == RED ){
                //情况2：父结点是黑，子节点是红
                successNode.color = BLACK;
            }else {
                //情况3：遇到双黑结点。此时进入第三步，在子结点顶替父结点之后，分成6种子情况处理。
                removeAdjust(parent, successNode);
            }
    }

    //删除结点后的自我调整
    private void removeAdjust(TreeNode parent, TreeNode node) {
        while ((node == null || node.color == BLACK) && node != root) {
            if (parent.left == node) {
                //node的兄弟节点
                TreeNode sibling = parent.right;
                //子情况3，node的兄弟结点是红色：
                if (sibling != null && sibling.color == RED) {
                    parent.color = RED;
                    sibling.color = BLACK;
                    leftRotate(parent);
                    sibling = parent.right;
                }
                if (sibling == null || ((sibling.left == null || sibling.left.color == BLACK) && (sibling.right == null || sibling.right.color == BLACK))) {
                    //子情况2（镜像），node的父结点是黑色，兄弟和侄子结点是黑色：
                    if(parent.color == BLACK){
                        sibling.color = RED;
                        node = parent;
                        parent = node.parent;
                        continue;
                    }
                    //子情况4（镜像），node的父结点是红色，兄弟和侄子结点是黑色：
                    else {
                        sibling.color = RED;
                        break;
                    }
                }
                //子情况5，node的父结点随意，兄弟结点是黑色右孩子，左侄子结点是红色：
                if (sibling.color == BLACK && sibling.left!=null && sibling.left.color == RED) {
                    rightRotate(sibling);
                    sibling.parent.color = BLACK;
                    sibling.color = RED;
                    sibling = sibling.parent;
                }
                //子情况6，node的父结点随意，兄弟结点是黑色右孩子，右侄子结点是红色：
                if (sibling.color == BLACK && sibling.right!=null && sibling.right.color == RED) {
                    leftRotate(sibling.parent);
                    sibling.color = sibling.left.color;
                    sibling.left.color = BLACK;
                    sibling.right.color = BLACK;
                }
                node = root; //跳出循环
            } else {
                //node的兄弟节点
                TreeNode sibling = parent.left;
                //子情况3（镜像），node的兄弟结点是红色：
                if (sibling != null && sibling.color == RED) {
                    parent.color = RED;
                    sibling.color = BLACK;
                    rightRotate(parent);
                    sibling = parent.left;
                }
                if (sibling == null || ((sibling.left == null || sibling.left.color == BLACK) && (sibling.right == null || sibling.right.color == BLACK))) {
                    //子情况2（镜像），node的父结点是黑色，兄弟和侄子结点是黑色：
                    if(parent.color == BLACK){
                        sibling.color = RED;
                        node = parent;
                        parent = node.parent;
                        continue;
                    }
                    //子情况4（镜像），node的父结点是红色，兄弟和侄子结点是黑色：
                    else {
                        sibling.color = RED;
                        break;
                    }
                }
                //子情况5（镜像），node的父结点随意，兄弟结点是黑色左孩子，右侄子结点是红色：
                if (sibling.color == BLACK && sibling.right!=null && sibling.right.color == RED) {
                    leftRotate(sibling);
                    sibling.parent.color = BLACK;
                    sibling.color = RED;
                    sibling = sibling.parent;
                }
                //子情况6（镜像），node的父结点随意，兄弟结点是黑色左孩子，左侄子结点是红色：
                if (sibling.color == BLACK && sibling.left!=null && sibling.left.color == RED) {
                    rightRotate(sibling.parent);
                    sibling.color = sibling.right.color;
                    sibling.right.color = BLACK;
                    sibling.left.color = BLACK;
                }
                node = root; //跳出循环
            }
        }
        if (node != null) {
            node.color = BLACK;
        }
    }

    //左旋转
    private void leftRotate(TreeNode node) {
        TreeNode right = node.right;
        TreeNode parent = node.parent;
        if (parent == null) {
            root = right;
            right.parent = null;
        } else {
            if (parent.left != null && parent.left == node) {
                parent.left = right;
            } else {
                parent.right = right;
            }
            right.parent = parent;
        }
        node.parent = right;
        node.right = right.left;
        if (right.left != null) {
            right.left.parent = node;
        }
        right.left = node;
    }

    //右旋转
    private void rightRotate(TreeNode node) {
        TreeNode left = node.left;
        TreeNode parent = node.parent;
        if (parent == null) {
            root = left;
            left.parent = null;
        } else {
            if (parent.left != null && parent.left == node) {
                parent.left = left;
            } else {
                parent.right = left;
            }
            left.parent = parent;
        }
        node.parent = left;
        node.left = left.right;
        if (left.right != null) {
            left.right.parent = node;
        }
        left.right = node;
    }

    //中序遍历
    public static void inOrderTraversal(TreeNode node) {
        if(node != null) {
            inOrderTraversal(node.left);
            System.out.print(node);
            inOrderTraversal(node.right);
        }
    }

    //层序遍历
    public static void levelOrderTraversal(TreeNode root){
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            TreeNode node = queue.poll();
            System.out.print(node);
            if(node.left != null){
                queue.offer(node.left);
            }
            if(node.right != null){
                queue.offer(node.right);
            }
        }
    }

    class TreeNode {
        int data;
        boolean color;
        TreeNode left;
        TreeNode right;
        TreeNode parent;

        public TreeNode(int data) {
            this.data = data;
            this.color = RED;
        }

        @Override
        public String toString() {
            return  data + (color?"(red)":"(black)") + "  " ;
        }
    }

    public static void main(String[] args) {
        //case 1:
        RedBlackTree rbTree = new RedBlackTree();
        int input[]= {13,8,17,1,11,15,25,6,22,27};
        for(int i=0; i<10; i++) {
            rbTree.insert(input[i]);
        }
        rbTree.remove(25);
        System.out.println("中序遍历: ");
        inOrderTraversal(rbTree.root);
        System.out.println();
        System.out.println("层序遍历: ");
        levelOrderTraversal(rbTree.root);
        System.out.println();

        //case 2:
        rbTree = new RedBlackTree();
        for(int i=0; i<1000; i++) {
            rbTree.insert(i);
        }
        for(int i=100; i<1000; i+=100) {
            rbTree.remove(i);
        }
        System.out.println("中序遍历: ");
        inOrderTraversal(rbTree.root);
        System.out.println();
        System.out.println("层序遍历: ");
        levelOrderTraversal(rbTree.root);
        System.out.println();

    }
}