前言:
上一章,对交换排序的冒牌和快排做了复盘,这一章对,归并排序以及非比较排序中的计数排序做一个复盘。
目录
2.4归并排序
2.4.1规定递归
2.4.2归并非递归
2.5非比较排序
2.5.1计数排序
2.6排序的稳定性分析
2.6.1冒泡排序
2.6.2 简单选择排序
2.6.3 直接插入排序
2.6.4希尔排序
2.6.5堆排序
2.6.6归并排序
2.6.7快速排序
2.4归并排序
2.4.1规定递归
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。动态图如下所示:

图解如下:
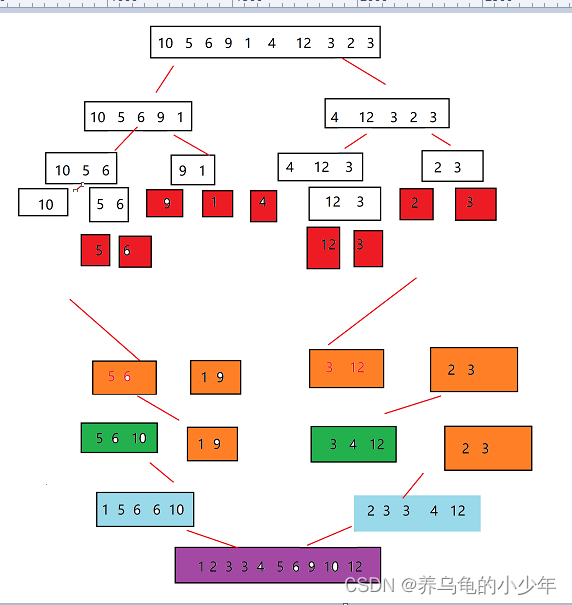
红色的方块,代表已经分治到最后一层,要开始归并,归并如果在原数组上进行,会出现数值被覆盖的情况,所以需要重新开辟一个等大小的数组代码如下:
// 开辟拷贝数组
int* temp = malloc(sizeof(int) * n );
if (temp == NULL)
{
perror("malloc");
exit(-1);
}归并思想,就是比价两个元素的大小,按顺序放置进数组,然后将新数组拷贝回原数组,代码如下:
//开始归并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;//为了记住需要拷贝到temp数组的位置 要和原数组一一对应。
while (begin1<=end1 && begin2<=end2)
{
if (a[begin1] < a[begin2]) //判断清楚 是下标还是数值 弟弟
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end)
{
temp[i++] = a[begin2++];
}
memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));//拷贝回原数组return 上一级递归 再次归并
}归并排序也是利用递归的思想,这一层比较完后,返回上一层,继续完成相同的操作,但是,由于开辟了新数组,所以我们将递归在子函数中完成,具体代码如下:
void _MergeSort(int* a, int begin, int end, int* temp)
{
//结束递归条件
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
_MergeSort(a, begin, mid, temp);
_MergeSort(a, mid+1, end,temp);
//归并
}
复杂度分析:
归并排序采用的也是分治的思想,二分比较,所以时间复杂度也为O(n*logn)
快排和归并以及堆时间复杂度都是一个量级的到底他们谁更优越呢,我们可以通过一个程序,来进行比较看看他们从开始运行到结束,花费了多长时间,具体代码如下:
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
int begin1 = clock();
//InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
//ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
//SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort1(a1, 0, N - 1);
int end5 = clock();
int begin6 = clock();
//MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
//BubbleSort(a7, N);
int end7 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("BubbleSort:%d\n", end7 - begin7);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
}为了方便观察,我先屏蔽其他不相关,只保留需要比较的三个,最好将终端调制release版下,运行结果如下 :
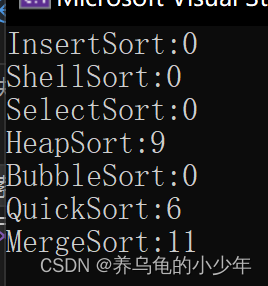
还是快排更快一点,怪不得它叫快排。
2.4.2归并非递归
归并递归排序思想是 分治后层层递归,很像斐波那契,F(N) = F(N - 1) + F(N - 2) 求 F(N) 只要求得 F(N - 1 ) 和 F(N - 2) 一层层 递归到 F(1) 。如果我们不用递归,逆过来用F(1) + F(2) + ....F(N - 1) 同样可以得到F(N )
同样归并非递归,我们也可以逆过来,一个个归并,两个两个归并,四四归并最后归并成有序数组,但是这是有问题的如果数组元素个数是奇数的话,会出现越界情况,如下代码:
void MergeNorSort(int* a, int n)
{
// 开辟拷贝数组
int* temp = malloc(sizeof(int) * n);
if (temp == NULL)
{
perror("malloc");
exit(-1);
}
//步长 比较距离
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i,end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
printf("[%d %d],[%d,%d]", begin1, end1, begin2, end2);
//归并
int j = i;
//if (end1 >= n || begin2 >= n)
//{
// break;
//}
//if (end2 >= n)
//{
// end2 = n - 1;
//}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2]) //判断清楚 是下标还是数值 弟弟
{
temp[j++] = a[begin1++];
}
else
{
temp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[j++] = a[begin2++];
}
memcpy(a + i, temp + i, sizeof(int) * (end2 - i + 1));
}
printf("\n");
gap *= 2;
}
free(temp);运行结果如下:
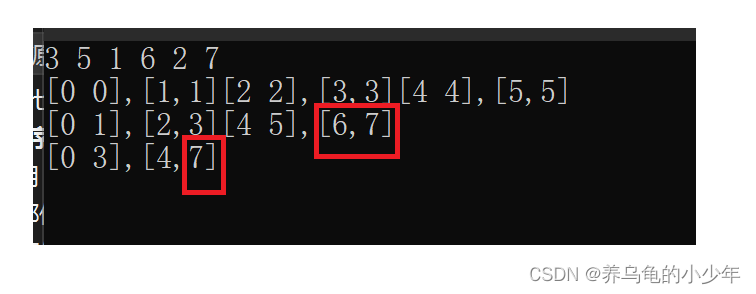
会出现,归并的边界下标出现越界的情况,如何对其进行改进呢,这时候需要分类分析:
如果是 begin2或者end1越界了,那这层就不用归并了,直接跳出本次归并的循环,如果,只是end2越界了的话,我们可以修改,下标,让其为n - 1,继续归并,图解如下所示:
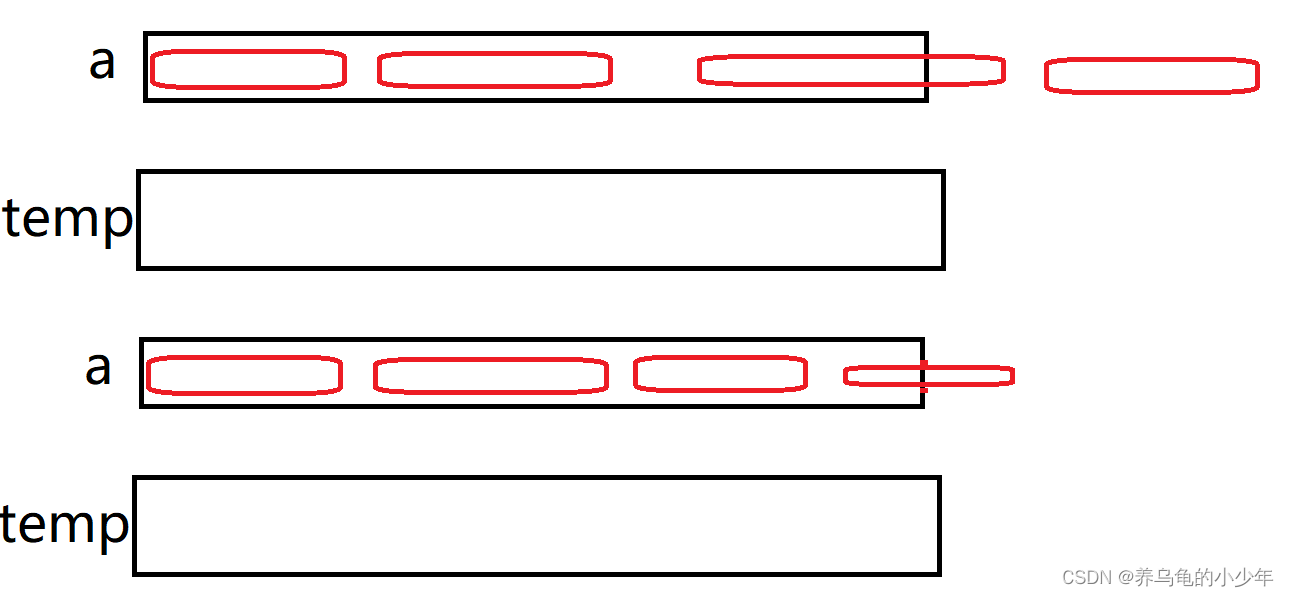
代码优化如下:
if (end1 >= n || begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}运行结果如下:
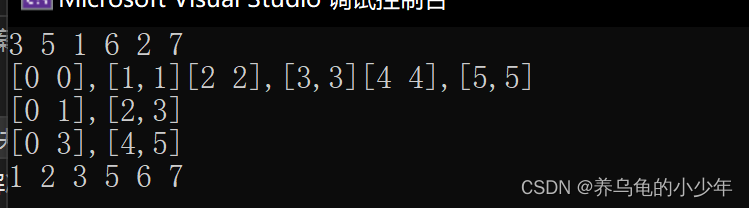
2.5非比较排序
非比较排序有很多,基数排序,计数排序,桶排序,等 我主要复盘一下,计数排序
2.5.1计数排序
计数排序,是利用计数原理,对需要排序的数组,进行遍历计数,统计次数后,相对映射到新开辟的数组,然后排序,图解如下:

代码如下:
//计数排序
void CountSort(int* a, int n)
{
//选出最大数和最小数
int max = a[0], min = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] <= min)
{
min = a[i];
}
if (a[i] >= max)
{
max = a[i];
}
}
//相对大小
int range = max - min + 1;
//重新开辟一个数组 用来记录 不同元素出现的个数
int* countA = (int *)calloc(range,sizeof(int));
if (countA == NULL)
{
perror("calloc:fail");
exit(-1);
}
//将 数组a中元素通过相对位置 计算出重复个数
for (int i = 0; i < n; i++)
{
countA[a[i] - min]++;
}
int j = 0;
for (int i = 0; i < range; i++)
{
while (countA[i]--)
{
a[j++] = i + min;
}
}
free(countA);
}总结:计数排序适合范围比较集中,且范围不大的整形数组,不适合范围比较分散,且范围很大的非整形数,例如 浮点数,字符串。
2.6排序的稳定性分析
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的,例如:一个数组中 出现前后两个相同的数,排序完成后,前后相同的元素位置不变。如下图所示:
2.6.1冒泡排序
稳定性:很稳,相同的元素不会发生交换。
2.6.2 简单选择排序
稳定性:不稳定,寻找到需要的元素 可能不会影响到本身元素的稳定性,但是会影响到别的元素的位置。如下图所示:
2.6.3 直接插入排序
稳定性:很稳定
2.6.4希尔排序
稳定性:不稳定,相同元素会在预排序的过程分到不同组中,导致,相同元素的前后位置发生变化。
2.6.5堆排序
稳定性:不稳定,交换根和最后一个元素 就可能会影响元素位置变化,如下如所示:
2.6.6归并排序
稳定性:很稳,只要在程序中将begin1和begin2相等的时候,归并begin1就可以了。
2.6.7快速排序
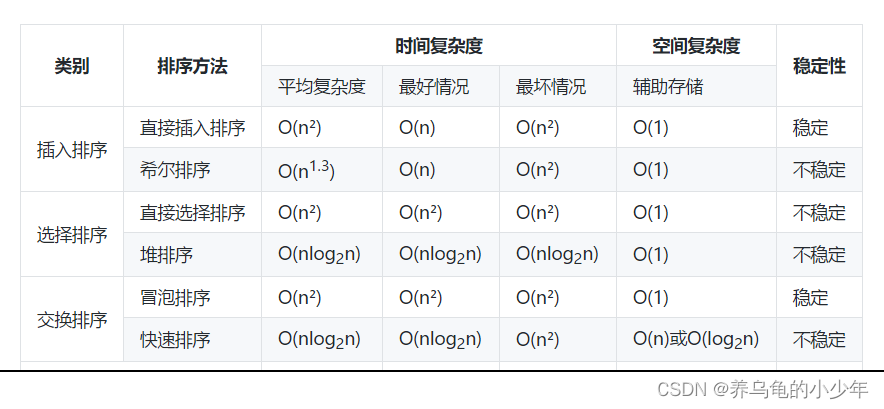
稳定性:不稳定,
总结成一个表格如下所示: