导读

通过使用生物物理模型来解释弛豫-扩散MRI大脑数据，可以研究白质微观结构的具体特征。尽管更复杂的模型有可能揭示组织的更多细节，但也会导致参数估计耗时较长，由于简并拟合地形中普遍存在局部最小值，这些参数估计可能会收敛到不准确的解。已提出机器学习拟合算法来加速参数估计并提高估计结果的鲁棒性。到目前为止，基于学习的拟合方法仅限于独立模型参数数量较少的微结构模型，这些模型易于生成密集的训练数据集。此外，机器学习在多大程度上可以缓解简并问题还知之甚少。对于传统的最小二乘求解器，已经证明可以通过使用优化的弛豫-扩散相关协议(包括张量值扩散编码)进行采集来避免简并。机器学习技术是否能够补偿这些采集需求仍有待测试。本文采用人工神经网络极大地加速了白质微结构弛豫-扩散模型的参数估计。本研究还制定了评估功能拟合网络准确性和敏感性的策略，并使用这些策略来探索采集协议的影响。利用最优和次优采集协议获取的弛豫-扩散数据对开发的基于学习的拟合管道进行测试。观察到使用优化协议训练的网络可以在短计算时间内提供准确的参数估计。比较神经网络和最小二乘求解器可以发现，前者的性能受次优协议的影响较小；然而，模型拟合网络仍然容易受到简并问题的影响，并且它们的使用不能完全取代精心设计的采集协议。

前言

微结构成像使用扩散MRI(dMRI)数据的隔室模型，旨在绘制特定的组织数量。微结构成像的一个中心目标是估计不同微结构成分（如轴突）的体积分数。然而，估算体积分数而不是信号分数是具有挑战性的，因为它需要同时估算不同模型隔室的扩散和弛豫特性。这类逆问题对简并性问题敏感，其中多组模型参数同样能很好地描述所获取的数据。参数估计的计算速度也可能很慢，从而不利于实时映射。一个潜在的解决方案是使用机器学习来加速参数估计过程。然而，目前的文献缺乏对这种方法的优点和缺点的系统评估。

人工神经网络(ANN)和其他机器学习方法已被应用于加速dMRI数据的微观结构参数估计。例如，随机森林回归器已用于拟合存在水交换时白质(WM)微观结构的隔室模型，以及拟合灰质特性的SANDI模型。Reisert等人(2017)将机器学习应用于贝叶斯估计方法，这极大地加快了二室和三室模型的拟合。

Barbieri等人(2020)将ANN应用于体素内不相干运动模型。然而，一个重要的开放性问题是，训练策略对拟合性能有什么影响。当应用于具有许多独立模型参数的非线性多隔室模型时，这一点尤其重要，本文在这里将其大致称为“高维模型”。训练数据的生成随模型参数数量的增加而伸缩性较差，因为在m步中对p个模型参数的每个组合进行采样需要mp个样本。随着p的增大，有限样本集在p维模型参数空间中变得稀疏是不可避免的，存在选择偏倚的风险。在这里，本文研究了该空间中不同采样模式对神经网络性能的影响。

除了加速模型拟合之外，神经网络原则上还可以通过从训练示例中学习先验来降低对成像协议的要求。例如，神经网络已被用于学习全采样和子采样数据集之间的映射，这反过来又可用于在大量数据下采样的情况下稳定模型拟合性能。然而，我们并不期望机器学习方法能够完全缓解简并问题。事实上，对于采集协议没有提供足够信息来解析不同参数值的情况，基于学习的估计将简单地等于用于训练模型参数分布的平均值。

本研究的目的是比较训练策略，提出评估模型拟合神经网络性能的工具，并测试神经网络可以在多大程度上解决简并问题。本研究采用WM的高维弛豫-扩散微观结构模型。对于这个模型，参数估计是通过最先进的成像协议实现的，该协议具有所谓的b张量编码与扩散-弛豫相关性相结合。本文研究了神经网络加速模型拟合的能力，并探索了它们在多大程度上可以补偿采集协议的要求。

理论

 

 

 

方法

神经网络架构和训练

本研究在MATLAB R2020b(The MathWorks，Inc.)中构建了前馈神经网络，并使用它们来拟合标量参数向量m=(fS,DI;S,DI;Z,DΔ;Z,T2;S,T2;Z,p20,Re(p21),Im(p21),Re(p22),Im(p22))，到测量集S(τE，B)。在决定两个最终网络架构之前，本研究探索了具有不同数量隐藏节点或层的各种网络设计：一个是具有3个全连接隐藏层的人工神经网络，但节点数量递减(180、80和55)，另一个是具有4个全连接隐藏层的更深/更宽的神经网络，每个隐藏层有250个节点。所有隐藏层均由双曲正切(tanh)函数激活，更深/更宽的网络在全连接的内层及其各自的tanh激活之间也具有批量归一化层。为了区分这些网络，本研究将它们分别称为浅层神经网络(SNN)和深层神经网络(DNN)。SNN和DNN都包含一个输出层，有11个节点，对应于m中的参数。输入由给定数量(E)的信号样本组成，通过预定义的弛豫-扩散编码协议获取。本研究考虑了三种不同的采集协议；E=164、E=242和E=270个样本(τE，B)。对每个协议进行独立网络训练，即评估了3个SNN和3个DNN。为了消除S0对拟合问题的影响，本研究将输入向量归一化为在最小b值和最短回波时间下获取的中值信号。

使用均方误差损失进行监督网络训练：

其中mtarg是地面真值目标向量，mnet是相应的网络输出向量，其中||·||2表示欧几里德范数。在提供给网络之前，使用最小-最大归一化策略在0和1之间重新调整mtarg参数。使用随机生成的模型参数和噪声信号样本S(τE，B)的体素集来训练网络。SNN用0.5·106的批量大小和缩放共轭梯度优化器进行训练。DNN以小批量方式进行训练，共使用5·106个训练集，小批量大小为50·103，并使用Adam优化器进行优化。在整个过程中，训练数据被划分为75%的原始数据用于更新权重和偏差，25%用于交叉验证。通过提前停止法解决过拟合问题，该方法在验证数据的MSE增加5(SNN)或20(DNN)个连续epoch后终止训练。

生成训练数据

本文研究了训练数据生成策略对网络性能的影响，包括基于均匀采样和真实大脑数据的训练。通过两种策略创建训练参数向量：

①munif是通过在表1中描述的范围内对不相关的均匀分布进行随机抽样而合成的；

②通过随机抽样由公式(10)的NLLS拟合估计的参数向量，从活体大脑数据中构建了mbrain。该数据集包含了在健康成年人的典型大脑数据集中发现的参数相关性。

表1.SMR参数范围。

mbrain向量包括公式(10)对体内信号数据的非线性最小二乘(NLLS)拟合的解，称为mfit，以及由拟合解的随机突变组成的附加参数集mmut，由下式给出：

训练向量mtrain是mbrain和munif参数向量的组合。使用给定的向量总数(ntot)和不同数量的mbrain参数(nbrain)，以0.05的步长在0和1之间调整体内大脑数据的分数，fbrain=nbrain/ntot。SNN训练集总共包含ntot=5·105个参数向量，而DNN训练集包含ntot=5·106个参数向量。

使用公式(10)和三种不同(τE，B)采集协议之一从mtrain生成信号数据。从Rice分布中采样噪声，并添加到地面真实合成信号中。因为弛豫-扩散MRI数据包括不同信噪比(SNR)的体素，所以S0＝S(τE=0，B=0)处SNR的幅值在SNR∈[80，160]区间内均匀变化。考虑到典型健康WM(T2≈70 ms，DI≈0.9μm2/ms)的弛豫-弥散特性，该选择在优化协议的最大信号点(τE=63ms，b=0.1ms/μm2)处的SNR∈[30，60]，SNR振幅与体内大脑张量值dMRI测量结果一致。最后，使用mtrain向量作为目标并将其对应的silico噪声信号作为输入来训练网络。

数据采集

本研究分析了Lampinen等人(2020)中报告的三名成年志愿者的数据。该研究获得了Lund地区伦理审查委员会的批准，扫描前所有志愿者均签署了书面知情同意书。在MAGNETOM Prisma 3T系统(Siemens Healthcare，Erlangen，Germany)上使用自旋回波EPI序列进行测量，该序列有助于用户定义扩散编码的梯度波形。数据采集的回波时间为63~130ms、重复时间为3.4s、体素大小为2.5mm3、40个时间层、矩阵大小为88×88、平面内加速度因子和平面间加速度因子为2×2(GRAPPA)、部分傅里叶为3/4、带宽=1775Hz/pixel，脂肪饱和度“强”。使用优化的梯度波形进行扩散编码，以最大化单位时间的编码强度，并抑制伴随的场效应。τE和B共有270种组合。总采集时间为15min。

体内数据处理与参数估计

在分析之前，使用ElastiX和推测目标体积对所有体内数据进行涡流伪影和运动伪影校正。使用FMRIB软件库(FSL)中的TOPUP工具对磁敏感引起的几何畸变进行校正。根据Kellner等人(2016)描述的方法进行Gibbs振铃伪影校正。为了抑制噪声的影响，本研究使用标准偏差为体素尺寸0.45倍的3D高斯核来过滤数据。

根据公式(10)对后处理数据进行逐体素NLLS拟合来估计SMR模型参数。使用多维dMRI工具箱(https://github.com/markus-nilsson/md-dmri)和MATLAB内置的lsqcurvefit函数进行拟合。为了去除异常值，对每个体素进行了两次模型拟合，并保留残差最小的结果。最后，使用先前训练好的网络从体内数据中估计公式(10)的参数。使用SNN和DNN分别大约需要2s和20s。在具有最佳fbrain分数的silico mbrain数据上进行训练。训练过程遵循“留一法”，对两个受试者生成的合成数据进行训练，然后在未经训练的第三个受试者上进行测试。神经网络拟合提供了体素参数图，并将其与传统NLLS拟合方法获得的参数图进行比较。

结果

神经网络参数估计

在同一台计算机上，基于SNN的参数估计比NLLS拟合的速度快约104倍，得到的参数与地面真实目标一致，并且保留了具有不同(T2，D)属性的区域之间的对比度(图1)。例如，估计的fS和p2通常在WM区域中较高，而在定向相干的WM区域(如胼胝体)中最高。然而，在T2;Z中观察到对比度降低，其中WM(较暗)和皮层GM(较亮)区域之间的区别在地面真值图中更为明显。T2;Z估计值还表现为在长T2区域(如侧脑室)中，地面真值和估计参数之间存在显著差异。估计值与地面真值之间的最大总体差异为DΔ;Z，可能是因为当|DΔ;Z|＜0.5时信号对其不敏感。使用在合成数据上训练的ANN直接拟合体内实验数据，得到了噪声更大的图。然而，它保留了一种解剖学上似乎合理的对比。考虑到silico地面真值图和网络估计之间的强相关性，体内参数图的噪声可能是因为SMR模型不能准确地表示潜在的活体数据。

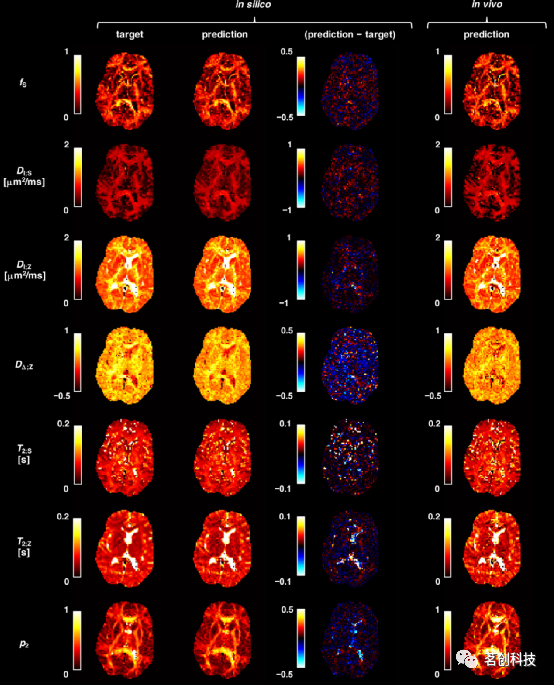
图1.将训练过的网络部署到未经训练的silico和活体数据上，可以在10s内提供解剖学上合理的参数图。

图2显示，基于SNN的估计与地面真值参数目标相关良好，大多数参数的线性相关系数接近或高于0.9。参考图着重于使用优化协议生成的silico S(τE，B)数据和均匀混合的随机类WM样本(fbrain=0.5)训练的网络性能，并区分了均匀随机采样获得的参数(浅蓝色点)和来自体内非皮质大脑数据的参数(深蓝色点)的性能。红点对应于从低分量特定信号分数导出的参数向量。当DΔ;Z值较小时，可以观察到性能较差，即无论地面真值如何，网络的输出DΔ;Z≈0.3。这可归因于在区分|DΔ;Z|＜0.5分量的扩散加权信号时存在的固有困难。此外，当T2;Z时间比最大回波时间长时，目标与估计的对应关系较差。

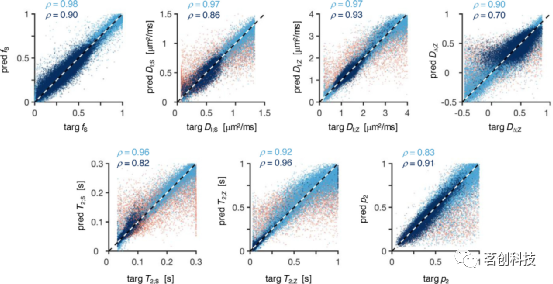
图2.地面真值参数与神经网络预测的散点图。

从深层网络估计的参数图与其各自的地面真值目标非常一致。基于DNN的拟合导致网络估计和地面真值参数目标之间的相关性略强。尽管DNN和SNN的体内图相似，但在DΔ;Z和T2;Z中可以发现差异。DNN产生DΔ;Z图噪声更大，而T2;Z图在WM和皮层GM之间具有更高的对比度。这表明DNN更容易受到SMR信号预测和体内测量数据之间差异的影响。

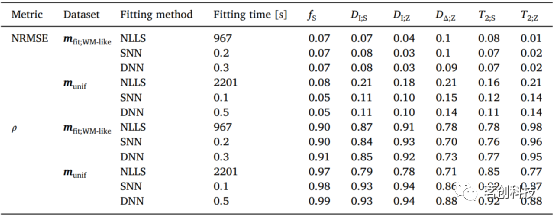
基于ANN估计的误差和预测-目标相关性汇总在表2中，其中还将它们与传统的NLLS求解器进行了比较。NLLS、SNN和DNN方法对于旨在捕获WM(T2，D)属性的silico数据集都具有相当的准确性。相比之下，对于合成的munif参数向量，函数拟合网络比NLLS方法更精确。

表2.基于DNN、SNN和NLLS拟合方法的精度。

采集协议对网络精度和灵敏度的影响

本节将重点讨论采集协议设计与网络性能之间的关系。图3显示，基于ANN的拟合可以部分但不能完全消除未优化和LTE-only协议中已知的拟合简并：基于优化协议的ANN比基于其他两种协议的ANN提供了更低的估计误差(NRMSE)。比较这两个协议可以发现，未优化协议对DI;S和T2;Z的估计相对更准确，而LTE-only协议对fS、DI;Z、DΔ;Z、T2;S和p2的估计更准确。图3还表明，与传统的NLLS方法相比，SNN和DNN的性能受次优采集协议的影响较小(图3)。对于NLLS方法，使用未优化或LTE-only协议会导致估计误差显著增加，而对于DNN或SNN方法，仅观察到NRMSE略有增加。这表明ANNs可以在一定程度上缓解由与微观结构模型相关的协议不充分而导致的参数估计困难。

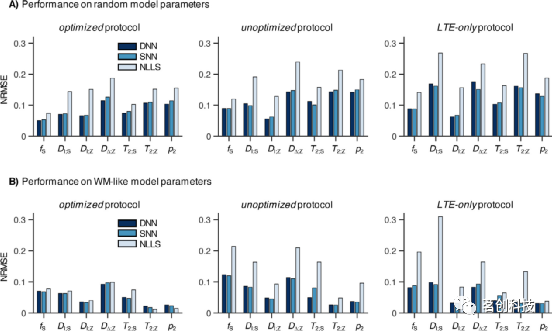
图3.优化的采集协议使得基于ANN和NLLS的参数估计误差更小。

图4显示了各种协议对参数变化的敏感性。使用优化协议生成的数据进行训练的网络对所有参数都很敏感，但略微低估了变化的幅度，特别是在DΔ;Z中。特定参数调制对其余未调制参数的估计没有重大影响。但当T2;Z增加10%时的情况除外，这导致未变化的DI;S被高估了3%。与优化协议相比，未优化和LTE-only协议对小参数调制的敏感性较低，并且似乎对DΔ;Z(两种协议)和DI;S(LTE-only)的变化无响应。除了较低的灵敏度外，未优化协议还导致对未调制参数的估计不准确，10%的fS调制会导致T2;S错误增加7%。

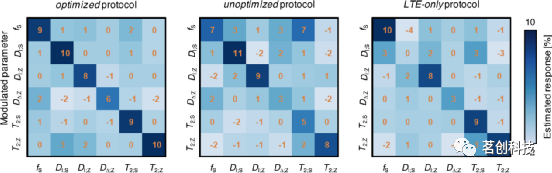
图4.采集协议对10%参数调制的灵敏度。

旋转不变性微观结构特征的神经网络拟合

图5A显示，使用旋转不变量训练SNN会导致目标参数和估计参数之间的相关性略强(与图2的散点图相比)。当DΔ;Z值较小时，精度有了相当大的提高，此时完整SMR模型(见图2)中观察到的常量DΔ;Z≈0.3行为不再存在。将旋转不变性(RotInv)网络应用于看不见的体内Sl={0,2}数据集会产生具有解剖学合理对比的参数图(见图5B)。可以看到，RotInv DΔ;Z图具有更平滑的外观，并且比其非旋转不变SMR对应图更好地界定了皮质/非皮质实质(将图1的第四列与图5B进行比较)。

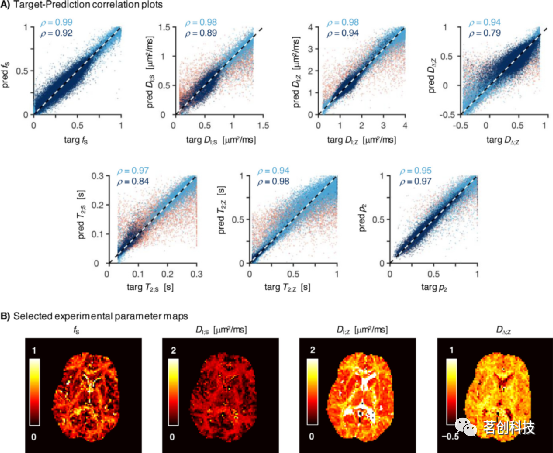
图5.旋转不变(RotInv)模型的神经网络拟合产生了强目标估计相关性和合理的映射。

有趣的是，在不合理噪声的silico数据上训练的ANN可以获得比图5B中更平滑的体内地形图。图6显示了在S0处使用SNR∈[20,40]训练的RotInv网络获得的体内参数图，比图5的SNR低4倍。与相对更嘈杂的图5B相比，虽然人们倾向于选择图6中诱人的“稳健”地形图，但可以注意到低SNR RotInv网络导致目标参数和估计参数之间的相关性较弱(将图6的散点图与图5的散点图进行比较)。例如，基于SNN的DΔ;Z估计可能会产生一个看似稳健的平滑图，但仔细检查会发现WM和深度GM区域中的DΔ;Z估计等于目标DΔ;Z分布的平均值，并导致对地面真值的估计极其不准确。

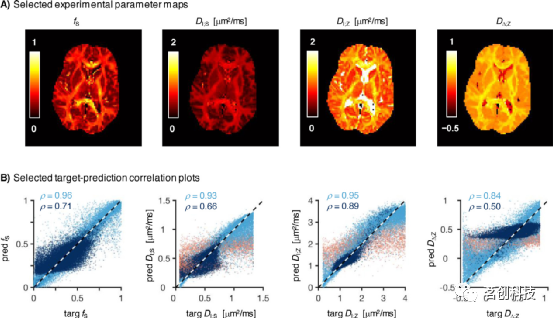
图6.在数据集不足的情况下训练神经网络可能会产生看似合理的地图，但目标估计相关性较差。

结论

函数拟合神经网络可用于极大地加速高维微结构MRI模型的参数估计。与传统的NLLS拟合相比，基于ANN估计的准确性受次优协议的影响较小。然而，函数拟合网络的性能仍然主要取决于基础测量所采样的信息量，并且没有发现证据表明基于ANN的方法可以补偿对丰富数据集的需求。因此，MRI微结构建模中的机器学习方法应与全面的数据采集相匹配。本研究提出了一种基于学习的拟合框架，以及用于在误差度量、估计-目标相关图和灵敏度矩阵方面评估网络和测量协议组合的工具。

原文：Neural networks for parameter estimation in microstructural MRI: Application to a diffusion-relaxation model of white matter.