许多测量涉及多个传感器异步采集的数据。如果您要集成信号并以关联式研究它们,您必须同步它们。为此,请使用 xcorr。
例如,假设有一辆汽车经过一座桥。它产生的振动由位于不同位置的三个相同传感器进行测量。信号有不同到达时间。
- 将三个时间轴并未同步的信号plot出来
ax(1) = subplot(3,1,1);
plot(s1)
ylabel('s_1')
axis tight
ax(2) = subplot(3,1,2);
plot(s2)
ylabel('s_2')
axis tight
ax(3) = subplot(3,1,3);
plot(s3)
ylabel('s_3')
axis tight
xlabel('Samples')
linkaxes(ax,'x')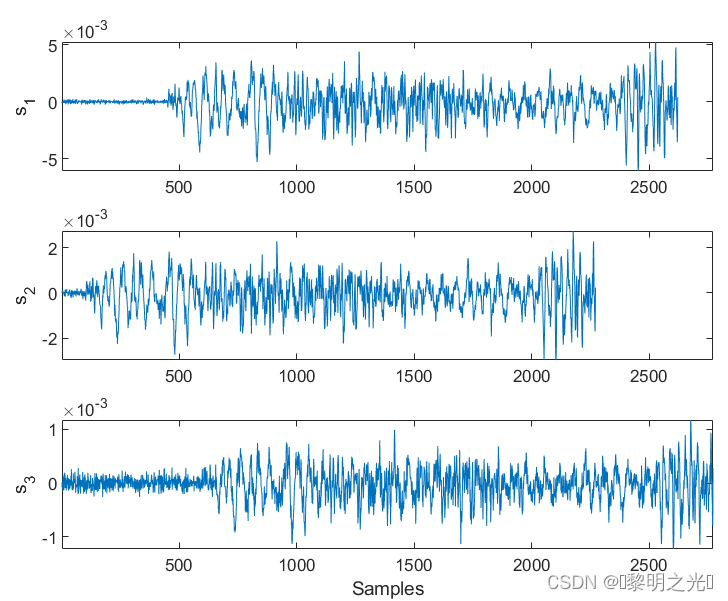
可以发现三个信号包络相同,但时延不同。即同一时间点信号有先有后。
- 计算三对信号之间的互相关性
将它们归一化,使其最大值为 1
[C21,lag21] = xcorr(s2,s1);
C21 = C21/max(C21);
[C31,lag31] = xcorr(s3,s1);
C31 = C31/max(C31);
[C32,lag32] = xcorr(s3,s2);
C32 = C32/max(C32);xcorr是MATLAB中的一个函数,用于计算两个序列之间的互相关或自相关。xcorr函数的语法如下:[C,lag] = xcorr(A,B),其中A和B是两个输入序列,C是它们之间的互相关或自相关,lag是延迟向量。在我提供的代码中,s1和s2是两个输入序列,xcorr(s2,s1)计算了s2和s1之间的互相关,并返回结果C和lag。其余同理
互相关性最大值的位置指示领先或滞后时间
[M21,I21] = max(C21);
t21 = lag21(I21);
[M31,I31] = max(C31);
t31 = lag31(I31);
[M32,I32] = max(C32);
t32 = lag31(I32);在我提供的代码中,M21是C21中的最大值,I21是C21中最大值的索引,t21是lag21中与C21中最大值对应的延迟。
- 绘制互相关图。
在每个绘图中显示最大值的位置。
subplot(3,1,1)
plot(lag21,C21,[t21 t21],[-0.5 1],'r:')
text(t21+100,0.5,['Lag: ' int2str(t21)])
ylabel('C_{21}')
axis tight
title('Cross-Correlations')
subplot(3,1,2)
plot(lag31,C31,[t31 t31],[-0.5 1],'r:')
text(t31+100,0.5,['Lag: ' int2str(t31)])
ylabel('C_{31}')
axis tight
subplot(3,1,3)
plot(lag32,C32,[t32 t32],[-0.5 1],'r:')
text(t32+100,0.5,['Lag: ' int2str(t32)])
ylabel('C_{32}')
axis tight
xlabel('Samples')plot(lag21,C21,[t21 t21],[-0.5 1],‘r:’)将绘制一个由向量lag21和C21定义的线条,并在x轴上标记为t21。此外,它还将在x轴上标记一条红色垂直线,该线与y轴交叉点为-0.5和1,横坐标为t21。
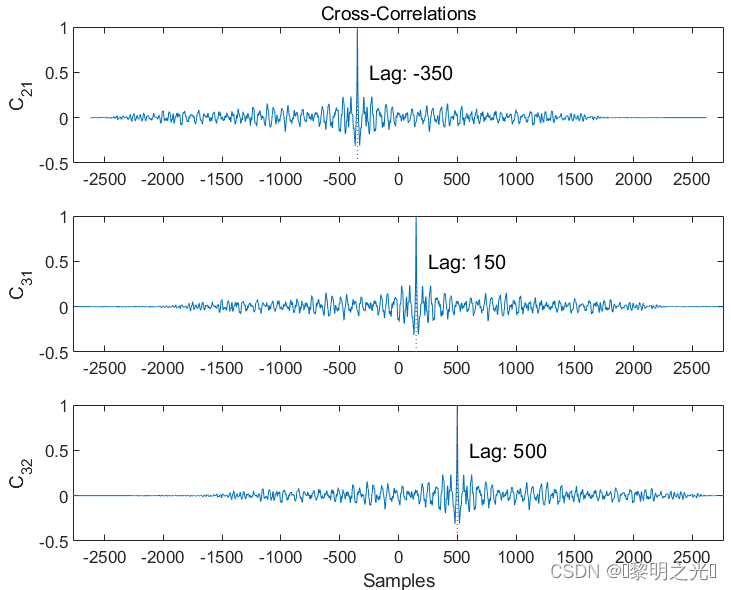
由上图可知,s2 领先于 s1 350 个样本;s3 落后于 s1 150 个样本。因此,s2 领先于 s3 500 个样本。通过截断具有较长延迟的向量来对齐信号。
- 信号截断
s1 = s1(-t21:end);
s3 = s3(t32:end);
ax(1) = subplot(3,1,1);
plot(s1)
ylabel('s_1')
axis tight
ax(2) = subplot(3,1,2);
plot(s2)
ylabel('s_2')
axis tight
ax(3) = subplot(3,1,3);
plot(s3)
ylabel('s_3')
axis tight
xlabel('Samples')
linkaxes(ax,'x')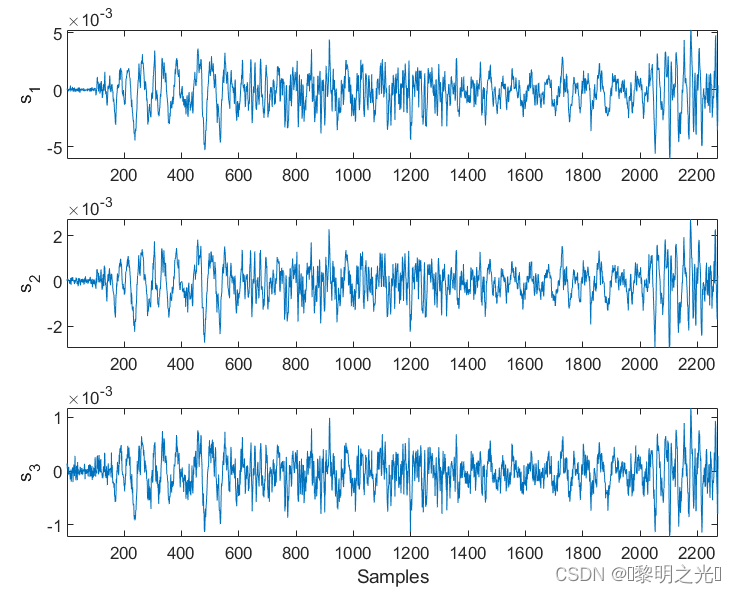
这些信号现在已同步,可用于进一步处理。