一文！解决恒定磁场的基本方程（有介质）

news2024/9/25 3:24:35

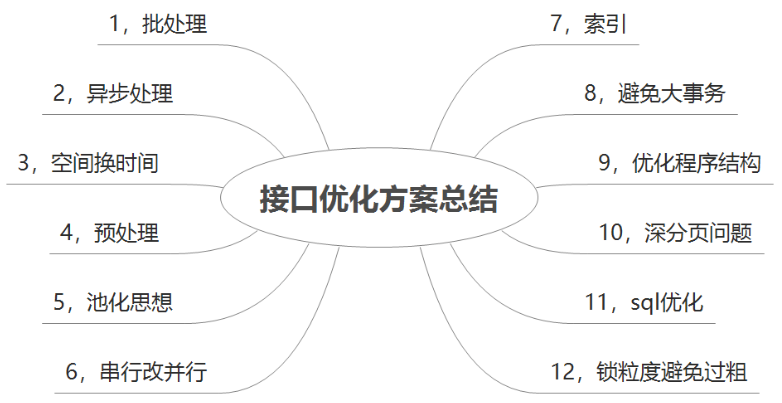
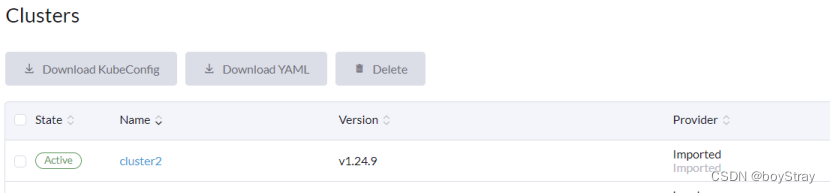
目录

引言

磁化过程

磁偶极矩

磁化强度

方程的化简

磁场强度

磁化率 磁导率 相对磁导率

现实生活中的应用

引言

为什么介质在磁场中会被磁化呢?

首先因为电子绕着原子核转动，所以就可以形成一个环形电流，，环形电流就可以产生磁场。因为在原先情况中环形电流是无规则分布的，所以站在统计学角度上看，所有环形电流的磁效应都被抵消掉了，所以对外不显示磁效应。现在因为外界施加磁场，所以每一个环形电流都会按照一定取向去排布，从而对外产生磁效应。

磁化过程

如同在电场中，我们把电偶极子看作是一个基本单位，在磁场中我们的基本单位就是磁偶极子

磁偶极子就是一个环形电流

磁偶极矩

我们定义磁偶极矩

\vec m=I \vec S

其中S的方向与电流的环流方向符合右手法则，而环流线圈的大小则由S的大小所决定

所以在外磁场的作用下，每一个环流线圈都想要让通过自己的磁通量最大，所以会呈一定的规则分布

那么在此时介质内部就会出现无数磁场线，宏观上就会产生磁效应

因为环形电流也按照一定的排列，所以在宏观上也就会产生电流（这个电流称之为磁化电流）

其实从另一个角度也不难理解

因为磁场是由一个又一个环路组成，而环形电流又是和磁环相互嵌套的，所以在出现磁场线的时候，必然相伴而生的会有环形电流的存在

因为电流是磁场的因，所以我们想办法把磁化电流进行等效，我们按照有介质的高斯定理的处理思路，我们可以把磁化电流等效成体电流还有面电流

磁化强度

我们定义一个新的物理量，磁化强度（此处可以类比极化强度）

就是将单位体积内的所有磁偶极矩求和，并取极限，这样我们就得到了等效的磁偶极矩

\vec M=lim_{\Delta v->0}\frac{\sum \vec m_i}{\Delta v}

\vec J_m=\nabla \times \vec M

\vec K_m = \vec M \times \vec e_n

 大家可以想一下，磁化强度就是在该点等效的磁偶极矩，也就可以写作

\vec M_{equal}=I_{equal} \ \vec S_{small},我们现在已知了\vec M_{equal}，如何求I呢

我们只需要对它求旋度，就可以把后面的环向量给约掉

所以\vec J_m=\nabla \times \vec M

而关于面磁化电流的理解可以看这一段

所以此时我们可以把整个介质撤走，换成我们等效出的面磁化电流和体磁化电流 

方程的化简

引入了之后我们还需要对方程进行一些化简 

因为磁化电流和自由电流的效果等效，所以安培环路定律就要变成

\oint_{L}\vec B \cdot d \vec l=\mu_0(I+I_{m})

而I_m=\oint_{S}J_m\cdot d\vec S

方程变为

\oint_{L}\vec B \cdot d \vec l=\mu_0( I + \oint_{S}J_m\cdot d\vec S )=\mu_0( I + \oint_{S}(\nabla \times \vec M) \cdot d\vec S )=\mu_0( I + \oint_{L} \vec M \cdot d\vec l )

进一步变形，变为

\oint_{L}(\frac{\vec B}{\mu_0} -\vec M)d \vec l=I

磁场强度

我们定义磁场强度

\vec H=\frac{\vec B}{\mu_0} -\vec M

所以就得到了有介质的安培环路定律

磁化率 磁导率 相对磁导率

现实生活中的应用

考虑到现实生活中的应用，在线性的各向同性的介质中

我们假设

\vec M=X_m \vec H

其中X_m称为磁化率

\vec B=\mu_0 \vec H+\mu_0 X_m \vec H= \mu_0(1+X_m)\vec H

我们假设\mu=\mu_0(1+X_m),1+X_m=\mu_r

其中\mu称为磁导率（有手册可以查）

\mu_r称为相对磁导率（相对于真空而言）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/439543.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

SAR型ADC结构原理

SAR型ADC结构原理

SAR型 ADC，即逐次渐进逼近型 ADC，采用的是多次比较的方式来获得最终的输出结果，具有简单易用，功耗低的特点。下图这个结构可以帮助我们容易地理解SAR型 ADC的工作过程： 如上图，假设输入信号的伪代码为 45&…
阅读更多...
YOLOv5+单目测距（python）

YOLOv5+单目测距（python）

YOLOv5单目测距（python） 1. 相关配置2. 测距原理3. 相机标定3.1：标定方法13.2：标定方法2 4. 相机测距4.1 测距添加4.2 细节修改（可忽略）4.3 主代码 5. 实验效果 相关链接 1. YOLOV7 单目测距（p…
阅读更多...
今晚直播 | 思码逸陆春蕊：面对研发效能度量落地难点，如何让数据说话？

今晚直播 | 思码逸陆春蕊：面对研发效能度量落地难点，如何让数据说话？

本期分享 本期 DevData Talks 邀请到了思码逸高级咨询专家陆春蕊老师。陆春蕊老师曾就职于 Oracle 美国，在软件质量、项目管理方面有着丰富的经验。在研发效能领域为上百家客户提供了技术、数据分析、实践落地等方面的咨询，协助客户提升研发效能10%-30%…
阅读更多...
Revit问题：墙体被楼板剪切及材质库被锁定问题

Revit问题：墙体被楼板剪切及材质库被锁定问题

一、Revit 墙体被楼板剪切怎么办? 建模的时候画的墙总是到楼板就停了，这是为什么？明明顶部约束到标高2了，这种情况如何解决？ 首先来分析问题产生的原因是，我们在绘制楼板的时候选择了用楼板剪切重复部分的墙体。 解决…
阅读更多...
junit的基本使用

junit的基本使用

1 依赖引入&#xff1a; 只需要在maven项目中引入&#xff1a; <dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>4.12</version> </dependency> 2 常用注解 Test Before after BeforeClass…
阅读更多...
BUG——DM -3217: 第1 行附近出现错误: 列[***]未编制全文索引或全文索引数据错误（全文索引、是否包含某些字符串）

BUG——DM -3217: 第1 行附近出现错误: 列[***]未编制全文索引或全文索引数据错误（全文索引、是否包含某些字符串）

文章目录 一、情景二、报错三、解决四、说明1、CONTAINS的使用前景2、全文索引2.1.全文索引定义语句2.2.全文索引修改语句2.3.全文索引删除语句 一、情景 统计某字段中&#xff0c;包含某些字符串的行数 # 使用CONTAINS select sum(case when CONTAINS(my_column,123) then 1…
阅读更多...
12种优雅的接口优化方案

12种优雅的接口优化方案

12种优雅的接口优化方案 一、背景二、接口优化方案总结1.批处理2.异步处理3.空间换时间4.预处理5.池化思想6.串行改并行7.索引8.避免大事务9.优化程序结构10.深分页问题11.SQL优化12.锁粒度避免过粗欲速则不达，欲达则欲速！ —— 佚名 一、背景 针对老项目，做了许多降本增效…
阅读更多...
4、Symbol-ES6新基础类型

4、Symbol-ES6新基础类型

symbol是 ES6 新增的一种基本数据类型&#xff0c;它和 number、string、boolean、undefined 和 null 是同类型的&#xff0c;object 是引用类型。它用来表示独一无二的值&#xff0c;通过 Symbol 函数生成。 本小节代码都是纯JavaScript代码&#xff0c;建议在非TypeScript环境…
阅读更多...
Rasa实现百度UNIT智能客服教学机器人

Rasa实现百度UNIT智能客服教学机器人

背景 上一篇文章提到了百度UNIT智能客服教学机器人&#xff0c;下面用Rasa实现同样的效果。环境如下 Rasa Version : 3.1.0 Minimum Compatible Version: 3.0.0 Rasa SDK Version : 3.1.1 Rasa X Version : 1.1.0 Python Version : …
阅读更多...
【LeetCode: 354. 俄罗斯套娃信封问题 | 暴力递归=＞记忆化搜索=＞动态规划+二分】

【LeetCode: 354. 俄罗斯套娃信封问题 | 暴力递归=＞记忆化搜索=＞动态规划+二分】

&#x1f680; 算法题 &#x1f680; &#x1f332; 算法刷题专栏 | 面试必备算法 | 面试高频算法 &#x1f340; &#x1f332; 越难的东西,越要努力坚持&#xff0c;因为它具有很高的价值&#xff0c;算法就是这样✨ &#x1f332; 作者简介&#xff1a;硕风和炜&#xff0c;…
阅读更多...
2023年4月份上新的目标检测系列论文（附下载链接）

2023年4月份上新的目标检测系列论文（附下载链接）

来源&#xff1a;投稿 作者&#xff1a;王老师 编辑&#xff1a;学姐 目标检测-预训练相关 论文标题&#xff1a;DetCLIPv2: Scalable Open-Vocabulary Object Detection Pre-training via Word-Region Alignment 论文链接&#xff1a; https://arxiv.org/abs/2304.04514代码链…
阅读更多...
Auto-GPT免费尝鲜之初体验-使用攻略和总结

Auto-GPT免费尝鲜之初体验-使用攻略和总结

Auto-GPT免费尝鲜之初体验-使用攻略和总结 写在前面的废话一、部署 Auto-GPT二、试运行 Auto-GPT三、我踩过的坑四、后续探索 写在前面的废话 ChatGPT 的交互模式&#xff0c;是和一个 “人” 对话聊天。 如果你想了解更多ChatGPT和AI绘画的相关知识&#xff0c;请参考&#…
阅读更多...
【代码调试】《Frustratingly Simple Few-Shot Object Detection》

【代码调试】《Frustratingly Simple Few-Shot Object Detection》

更多问题可参考&#xff1a; https://blog.csdn.net/qiankendeNMY/article/details/128450196 论文地址&#xff1a;https://arxiv.org/abs/2003.06957 论文代码&#xff1a;https://github.com/ucbdrive/few-shot-object-detection 我的配置&#xff1a; Python &#xff1a…
阅读更多...
从零开始，详解亚马逊店铺注册流程及技巧指南

从零开始，详解亚马逊店铺注册流程及技巧指南

近几年跨境电商的势头越来越猛&#xff0c;所以很多新手都想去闯荡一番。很多人的第一选择都是亚马逊&#xff0c;毕竟亚马逊是世界上最大的电商平台之一&#xff0c;因此今天东哥就跟大家分享亚马逊店铺的注册方法&#xff0c;想在亚马逊开店的朋友不要错过&#xff01; 亚马逊…
阅读更多...
设计模式 -- 工厂方法模式以及抽象工厂模式

设计模式 -- 工厂方法模式以及抽象工厂模式

前言 月是一轮明镜,晶莹剔透,代表着一张白纸(啥也不懂) 央是一片海洋,海乃百川,代表着一块海绵(吸纳万物) 泽是一柄利剑,千锤百炼,代表着千百锤炼(输入输出) 月央泽,学习的一种过程,从白纸->吸收各种知识->不断输入输出变成自己的内容 希望大家一起坚持这个过程,也同…
阅读更多...
Mysql MVCC实现

Mysql MVCC实现

文章目录 背景MVCC定义快照读和当前读当前读快照读 MVCC实现原理隐式字段undo log版本链1.插入一条记录2.修改记录3.修改记录 Read View读视图属性&#xff1a;Read View可见性算法 隔离级别长事务为什么要避免长事务 背景 并发事务可能产生的问题&#xff1a; 读读&#xff…
阅读更多...
zk111111111111111111

zk111111111111111111

Zookeeper 1 zookeeper(作为 dubbo 的注册中心): 概述: zookeper 是 一个分布式的、开源的分布式应用程序的协调服务,管理分布式应 用 作用: 配置管理,分布式锁,集群管理 2 zookeeper 的安装 (dubbo 的资料中已经整理) 3 zookeeper 的数据模型 zookeeper 是一个树形的服…
阅读更多...
微信小程序php+vue 校园租房指南房屋租赁系统

微信小程序php+vue 校园租房指南房屋租赁系统

本着诚信的原则&#xff0c;平台必须要掌握出租方必要的真实可信的信息&#xff0c;这样就可以防止欺诈事件的发生&#xff0c;事后也可以联系找到出租方。并且租金等各方面规范标准化&#xff0c;在这易租房诚信可信的平台让承租方与出租方充分有效对接&#xff0c;既方便了承…
阅读更多...
扫清盲点：带你学习 树状数组 这种数据结构

扫清盲点：带你学习 树状数组 这种数据结构

什么是树状数组 树状数组是一种用于维护数列前缀和的数据结构&#xff0c;它可以在 O(logn) 的时间复杂度内修改单个元素的值&#xff0c;以及查询某个区间的元素和。 树状数组的特点是什么&#xff1f; 树状数组的特点其实就是&#xff0c;在单点修改 &#xff0c;和区间查询…
阅读更多...
rancher2.7丢失集群信息

rancher2.7丢失集群信息

使用Docker 单节点安装rancher&#xff0c;然后在rancher中创建了一个k8s的集群。重启rancher所在的虚拟机后&#xff0c;登录rancher发现这是新的实例&#xff0c;集群信息丢失了。但是k8s集群还是好好的。 检查k8s的日志&#xff0c;api server日志会报错 time"2023-0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023