前言
二叉搜索树本质也是二叉树,但因为其数据存储的特殊 —
左子树的值都更小,右子树的值都更大,所以在大部分情况下,查找更为高效。本篇博客将讲述二叉搜索树两个应用搜索的场景
那么话不多说,马上开始今天的学习。

文章目录
- 前言
- 一. Key的模型
- 二. Key_Value的模型
- 结束语
一. Key的模型
Key的模型本质其实是在不在的问题
- 比如:
门禁系统。当我们在进出学校时,可能需要刷校园卡,那其实校园卡里面有芯片,跟门禁交互后,可以读取到你的信息,然后拿着这个信息,去数据库中查找,找到了,那就允许通行,找不到,就不允许通行。- 再比如:
车库系统。如果你有这个车库的停车位,那么你进出车库,车库的杆子直接就抬起,放行。但是如果你没有车位,那么你进入停车场依然抬杆,但是你出来时候,需要支付停车费才能抬杆。这也涉及到了信息的查找和匹配。
最普通的二叉搜索树就是Key的模型,每个节点只存储一个数据,且其实际意义就是那个数据的意义
比如下面这个二叉搜索树,其意义就是整型数字的存储。
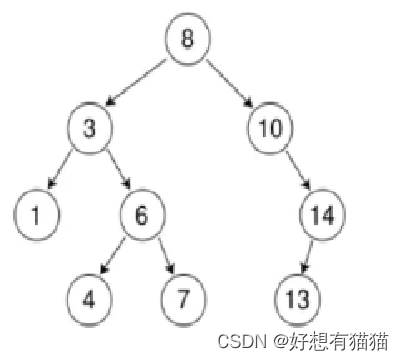
二叉搜索树Key模型的代码在【C++】二叉搜索树
二. Key_Value的模型
Key_Value的模型其实是
映射关系,Key不再单纯只有Key的意义,其还对应了一个Value。
就像一把钥匙,他不仅是一把钥匙,他还有对应一个锁。我们的学号不仅是一串数字,他在学生信息管理系统中,还对应着我们的信息。
比如,我们要完成一个中英文互译的字典,就可以使用Key_Value模型,我们输入的Key是“sort”,对应的Value就是“排序”。
以下我们简单编写一下二叉搜索树的Key_Value模型的代码。其实基本框架和Key模型一样,只是类模板参数多了一个模板参数
//类模板,用于存储不同数据
template<class K,class V>
struct BinarySearchTree
{
BinarySearchTree<K,V>*_left;//左子树
BinarySearchTree<K,V>*_right;//右子树
K _key;//key值
V _value;//value值
//构造函数
BinarySearchTree(const K&key,const V&value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
,_value(value)
{}
~BinarySearchTree()
{
_left = nullptr;
_right = nullptr;
}
};
template<class K,class V>
class BSTree
{
typedef BinarySearchTree<K,V> Node;
public:
//析构
~BSTree()
{
Destroy(_root);
_root = nullptr;
}
//插入
bool Insert(const K&key,const V&value)
{
//头为空时单独处理
if (_root == nullptr)
{
_root = new Node(key,value);
return true;
}
//循环找插入的位置
Node*cur = _root;
//记录父节点,实现链接
Node*parent = nullptr;
while (cur)
{
parent = cur;
if (key > cur->_key)
cur = cur->_right;
else if (key < cur->_key)
cur = cur->_left;
else
//相等则返回假
return false;
}
//找到了要插入的位置
cur = new Node(key,value);
//链接
if (key > parent->_key)
parent->_right = cur;
else
parent->_left = cur;
return true;
}
//中序遍历
//因为二叉搜索树的特点,中序打印出来就是升序
//实现封装
void InOrder()
{
_InOrder(_root);
cout << endl;
}
//查找
Node* Find(const K&key)
{
Node*cur = _root;
//循环查找
while (cur)
{
//比当前值小,则往左走
if (key < cur->_key)
cur = cur->_left;
else if (key > cur->_key)//大则往右走
cur = cur->_right;
else//不然就是相等,相等就是找到了
return cur;
}
//循环没返回说明没查到
return nullptr;
}
//删除
bool Erase(const K&key)
{
//分成两类
//左或者右为空(包括叶子结点)
//左右孩子都有
//首先先找节点
Node*cur = _root;
//记录父亲节点
Node*parent = nullptr;
while (cur)
{
//parent = cur;
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
//找到了
//分两种情况
//左为空
if (cur->_left == nullptr)
{
//还有可能删到根节点的一边为空(有点像歪脖子树)
if (cur == _root)
_root = cur->_right;
else
{
//要判断父节点链接左还右
if (parent->_left == cur)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
delete cur;
cur = nullptr;
return true;
} // 右为空
else if (cur->_right == nullptr)
{
//还有可能删到根节点的一边为空(有点像歪脖子树)
if (cur == _root)
_root = cur->_left;
else
{
//要判断父节点链接左还右
if (parent->_left == cur)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
delete cur;
cur = nullptr;
return true;
}
else
{
//左右子树都不为空
//找保姆
//左子树的最大节点 or 右子树的最小节点 二者都可以
// 最右节点 最左节点
Node*pMinRight = cur;//右子树的最小节点的父节点
Node*MinRight = cur->_right;//右子树的最小节点
while (MinRight->_left)
{
pMinRight = MinRight;
MinRight = MinRight->_left;
}
//直接赋值
cur->_key = MinRight->_key;
//判断父节点要链接左还是右
if (pMinRight->_left == MinRight)
pMinRight->_left = MinRight->_right;
else
pMinRight->_right = MinRight->_right;
//删除MinRight,因为完成交换了
delete MinRight;
MinRight = nullptr;
return true;
}
}
}
return false;
}
protected:
//销毁二叉搜索树
void Destroy(Node*root)
{
if (root == NULL)
return;
//先删除左右节点,再删除当前节点
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}
//因为要递归,所以要单独编写
//注意此处不可以加缺省值_root,因为缺省值需要是常量
void _InOrder(Node*root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
private:
Node*_root = nullptr;//根节点
};
我们以英汉互译为例子,测试一下
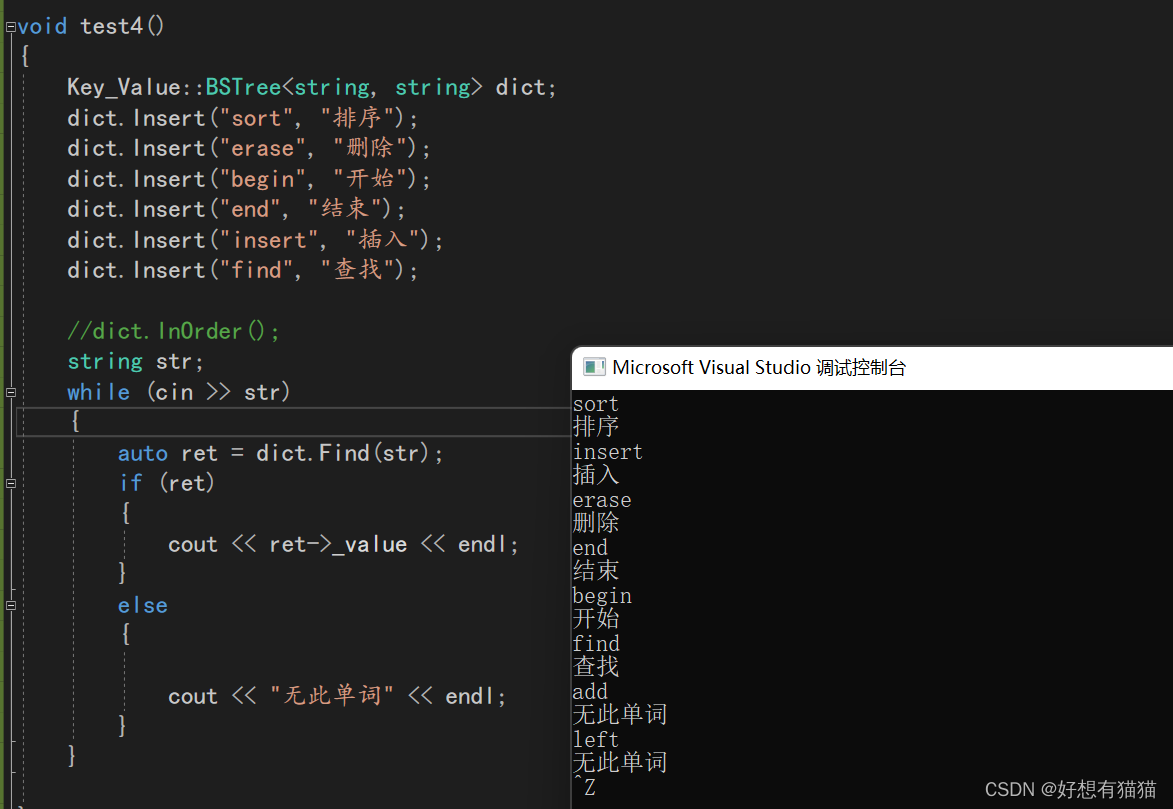
ctrl+z+回车可以正常结束这样的循环
结束语
感谢你的阅读
如果觉得本篇文章对你有所帮助的话,不妨点个赞支持一下博主,拜托啦,这对我真的很重要。