【线性dp 例题 大综合】dp——数字三角形模型【线性dp】

news2024/9/26 1:24:22

数字三角形模型

  • 一、数字三角形模型
        • 1. 摘花生(最大值)
        • 2. 最低通行费(需要把边界置成0x3f)
            • 我的错题点
        • 3. ★★★ 取方格数
            • 路径长度为k,第一条路线到x1=i,第二条路线到x2=j的所有方案
        • 4. ★★★★★ 传纸条
            • 就是 取方格数 的 题意延申一下
  • 0x51 线性dp
        • 经典例题：LIS LCS 数字三角形
        • ✔例1. ★★★ Mr Young's Picture Permutations
            • f[a][b][c][d][e]代表从后往前每排人数分别为a, b, c, d, e的所有方案的集合, 其中a >= b >= c >= d >= e
        • ✔例2. 最长公共上升子序列
            • a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合
            • 关键思路
        • ✔例3. 分级
            • f[i][j] 代表所有给A[1] ~ A[i]分配好了值且最后一个B[i] = A'[j]的方案的集合；
        • ✔例4. 移动服务
            • f[i][x][y]表示已经处理完前i个请求，且三个服务员分别在p[i], x, y的所有方案的集合；
        • ✔例5. 传纸条
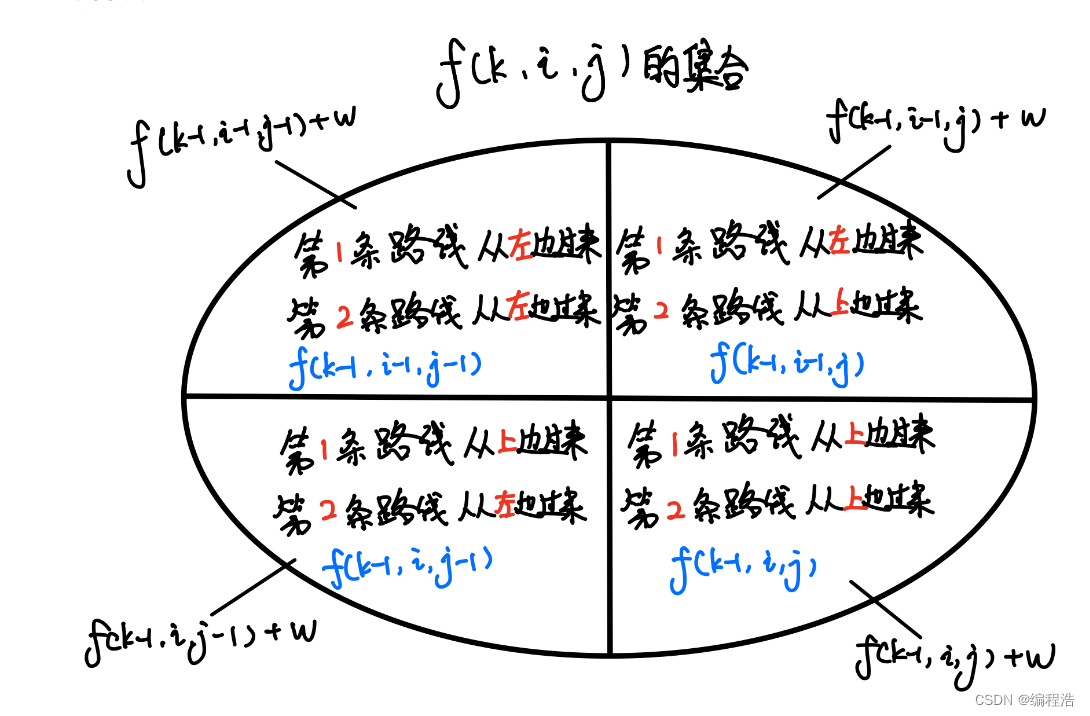
            • f[k, i, j] 表示两个人同时走了k步，第一个人在 (i, k - i) 处，第二个人在 (j, k - j)处的所有走法的最大分值。
            • ✔补充相关例题：取方格数
            • 路径长度为k,第一条路线到x1=i,第二条路线到x2=j的所有方案
        • ✔例6. I-区域★★★★★
        • ✔例7. 饼干
  • 二、线性DP
        • 1. 数字三角形 ✔1.6
        • 2. ☆ 最长上升子序列
            • 双重循环
            • f[i] 以第i个数结尾的 上升子序列的最大值
        • 3. ☆ 最长上升子序列 II
            • ★f[i] 存储 最长上升子序列的 示范串
            • ★ 二分 + dp优化
        • 4. ☆ 最长公共子序列
            • ★f[i][j]表示a的前i个字母，和b的前j个字母的最长公共子序列长度
            • 思路 (在推导示例时，可以总结出)
        • 5. ☆ 最短编辑距离
            • ★f[i][j] 所有把a中的前i个字母 变成 b中前j个字母的集合的操作集合
            • 做题总结
        • 6. 编辑距离( 和上题差不多 )

一、数字三角形模型

1. 摘花生(最大值)

原题链接
原题链接

#include<iostream>

using namespace std;

const int N = 1010;

int f[N][N];
int n;

int main()
{
    cin >> n;
    while(n--)
    {
        int x,y;
        cin >> x >> y;
        for(int i = 1; i <= x; i++)
        {
            for(int j = 1; j <= y; j++)
            {
                cin >> f[i][j];
            }
        }
        
        for(int i = 1; i <= x; i++)
        {
            for(int j = 1; j <= y; j++)
            {
                f[i][j] += max(f[i-1][j],f[i][j-1]);
            }
        }
        cout << f[x][y] << endl;
    }
    
    return 0;
}

2. 最低通行费(需要把边界置成0x3f)

我的错题点
  1. 数组开大一点
  2. 这个题求的是最小值，所以需要把临界值置成最大值
    原题链接
    原题链接
#include<iostream>

using namespace std;

const int N = 110;

int g[N][N];
int f[N][N];
int n,m;

int main()
{
    cin >> n;
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            cin >> g[i][j];
            
    for(int i = 2; i <= n; i++)
        f[0][i] = 0x3f3f3f3f,f[i][0] = 0x3f3f3f3f;
            
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
        {
            f[i][j] = min(f[i-1][j],f[i][j-1]) + g[i][j];
        }
        
    cout << f[n][n];
    
    return 0;
}

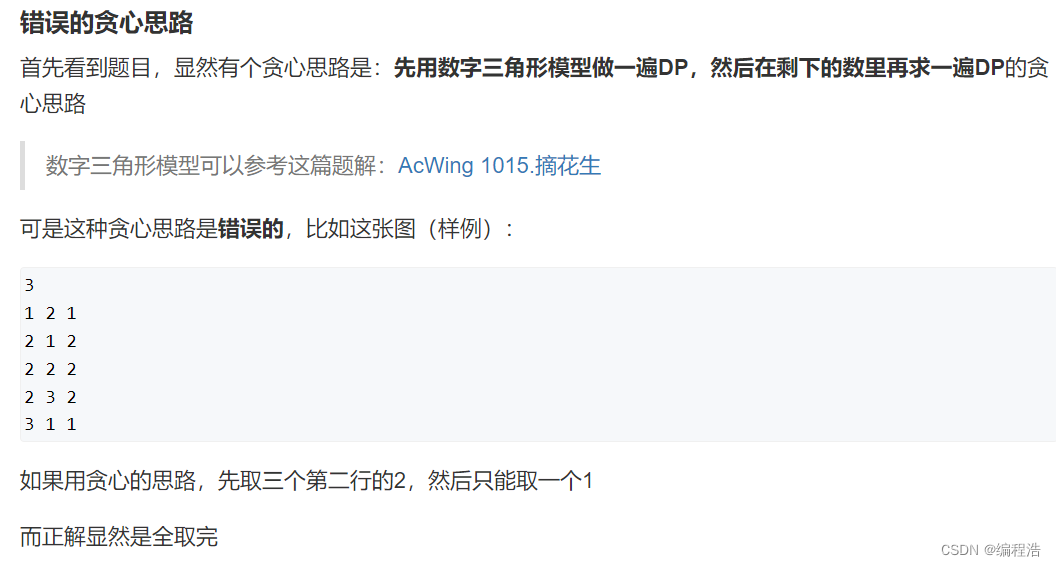
3. ★★★ 取方格数

路径长度为k,第一条路线到x1=i,第二条路线到x2=j的所有方案

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

原题链接

#include <bits/stdc++.h>

using namespace std;

const int N = 15, M = 2 * N;

int n;//方格图的边长 
int w[N][N];
int f[M][N][N];

int get(int i, int j, int k)
{
    return max(max(f[k - 1][i - 1][j - 1], f[k - 1][i][j - 1]), max(f[k - 1][i - 1][j], f[k - 1][i][j]));
    //转移方程，分成 4 种考虑
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n;

    int x, y, z;
    while (cin >> x >> y >> z, x || y || z) w[x][y] += z;

    for (int k = 2; k <= 2 * n; ++ k)
        for (int i = 1; i < k; ++ i)
            for (int j = 1, v; j < k; ++ j)
            {
                f[k][i][j] = get(i, j, k) + w[i][k - i];
                if (i != j) f[k][i][j] += w[j][k - j];//!!!
            }

    cout << f[2 * n][n][n] << endl;
    return 0;
}

4. ★★★★★ 传纸条

就是 取方格数 的 题意延申一下

原题链接
原题链接

#include <bits/stdc++.h>

using namespace std;

const int N = 59, M = 2 * N;

int n, m;//方格图的边长 
int w[N][N];
int f[M][N][N];

int get(int i, int j, int k)
{
    return max(max(f[k - 1][i - 1][j - 1], f[k - 1][i][j - 1]), max(f[k - 1][i - 1][j], f[k - 1][i][j]));
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n >> m;

    int x, y, z;
    for(int i = 1;i <= n;++ i)
        for(int j = 1;j <= m;++ j)
            cin >> w[i][j];

    for (int k = 2;k <= m + n;++ k)
        for (int i = 1;i < k;++ i)
            for (int j = 1;j < k;++ j)
            {
                f[k][i][j] = get(i, j, k) + w[i][k - i];
                if (i != j) f[k][i][j] += w[j][k - j];
            }

    cout << f[m + n][n][n] << endl;
    return 0;
}

0x51 线性dp

在这里插入图片描述

经典例题：LIS LCS 数字三角形

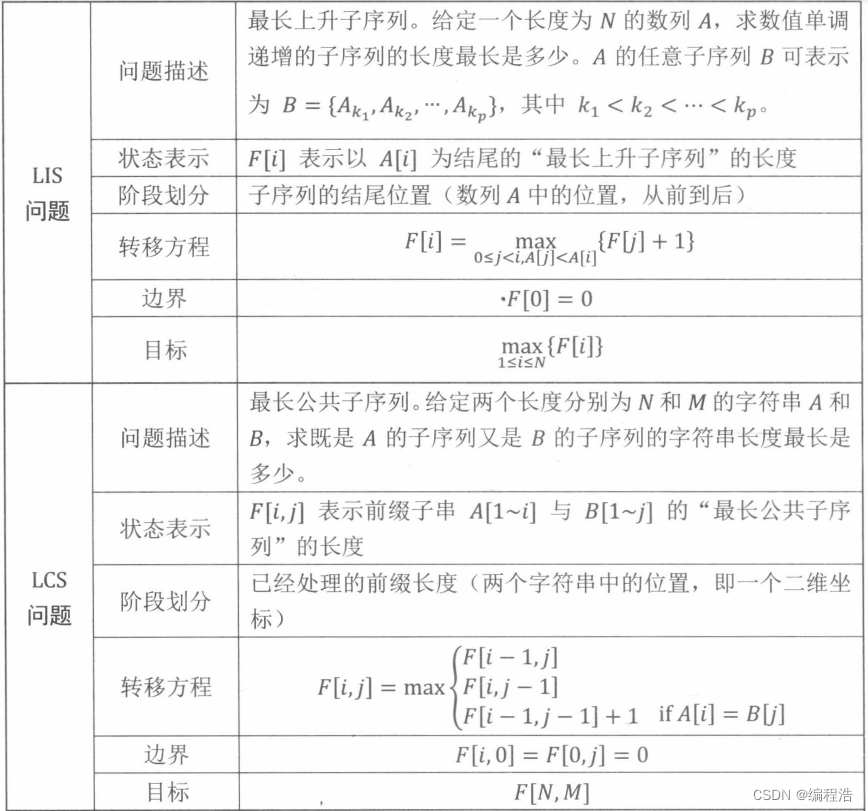
在这里插入图片描述在这里插入图片描述

✔例1. ★★★ Mr Young’s Picture Permutations

原题链接
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

f[a][b][c][d][e]代表从后往前每排人数分别为a, b, c, d, e的所有方案的集合, 其中a >= b >= c >= d >= e
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 31;

int n;
LL f[N][N][N][N][N];

int main()
{
    while (cin >> n, n)
    {
        int s[5] = {0};
        for (int i = 0; i < n; i ++ ) cin >> s[i];
        memset(f, 0, sizeof f);
        f[0][0][0][0][0] = 1;

        for (int a = 0; a <= s[0]; a ++ )
            for (int b = 0; b <= min(a, s[1]); b ++ )
                for (int c = 0; c <= min(b, s[2]); c ++ )
                    for (int d = 0; d <= min(c, s[3]); d ++ )
                        for (int e = 0; e <= min(d, s[4]); e ++ )
                        {
                            LL &x = f[a][b][c][d][e];
                            if (a && a - 1 >= b) x += f[a - 1][b][c][d][e];
                            if (b && b - 1 >= c) x += f[a][b - 1][c][d][e];
                            if (c && c - 1 >= d) x += f[a][b][c - 1][d][e];
                            if (d && d - 1 >= e) x += f[a][b][c][d - 1][e];
                            if (e) x += f[a][b][c][d][e - 1];
                        }
        cout << f[s[0]][s[1]][s[2]][s[3]][s[4]] << endl;
    }

    return 0;
}

作者：yxc
链接：https://www.acwing.com/solution/content/4954/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

✔例2. 最长公共上升子序列

原题链接

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合
#include <cstdio>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &b[i]);

    for (int i = 1; i <= n; i ++ )
    {
        int maxv = 1;
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
            if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
        }
    }

    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
    printf("%d\n", res);

    return 0;
}

作者：yxc
链接：https://www.acwing.com/solution/content/4955/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
关键思路
  1. dp很复杂，以bi结尾fi，j这样就会减少复杂度
  2. maxv记录是什么
    由普遍算法 推广到 优化代码的过程理解了 就知道maxv存储的是什么了

✔例3. 分级

原题链接

比较不错的题解

f[i][j] 代表所有给A[1] ~ A[i]分配好了值且最后一个B[i] = A’[j]的方案的集合；

在这里插入图片描述
在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

const int N = 2010, INF = 0x3f3f3f3f;

int n;
int a[N], s[N];
int f[N][N];
int ans;

int work()
{
    for (int i = 1; i <= n; i ++ ) s[i] = a[i];
    sort(s + 1, s + 1 + n);
    for (int i = 1; i <= n; i ++ )
    {
        int mn = INF;
        for (int j = 1; j <= n; j ++ )
        {
            mn = min(mn, f[i - 1][j]);
            f[i][j] = mn + abs(a[i] - s[j]);
        }
    }
    int res = INF;
    for (int i = 1; i <= n; i ++ ) res = min(res, f[n][i]);
    return res;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    ans = work();
    reverse(a + 1, a + 1 + n);
    ans = min(ans, work());
    printf("%d\n", ans);
    return 0;
}

作者：种花家的兔兔
链接：https://www.acwing.com/solution/content/136108/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

✔例4. 移动服务

f[i][x][y]表示已经处理完前i个请求，且三个服务员分别在p[i], x, y的所有方案的集合；

在这里插入图片描述

原题链接
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 210, M = 1010, INF = 0x3f3f3f3f;

int n, m;
int w[N][N];
int f[M][N][N];
int p[M];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            scanf("%d", &w[i][j]);
    for (int i = 1; i <= m; i ++ ) scanf("%d", &p[i]);

    p[0] = 3;
    memset(f, 0x3f, sizeof f);
    f[0][1][2] = 0;
    for (int i = 0; i < m; i ++ )
        for (int x = 1; x <= n; x ++ )
            for (int y = 1; y <= n; y ++ )
            {
                int z = p[i], v = f[i][x][y];
                if (x == y || x == z || y == z) continue;
                int u = p[i + 1];
                f[i + 1][x][y] = min(f[i + 1][x][y], v + w[z][u]);
                f[i + 1][z][y] = min(f[i + 1][z][y], v + w[x][u]);
                f[i + 1][x][z] = min(f[i + 1][x][z], v + w[y][u]);
            }

    int res = INF;
    for (int x = 1; x <= n; x ++ )
        for (int y = 1; y <= n; y ++ )
        {
            int z = p[m];
            if (x == y || x == z || y == z) continue;
            res = min(res, f[m][x][y]);
        }

    printf("%d\n", res);

    return 0;
}

作者：yxc
链接：https://www.acwing.com/solution/content/4957/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

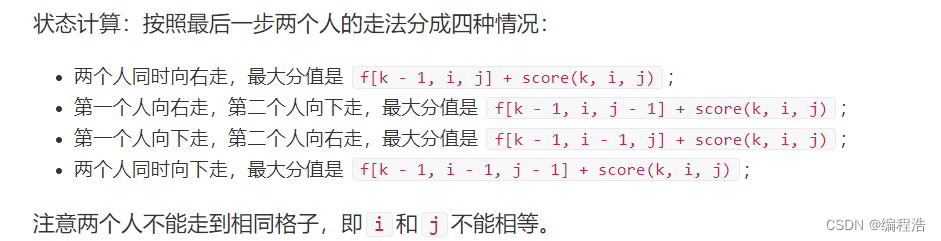
✔例5. 传纸条

f[k, i, j] 表示两个人同时走了k步，第一个人在 (i, k - i) 处，第二个人在 (j, k - j)处的所有走法的最大分值。

原题链接

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 55;

int n, m;
int g[N][N];
int f[N * 2][N][N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &g[i][j]);

    for (int k = 2; k <= n + m; k ++ )
        for (int i = max(1, k - m); i <= n && i < k; i ++ )
            for (int j = max(1, k - m); j <= n && j < k; j ++ )
                for (int a = 0; a <= 1; a ++ )
                    for (int b = 0; b <= 1; b ++ )
                    {
                        int t = g[i][k - i];
                        if (i != j || k == 2 || k == n + m)
                        {
                            t += g[j][k - j];
                            f[k][i][j] = max(f[k][i][j], f[k - 1][i - a][j - b] + t);
                        }
                    }

    printf("%d\n", f[n + m][n][n]);

    return 0;
}

作者：yxc
链接：https://www.acwing.com/solution/content/3954/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
✔补充相关例题：取方格数
路径长度为k,第一条路线到x1=i,第二条路线到x2=j的所有方案

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

原题链接

#include <bits/stdc++.h>

using namespace std;

const int N = 15, M = 2 * N;

int n;//方格图的边长 
int w[N][N];
int f[M][N][N];

int get(int i, int j, int k)
{
    return max(max(f[k - 1][i - 1][j - 1], f[k - 1][i][j - 1]), max(f[k - 1][i - 1][j], f[k - 1][i][j]));
    //转移方程，分成 4 种考虑
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n;

    int x, y, z;
    while (cin >> x >> y >> z, x || y || z) w[x][y] += z;

    for (int k = 2; k <= 2 * n; ++ k)
        for (int i = 1; i < k; ++ i)
            for (int j = 1, v; j < k; ++ j)
            {
                f[k][i][j] = get(i, j, k) + w[i][k - i];
                if (i != j) f[k][i][j] += w[j][k - j];//!!!
            }

    cout << f[2 * n][n][n] << endl;
    return 0;
}

✔例6. I-区域★★★★★

原题链接
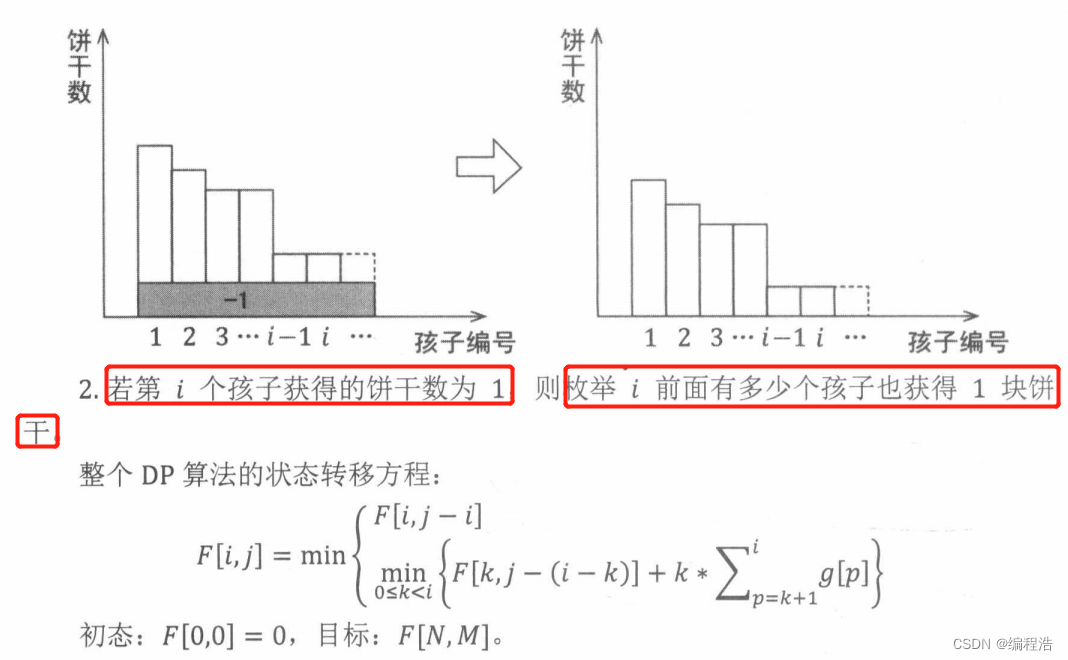
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

✔例7. 饼干

原题链接
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

二、线性DP

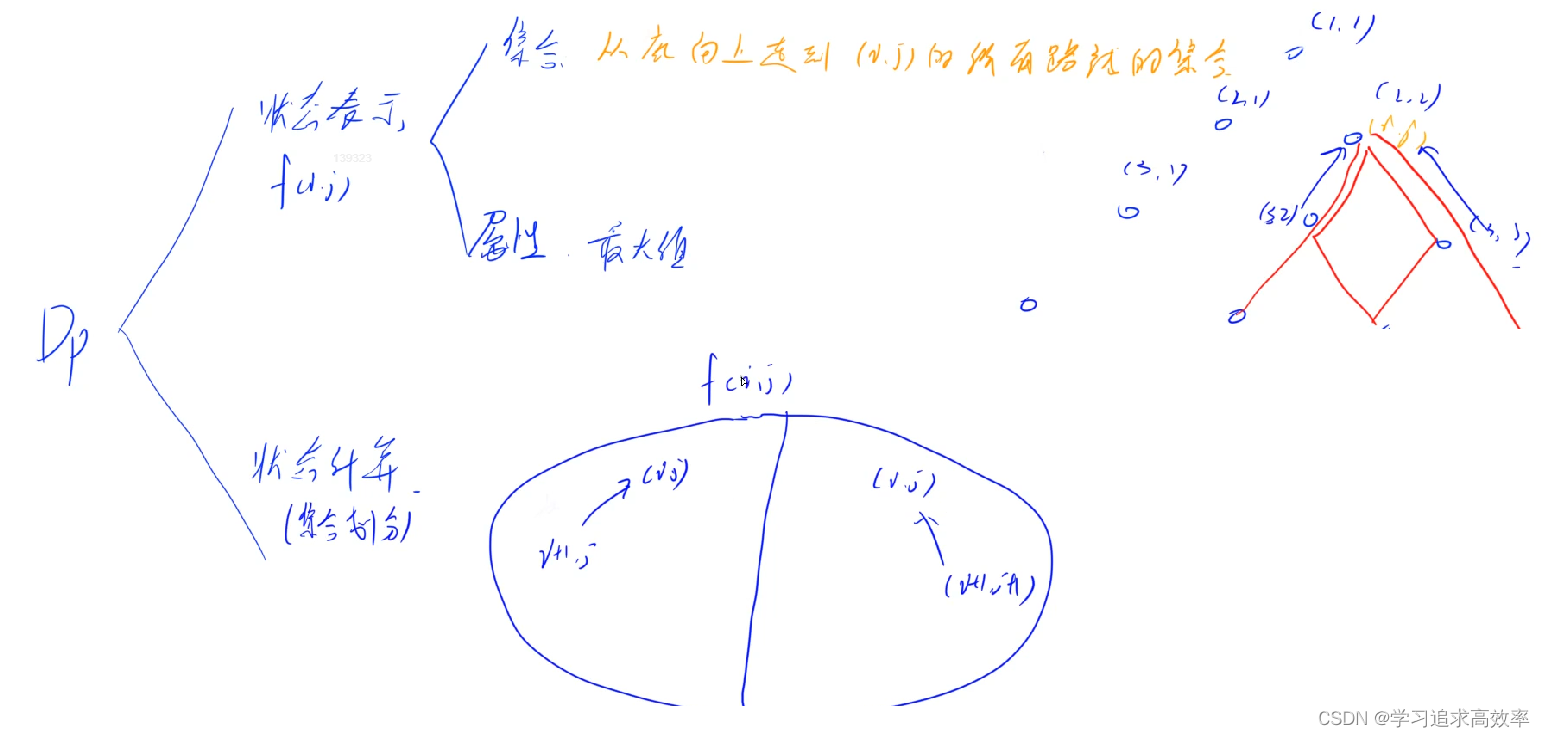
1. 数字三角形 ✔1.6

★f[i][j] 从下到上 走到f[i][j]的所有路径的最大值
原题链接
原题链接
在这里插入图片描述

#include<iostream>

using namespace std;

const int N = 510;

int f[N][N];

int main()
{
    int n;
    cin >> n;
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= i; j++)
            cin >> f[i][j];
    
    for(int i = n-1; i >= 1; i--)
        for(int j = 1; j <= i; j++)
            f[i][j] += max(f[i+1][j],f[i+1][j+1]);
    
    cout << f[1][1];
    
    return 0;
}

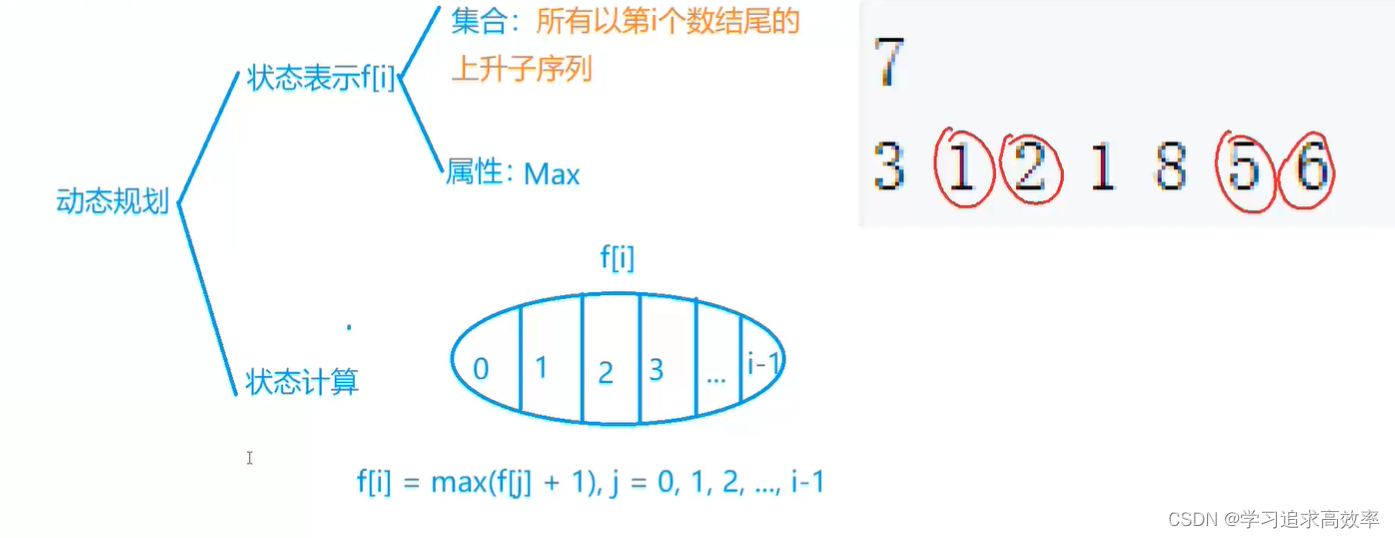
2. ☆ 最长上升子序列

双重循环
f[i] 以第i个数结尾的 上升子序列的最大值

原题链接

在这里插入图片描述

#include<iostream>

using namespace std;

const int N = 1010;

int a[N],f[N];

int main()
{
    int n;
    cin >> n;
    
    for(int i = 1; i <= n; i++)
        cin >> a[i];
        
    for(int i = 1; i <= n; i++)
    {
        f[i] = 1;
        for(int j = 1; j <= i; j++)
        {
            if(a[i] > a[j])
                f[i] = max(f[i],f[j]+1);
        }
    }
    
    int res = 0;
    
    for(int i = 1; i <= n; i++)
        res = max(res,f[i]);
        
    cout << res;
    
    return 0;
}

3. ☆ 最长上升子序列 II

★f[i] 存储 最长上升子序列的 示范串
★ 二分 + dp优化

原题链接

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1e5+10;

int n;
int f[N],st[N];

int main()
{
    cin >> n;
    
    for(int i = 1; i <= n; i++) cin >> f[i];
    
    
    int len;
    st[1] = f[1];
    len = 1;
    for(int i = 2; i <= n; i++)
    {
        int pos = lower_bound(st+1,st+1+len,f[i])-st;
        st[pos] = f[i];
        len = max(len,pos);
    }
    

    
    cout << len;
    
    return 0;
}

4. ☆ 最长公共子序列

★f[i][j]表示a的前i个字母，和b的前j个字母的最长公共子序列长度

原题链接

在这里插入图片描述

思路 (在推导示例时，可以总结出)
  1. f[i][j] 表示什么需要先想清楚。
    表示的是：在i，j组合的情况下，的最大子串 长度
    所以当 i，j相等时
    f[i][j] = f[i-1][j-1] + 1
    不相等的时候
    f[i][j] = max(f[i-1][j],f[i][j-1]);
#include<iostream>

using namespace std;

const int N = 1010;

int f[N][N];
int n,m;
char a[N],b[N];

int main()
{
    cin >> n >> m >> a+1 >> b+1;
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            if(a[i]==b[j])
                f[i][j] = f[i-1][j-1] + 1;
            else
                f[i][j] = max(f[i-1][j],f[i][j-1]);
        }
    }
    
    cout << f[n][m];
    
    return 0;
}

5. ☆ 最短编辑距离

原题链接

★f[i][j] 所有把a中的前i个字母 变成 b中前j个字母的集合的操作集合
做题总结
  1. 由于需要用到前面的数据，所以一定用dp
  2. i j 相等则 在 i - 1 j-1 的基础 +1
  3. 如果不相等 则按着 所可以操作的步骤 + 1
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
    scanf("%d%s", &n, a + 1);
    scanf("%d%s", &m, b + 1);

    for (int i = 0; i <= m; i ++ ) f[0][i] = i;
    for (int i = 0; i <= n; i ++ ) f[i][0] = i;

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            if (a[i] == b[j])
            {
                f[i][j] = f[i-1][j-1];
            }
            else
            {
                f[i][j] = min(f[i-1][j] + 1, f[i - 1][j - 1] + 1);
                f[i][j] = min(f[i][j],f[i][j-1]+1);
            }
        }

    printf("%d\n", f[n][m]);

    return 0;
}

6. 编辑距离( 和上题差不多 )

原题链接

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/439203.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Databend v1.1 版本发布！

Databend v1.1 版本发布！

各位社区小伙伴们&#xff0c;Databend 于 2023 年 4 月 14 日迎来了 v1.1.0 版本的正式发布&#xff01; 这次新版本是 Databend 发布1.0 版本之后的第一个大版本&#xff01;相较于 v1.0.0 版本&#xff0c;开发者们一共新增了 1,616 次commit&#xff0c; 共计 505 个优化和…
阅读更多...
程序员跳槽，要求涨薪50%过分吗？

程序员跳槽，要求涨薪50%过分吗？

如果问在TI行业涨工资最快的方式是什么&#xff1f; 回答最多的一定是&#xff1a;跳槽&#xff01; 前段时间&#xff0c;知乎上这样一条帖子引发了不少IT圈子的朋友的讨论 &#xff0c;有网友提问 “程序员跳槽要求涨薪50%过分吗&#xff1f;” 截图来源于知乎&#xff0c;…
阅读更多...
uni-app生成海报并分享

uni-app生成海报并分享

lime-painter是一款canvas海报组件&#xff0c;可以更轻松的生成海报 海报画板 - DCloud 插件市场 一款canvas海报组件&#xff0c;更优雅的海报生成方案https://ext.dcloud.net.cn/plugin?id2389插件提供 JSON 及 Template 的方式绘制海报 1、Template方式 提供l-painter-…
阅读更多...
【Transformer系列（4）】Transformer模型结构超详细解读

【Transformer系列（4）】Transformer模型结构超详细解读

前言 前一篇我们一起读了Transformer的论文《Attention Is All You Need》&#xff0c;不知道大家是否真的理解这个传说中的神&#xff08;反正俺是没有~&#xff09; 这两天我又看了一些视频讲解&#xff0c;感谢各位大佬的解读&#xff0c;让我通透了不少。 这篇文章就和…
阅读更多...
前沿的Web前端技术趋势与应用实践

前沿的Web前端技术趋势与应用实践

近年来&#xff0c;Web前端技术发展迅猛&#xff0c;各种新技术层出不穷&#xff0c;为了跟上潮流&#xff0c;我们需要不断学习新知识&#xff0c;应用新技术&#xff0c;不断提高自己的技术水平&#xff0c;为自己的职业生涯打下坚实的基础。本篇博客将为大家详细介绍前沿的W…
阅读更多...
【Mysql】主从复制

【Mysql】主从复制

【Mysql】主从复制 文章目录 【Mysql】主从复制1. 概述2. 原理3. 搭建3.1 准备工作3.2 主库配置3.3 从库配置 1. 概述 主从复制是指主数据库的 DDL 和 DML 操作通过二进制日志传到从库服务器中&#xff0c;然后再从库上对这些日志重新执行(也叫重做)&#xff0c;从而使得从库和…
阅读更多...
小红书行业趋势分析，女性种草关键词有哪些？

小红书行业趋势分析，女性种草关键词有哪些？

在“她力量”崛起的当今&#xff0c;女性用户正不断引领新潮流&#xff0c;驱动产品、内容升级。女性个人观念、生活方式、消费偏好演变&#xff0c;需求重点势必不断更新。 今儿就女性用户的聚集地小红书平台&#xff0c;以及女性最关注的美妆、母婴两大行业&#xff0c;通过数…
阅读更多...
完整支持Oracle PL/SQL，星环科技KunDB高兼容性实现低成本国产化替代

完整支持Oracle PL/SQL，星环科技KunDB高兼容性实现低成本国产化替代

从中兴、华为等一系列高新科技企业被美国制裁&#xff0c;到俄乌冲突事件爆发后&#xff0c;西方各国相继宣布制裁俄罗斯&#xff0c;以Oracle、IBM、微软、SAP为代表的科技巨头暂停在俄服务&#xff0c;这一系列动作给我们敲响了加速国产化替代的警钟。数据库作为提供数据存储…
阅读更多...
2024年浙大MBA提前批面试即将开始申请，如何操作？

2024年浙大MBA提前批面试即将开始申请，如何操作？

在去年的这个时间点&#xff0c;浙大MBA提前批面试的申请系统已经打开并可以正常开始接受申请报名&#xff0c;而今年的申请时间会在什么时间点&#xff1f;那么又如何准备浙大MBA的提面申请呢&#xff1f;本期专注浙大的杭州达立易考教育为大家做一下梳理&#xff0c;帮助大家…
阅读更多...
【机器学习】P21 正则化 Regularization（L1正则化 Lasso、L2正则化 Ridge、弹性网络正则化、Dropout正则化、早停法）

【机器学习】P21 正则化 Regularization（L1正则化 Lasso、L2正则化 Ridge、弹性网络正则化、Dropout正则化、早停法）

既然模型有概率发生过拟合现象&#xff0c;那么如何才能减少过拟合&#xff0c;或者防止过拟合的产生&#xff1f;方法之一就是正则化方法&#xff0c;Regularization&#xff1b; 我对正则化&#xff0c;有这样的理解&#xff1a;“我们既希望能够通过权重的调整从而建立更好…
阅读更多...
数据结构考研版——括号的匹配问题栈的计算问题

数据结构考研版——括号的匹配问题栈的计算问题

一、括号的匹配问题 这玩意太简单了没什么讲头&#xff0c;就是括号一个一个进栈&#xff0c;匹配就出&#xff0c;以此类推 二、括号匹配问题代码 int isMatched(char left, char right) {if (left (&& right ))return 1;else if (left [ && right ])ret…
阅读更多...
还在发愁项目去哪找？软件测试企业级Web自动化测试实战项目

还在发愁项目去哪找？软件测试企业级Web自动化测试实战项目

今天给大家分享一个简单易操作的实战项目&#xff08;已开源&#xff09; 项目名称 ET开源商场系统 项目描述 ETshop是一个电子商务B2C电商平台系统&#xff0c;功能强大&#xff0c;安全便捷。适合企业及个人快速构建个性化网上商城。 包含PCIOS客户端Adroid客户端微商城…
阅读更多...
Java语法理论和面经杂疑篇《十. 反射机制》

Java语法理论和面经杂疑篇《十. 反射机制》

目录 1. 反射(Reflection)的概念 1.1 反射的出现背景 1.2 反射概述 1.3 Java反射机制研究及应用 1.4 反射相关的主要API 1.5 反射的优缺点 2. 理解Class类并获取Class实例 2.1 理解Class 2.1.1 理论上 2.1.2 内存结构上 2.2 获取Class类的实例(四种方法) 2.3 哪些类…
阅读更多...
设计模式：创建者模式 - 原型模式

设计模式：创建者模式 - 原型模式

文章目录 1.概述2.结构3.实现4.案例5.使用场景6.扩展&#xff08;深克隆&#xff09; 1.概述 用一个已经创建的实例作为原型&#xff0c;通过复制该原型对象来创建一个和原型对象相同的新对象。 2.结构 原型模式包含如下角色&#xff1a; 抽象原型类&#xff1a;规定了具体…
阅读更多...
nodejs+vue宠物商城健康医院挂号服务管理系统python+java+php

nodejs+vue宠物商城健康医院挂号服务管理系统python+java+php

在前台&#xff0c;首先提供一个界面清晰、导航明确的首页&#xff0c;无论是会员还是游客都可以访问。游客通过首页查看该网站所要具备的功能&#xff0c;以及对应的周边商城信息&#xff0c;特别在周边商城模块&#xff0c;需要明确的进行介绍&#xff0c;突出周边商城特色和…
阅读更多...
如何主动增加自己的开源项目star数的方法汇总

如何主动增加自己的开源项目star数的方法汇总

本篇文章主要讲解&#xff0c;通过自媒体、短视频、网络平台等渠道形式增加自己的开源项目的曝光度以增加star数的方法。 作者&#xff1a;任聪聪 日期&#xff1a;2023年4月20日 开源项目的star数在某些找工作的情况下是有一定的加分的&#xff0c;故此价值是一定的。但是自己…
阅读更多...
arm64异常向量表

arm64异常向量表

arm64异常向量表 1 arm64异常向量表2 linux arm64异常向量表3 kernel_ventry宏4 异常向量表的保存4. VBAR_ELx寄存器4.2 __primary_switched4.3 __primary_switched 1 arm64异常向量表 When an exception occurs, the processor must execute handler code which corresponds t…
阅读更多...
电力系统谐波影响及治理

电力系统谐波影响及治理

1.谐波 众所周知&#xff0c;理想的电力系统向用户提供的是一个恒定工频的正弦波形电压&#xff0c;但是由于各种原因&#xff0c;使这种理想状态在实际中无法存在。当正弦波电压施加在非线性电路上时&#xff0c;电流就变成非正弦波&#xff0c;非正弦电流在电网阻抗上产生压…
阅读更多...
机器学习：基于逻辑回归和高斯贝叶斯对人口普查数据集的分类与预测

机器学习：基于逻辑回归和高斯贝叶斯对人口普查数据集的分类与预测

机器学习：基于逻辑回归和高斯贝叶斯对人口普查数据集的分类与预测作者：i阿极 作者简介：Python领域新星作者、多项比赛获奖者：博主个人首页 😊😊😊如果觉得文章不错或能帮助到你学习，可以点赞👍收藏📁评论📒+关注哦！👍👍👍 📜📜📜如果有小伙伴需要…
阅读更多...
【python】采集每日必看黄色软件数据~

【python】采集每日必看黄色软件数据~

前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 环境使用: Python 3.8 Pycharm 模块使用: requests >>> pip install requests re csv 安装模块&#xff1a;win R 输入cmd 输入安装命令 pip install 模块名 如果出现爆红 可能是因为 网络连接超时 切换国内…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023