【1187. 使数组严格递增】

news2024/9/30 9:33:49

来源：力扣（LeetCode）

描述：

给你两个整数数组 arr1 和 arr2，返回使 arr1 严格递增所需要的最小「操作」数（可能为 0）。

每一步「操作」中，你可以分别从 arr1 和 arr2 中各选出一个索引，分别为 i 和 j，0 <= i < arr1.length 和 0 <= j < arr2.length，然后进行赋值运算 arr1[i] = arr2[j]。

如果无法让 arr1 严格递增，请返回 -1。

示例 1：

输入：arr1 = [1,5,3,6,7], arr2 = [1,3,2,4]
输出：1
解释：用 2 来替换 5，之后 arr1 = [1, 2, 3, 6, 7]。

示例 2：

输入：arr1 = [1,5,3,6,7], arr2 = [4,3,1]
输出：2
解释：用 3 来替换 5，然后用 4 来替换 3，得到 arr1 = [1, 3, 4, 6, 7]。

示例 3：

输入：arr1 = [1,5,3,6,7], arr2 = [1,6,3,3]
输出：-1
解释：无法使 arr1 严格递增。

提示：

1 <= arr1.length, arr2.length <= 2000
0 <= arr1[i], arr2[i] <= 10⁹

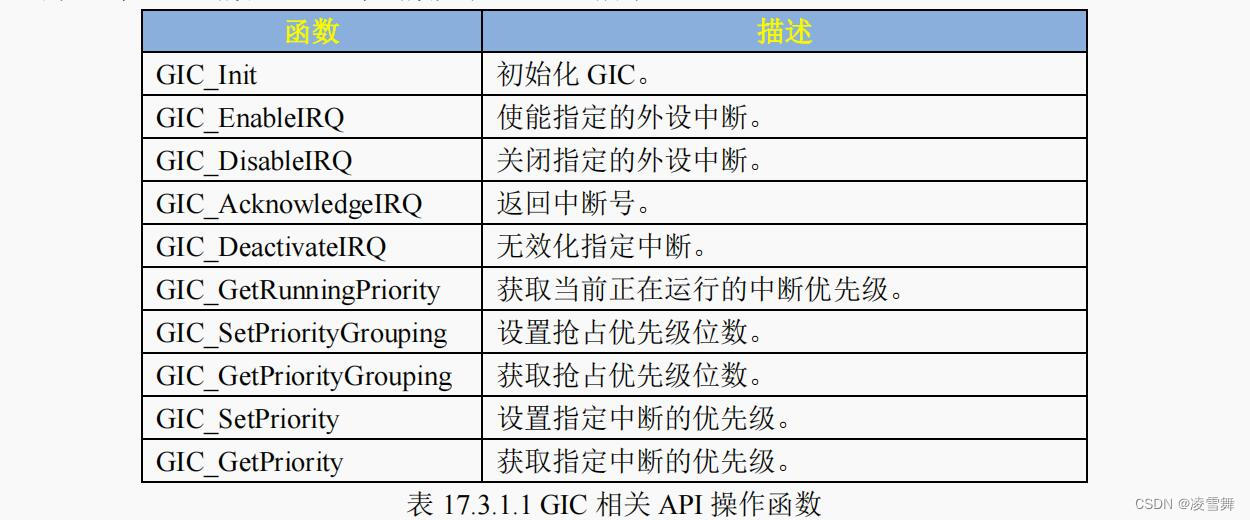
方法：动态规划

思路与算法

首先我们思考一下，由于要求数组严格递增，因此数组中不可能存在相同的元素，对于数组 arr₂ 来说，可以不需要考虑数组中的重复元素，可以预处理去除 arr₂ 的重复元素，假设数组 arr₁ 的长度为 n，数组 arr₂ 的长度为 m，此时可以知道最多可以替换的次数为 min(n, m)。如何才能定义动态规划的递推公式，这就需要进行思考。我们设 dp[i][j] 表示数组 arr₁中的前 i 个元素进行了 j 次替换后组成严格递增子数组末尾元素的最小值。当我们遍历 arr₁的第 i 个元素时，此时 arr₁[i] 要么进行替换，要么进行保留，实际可以分类进行讨论:

此时如果 arr₁[i] 需要进行保留，则 arr₁[i] 一定严格大于前 i − 1 个元素替换后组成的严格递增子数组最末尾的元素。假设前 i − 1 个元素经过了 j 次变换后得到的递增子数组的末尾元素的最小值为 dp[i − 1][j]，如果满足 arr₁[i] > dp[i − 1][j]，则此时 arr₁[i] 可以保留加入到该子数组中且构成的数组严格递增；
此时如果 arr₁[i] 需要进行替换，则替换后的元素一定严格大于前 i − 1 个元素替换后组成的严格递增子数组最末尾的元素。假设前 i − 1 个元素经过了 j − 1 次变换后得到的递增子数组的末尾元素的最小值为 dp[i − 1][j − 1]，此时我们从 arr₂ 找到严格大于 dp[i − 1][j − 1] 的最小元素 arr₂[k]，则此时将 arr₂[k] 加入到该子数组中且构成数组严格递增；
综上可知，每个元素在替换时只有两种选择，要么选择保留当前元素 arr₁ ，要么从 arr₂ 中选择一个满足条件的最小元素加入到数组中，最少替换方案一定包含在上述替换方法中。我们可以得到以下递推关系：

为了便于计算，我们将 dp[i][j] 的初始值都设为 ∞，为了便于计算在最开始加一个哨兵，此时令 dp[0][0] = −1 表示最小值。实际计算过程如下:

为了方便计算，需要对 arr₂ 进行预处理，去掉其中的重复元素，为了快速找到数组 arr₂ 中的最小元素，还需要对 arr₂ 进行排序；
依次尝试计算前 i 个元素在满足 j 次替换时的最小元素：
- 如果当前元素 arr₁[i] 大于 dp[i][j − 1]，此时可以尝试将 arr₁[i] 替换为 dp[i][j]，即此时 dp[i][j] = min(dp[i][j], arr₁[i])。
- 如果前 i − 1 个元素可以满足 j − 1 次替换后成为严格递增数组，即满足 dp[i − 1][j − 1] ≠ ∞，可以尝试在第 j 次替换掉 arr₁[i]，此时根据贪心原则，利用二分查找可以快速的找到严格大于 dp[i − 1][j − 1] 的最小值进行替换即可。
设当前数组 arr₁[i] 的长度为 n，如果前 n 个元素满足 j 次替换后成为严格递增数组，此时我们找到最小的 j 返回即可。

代码：

constexpr int INF = 0x3f3f3f3f;

class Solution {
public:
    int makeArrayIncreasing(vector<int>& arr1, vector<int>& arr2) {
        sort(arr2.begin(), arr2.end());
        arr2.erase(unique(arr2.begin(), arr2.end()), arr2.end());
        int n = arr1.size();
        int m = arr2.size();
        vector<vector<int>> dp(n + 1, vector<int>(min(m, n) + 1, INF));
        dp[0][0] = -1;
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= min(i, m); j++) {
                /* 如果当前元素大于序列的最后一个元素 */
                if (arr1[i - 1] > dp[i - 1][j]) {
                    dp[i][j] = arr1[i - 1];
                }
                if (j > 0 && dp[i - 1][j - 1] != INF) {
                    /* 查找严格大于 dp[i - 1][j - 1] 的最小元素 */
                    auto it = upper_bound(arr2.begin() + j - 1, arr2.end(), dp[i - 1][j - 1]);
                    if (it != arr2.end()) {
                        dp[i][j] = min(dp[i][j], *it);
                    }
                }
                if (i == n && dp[i][j] != INF) {
                    return j;
                }
            }
        }
        return -1;
    }
};

执行用时：48 ms, 在所有 C++ 提交中击败了64.81%的用户
内存消耗：35.6 MB, 在所有 C++ 提交中击败了51.85%的用户
复杂度分析
时间复杂度：O(n × min(m, n) × logm)，其中 n 表示数组 arr₁ 的长度，m 表示数组 arr₂ 的长度。每次替换时，我们都需利用二分查找找到最小的元素，此时需要的时间为 O(logm)，最多需要尝试 n × min(m, n) 种替换方案，因此总的时间复杂度为 O(n × min(m, n) × logm)。
空间复杂度：O(n × min(m, n))，其中 n 表示数组 arr₁ 的长度，m 表示数组 arr₂ 的长度。我们需要保存每个子数组中替换次数下的末尾元素的最大值，一共最多有 n 个子数组，每个子数组替换替换的次数最多为 min(n, m) 次数，因此空间复杂度为 O(n×min(m,n))。
author：LeetCode-Solution