点击蓝字

关注我们
AI TIME欢迎每一位AI爱好者的加入!
╱ 作者简介╱

林隆龙
博士、副教授
目前任职于西南大学计算机与信息科学学院 软件学院。2022年6月于华中科技大学计算机科学与技术学院获博士学位。目前主要研究兴趣包括(时序)社区挖掘、局部聚类、Personalized PageRank计算、图神经网络的可扩展算法设计等领域。目前发表论文于AAAI,TSMC, ICDCS, TBD, DASFAA, JCST等顶级期刊/会议论文
01
内容简介
图聚类是一个重要的算法基础,它被广泛地应用在图像分割、社区发现、机器学习等领域。一般地,图聚类旨在将一个完整的图划分为几个互不重叠的簇,使得每个簇的内部有较稠密的边,而簇之间有较稀疏的边。许多图聚类的模型被提出,比如,模块度、结构聚类以及稠密子图。其中,基于Conductance的图聚类是当今最为主流的一种方式,它有很好的结构性质以及坚固的理论基础。然而,目前的基于Conductance的图聚类算法面临可扩展性低和质量差的困境。为了更好地解决上述困境,我们提出了一种基于Peeling的贪婪计算框架,它能囊括现存方法的计算范式。基于该框架,我们提出了一个高效率的启发式算法PCon_core和一个高效率和高质量的近似算法PCon_de。其中,PCon_de具有线性的时间复杂度和近似线性的近似比。
02
Problem Definition & Applications
Background
图聚类是一个非常重要的理论和实际问题,它旨在将一个图划分为不同的簇,使得簇内部的联系或者边较簇之间的联系更多。用通俗的话解释就是:物以类聚、人以群分。
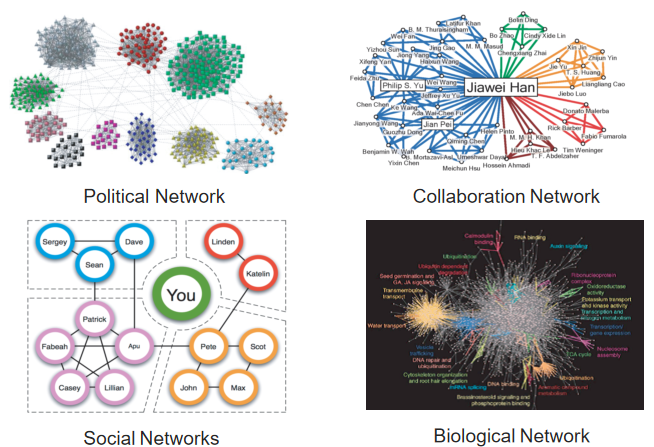
基于这种直观,学者们提出了大量的模型,主要包括两大类。第一类是图论模型,包括Clique、Quasi-Clique、K-truss、K-core、Densest subgraph和K-ECC等。第二类是统计物理模型,包括Betweenness Centrality、Modularity、Conductance、Graph Partitioning等。而这里我们主要关注的是Conductance,这是因为Conductance能更好地符合图聚类的直观,并且它有很好的理论保证,与图代数中的谱图理论也有较多的联系。
Problem Definition:
Conductance-based Graph Clustering
Conductance:给出一个无向图G,基于Conductance的图聚类旨在找到具有最小Conductance的顶点集C。Conductance的定义是一个比值的关系,即
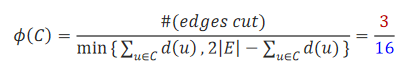
式中,分子是基于edge cut来定义的,分母的取值是顶点集C中结点度数和与补集度数和差值的最小值。我们最终的研究目的是希望Conductance的值最小,即分子最小(与外部联系最少),分母最大(C内部结点度数最多)。
Applications
Conductance也有很多应用。比较经典的应用是图像分割、社区发现、机器学习。
03
Existing Solutions
现存的基于Conductance的图聚类方法主要分为三类。第一类是基于费德勒向量(Fidler Vector)的图聚类;第二类是基于扩散的局部聚类,主要目的是得到查询结点与其余结点之间的关系,比较经典的三种方式分别是Truncated Random Walk、Personalized PageRank、Heat Kernel PageRank;第三类是除了上述两类方法以外的方式,代表性的有SDP、LP、Flow-based等。
Fiedler vector-based spectral clustering
该方法主要分为三个步骤:(1)计算归一化拉普拉斯矩阵(D-1/2(D-A)D-1/2)的第二小特征值对应的特征向量x,其中x称为费德勒向量。(2)对x中的所有项按照递增的方式进行排序,使得xv1≤xv2≤…≤xvn。(3)输出S=arg minφ(Si),其中Si={xv1,xv2,…,xvi}。
该方法的优势在于通过顺序的学习将指数的组合转化成线性的组合,缺点是第一步中计算第二小特征值的过程较慢,时间复杂度为O(n3)。
Diffusion-based local clustering
为了解决上述方法存在的问题,研究者们提出了基于扩散的局部聚类方法。该方法的主要步骤为:(1)给定一个种子节点q,它们通过一些图扩散的方式(比如:Truncated Random Walk、Personalized PageRank、Heat Kernel PageRank)计算一个概率分布π (w.r.t q),令y= π/D,其中D为对角度矩阵。(2)对y中所有非零项进行排序,使yv1≥yv2≥…≥ysup(y),其中sup(y)是y中非零项的个数。(3)输出S=arg minφ(Si),其中Si={yv1,yv2,…,yvi}。这种方式在效率上会提升很多,但是聚类质量不高。
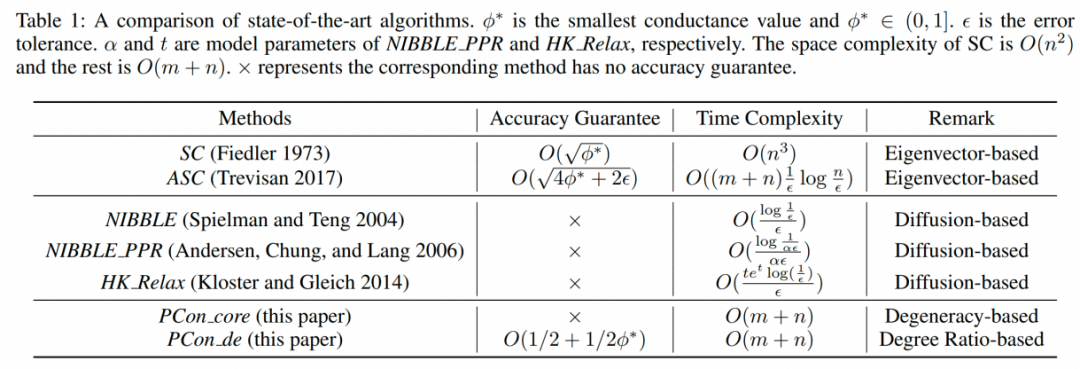
Deficiencies of Existing Solutions
该表显示了现有解决方案的不足,有两种基于特征向量的方法,即SC和ASC。有三种基于扩散的方法。从表中可以看出,基于特征向量的算法具有较高的时间和空间复杂度。基于扩散的方法没有全局Conductance保证的启发式方法。
04
Proposed Solutions: PCon_core & Pcon_de
Our Solution——Framework
由于之前工作的不足,我们提出了一个三阶段计算框架,它包含了大多数现有方法的计算范式。即现有的解决方案可以被归纳为以下三个阶段:(1)我们根据相应的应用为每个顶点给出一个预先定义的得分函数。简单来说,我们用s(u)表示顶点u的分数。(2)我们迭代地删除分数最小的顶点。这样的迭代删除过程被称为Peeling过程。(3)我们输出Peeling过程中Conductance最小的结果。但如何设计一个有效的得分函数并能有效地得到是该框架的一个重大挑战!
Degeneracy Ordering
给定一个无向图G,在G的所有顶点上的一个排列(u1,u2,…,un),如果每个顶点ui在G的子图中由ui, ui+1,…,un所构成的子图中度数最小,这样的排序称之为Degeneracy Ordering。
PCon_core
在上述框架的基础上,我们首先利用著名的Degeneracy Ordering提出了一种简单的算法PCon_core。该算法的输入为无向图,输出为聚类S。我们使用简并排序来计算出Degeneracy Ordering,并分配顶点u的分数s(u)。显然,Pcon_core具有线性的时间和空间复杂度,但在质量方面它是启发式的,没有全局的Conductance保证。

那么如何在不牺牲效率的前提下提高聚类质量?我们尝试将Conductance进行一个转换,证明在vol(S)小于m的情况下,g(S)的值最大。那么进一步能够证明最优的Conductance的顶点集的顶点有
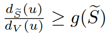
的结论,进而我们将其做出形式化的定义——度比,即u在S内部的度数与u在整个原始图度数的比值,这其实也是对顶点u赋予一个分数值。

PCon_de
于是,我们设计了一种称为PCon de的线性时间贪婪算法——PCon_de。该算法首先将当前搜索空间S初始化为V,候选结果为V,并且根据定义,每个顶点u∈S的度比为DrS(u)。随后,它在每一轮中执行贪心去除过程以提高目标簇的质量。具体来说,在每一轮中,它都会获得一个度数比最小的顶点u。第5-11行中更新当前搜索空间S、候选结果(如果有)和DrS(v)。一旦当前搜索空间为空,迭代就会终止。最后,返回作为近似解。

05
Experiments
Datasets
我们在六个现实生活中的公开数据集上评估了我们提出的解决方案,这些数据集是基于Conductance的图聚类的广泛使用的基准。实验中使用了这些数据集的最大连通分量。我们还使用五个人造图LFR、WS、PLC、ER和BA。以下六个竞争对手被实施以进行比较:基于特征向量的方法:SC和ASC;Diffusion-based methods: NIBBLE PPR、HK Relax;Flow-based methods: SimpleLocal、CRD。
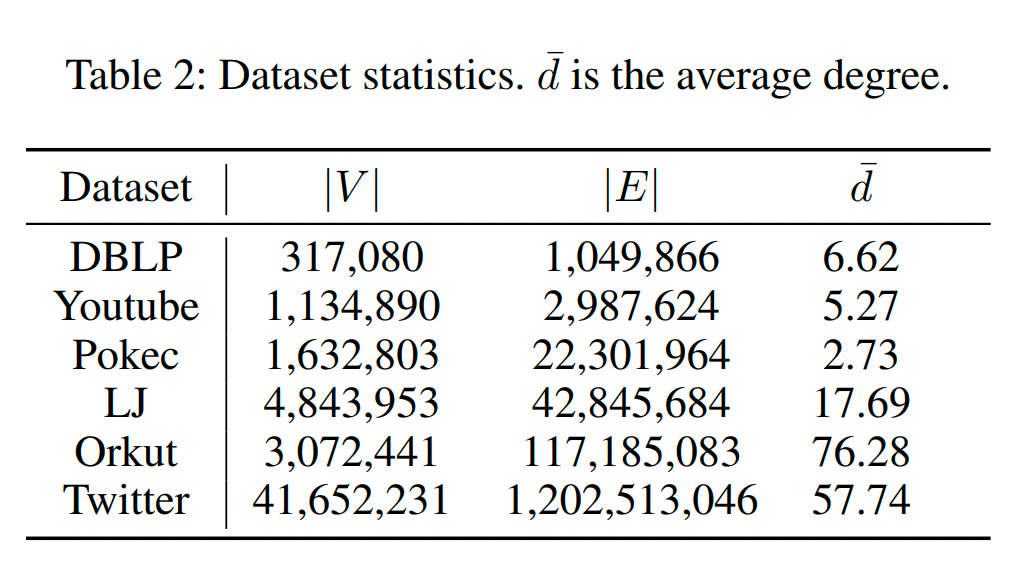
Results on real-world graphs
由下表可以看出:(1) PCon_core和P Con_de在大多数图上始终比其他方法更快,尤其是对于较大的图。特别是,它们在DBLP、Youtube、LJ和Twitter上分别实现了SC的5、14、42和17倍的加速。(2) PCon_core比PCon de稍快,但PCon_core的Conductance值较差。(3) PCon_de返回的聚类质量在六个数据集中的五个上优于其他方法。因此,这些结果清楚地表明,与基线相比,所提出的算法可以实现显著地加速和高聚类质量。
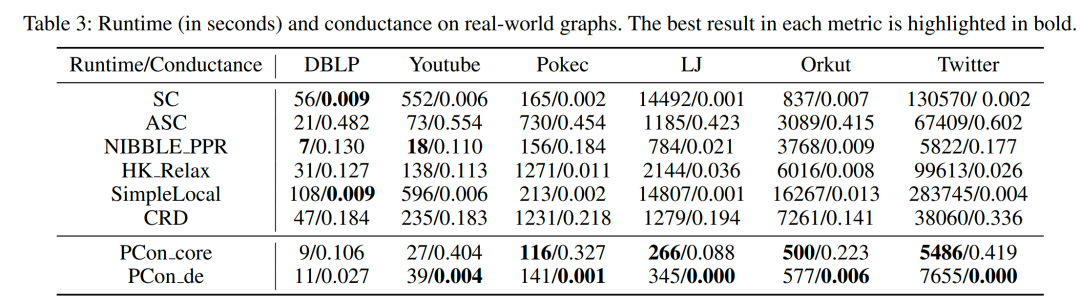
从图4中,我们可以看到PCon_core和PCon_de的内存开销在所有数据集上始终小于SC。特别地,与SC相比,它们节省了1.4∼7.8倍的内存开销。这是因为PCon_core和PCon_de只需要线性空间复杂度来计算每个顶点的分数。然而,SC采用矩阵的特征向量来计算每个顶点的得分,因此在最坏情况下需要平方空间复杂度。这些结果表明PCon_core和PCon_de的内存消耗更低。
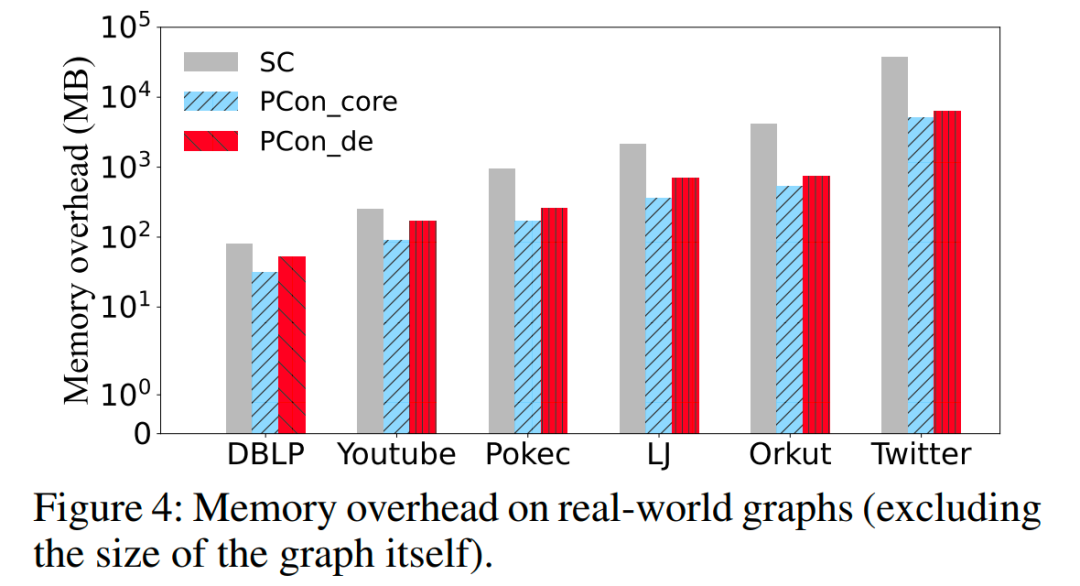
Results on synthetic graphs
我们进一步使用人造网络来评估我们提出的解决方案的可扩展性和有效性。特别地,我们只展示了图5(a)中顶点数量不同的ER的可扩展性,但所有其他合成图都有类似的趋势。可以看出,PCon_core和PCon_de 相对于图的大小接近线性。然而,SC的可扩展性较差,因为它的时间成本随着图大小的增加而波动很大。这些结果表明我们提出的算法可以处理大量图,而SC不能。
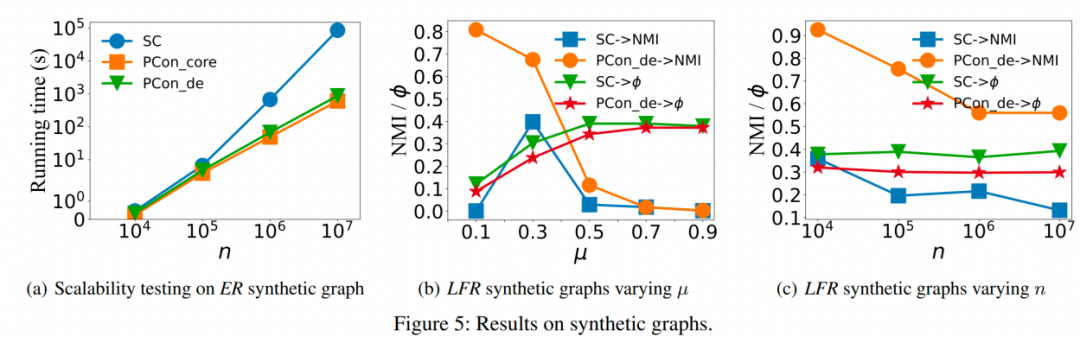
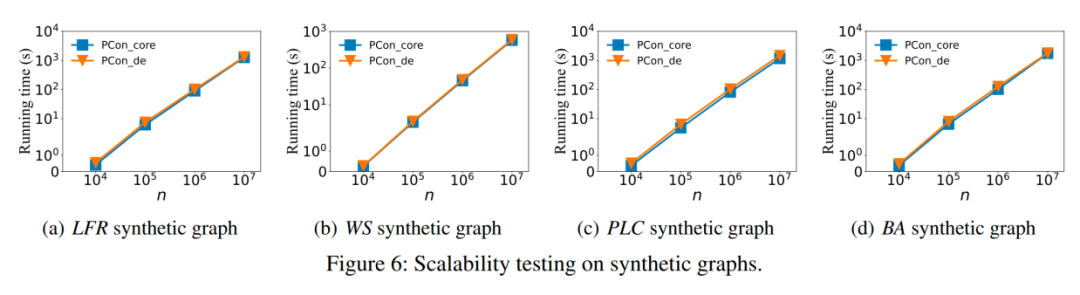
我们使用四个合成图LFR、WS、PLC和BA来评估我们提出方案的可扩展性,图6显示了结果。可以看出,PCon_core和PCon_de 相对于图的大小接近线性。因此,这些结果表明我们提出的算法可以处理大规模图。
06
Summary
(1)我们引入了PCon,这是一种新颖的基于Peeling的图聚类框架,它可以包含大多数最先进的算法。
(2)在PCon上,我们开发了两种新颖且高效的算法,具有线性时间和空间复杂度。一种是旨在优化效率的启发式算法,另一种是可以获得可证明聚类质量的近似算法。
(3)在真实和人造数据集上的结果表明,我们的算法可以在保证高聚类精度的情况下实现5~42倍的加速,而使用的内存比基线算法少1.4~7.8倍。
整理:陈研
审核:林隆龙
提
醒
点击“阅读原文”跳转可以查看回放哦!
往期精彩文章推荐

记得关注我们呀!每天都有新知识!
关于AI TIME
AI TIME源起于2019年,旨在发扬科学思辨精神,邀请各界人士对人工智能理论、算法和场景应用的本质问题进行探索,加强思想碰撞,链接全球AI学者、行业专家和爱好者,希望以辩论的形式,探讨人工智能和人类未来之间的矛盾,探索人工智能领域的未来。
迄今为止,AI TIME已经邀请了1000多位海内外讲者,举办了逾500场活动,超500万人次观看。

我知道你
在看
哦
~

点击 阅读原文 查看回放!