有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1:
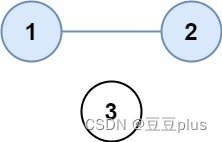
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出:2
思路:
1、我们这道题因为是要找到城市的周边,而在矩阵中第i行和第i列都表示这个城市,因此矩阵是对称的,我们只需要遍历行或者列就行。
2、假如我们先从第0行开始遍历,为了防止重复遍历,我们需要一个visited[]来判断是否已经遍历过了。同时我们还需要一个值用来记录province的数量。
3、首先找到第一个未被遍历的城市,然后进入dfs。
4、dfs中的 j 如果未被遍历同时isConnected值为1,说明和第 i 个城市连通。标记为visited
5、那与第 j 个城市连通,自然也与第 i 个城市也连通,所以继续向下遍历。
而所有递归完成后与第 i 个城市连通的所有城市都为visited,再查找到的就是新的省份了。
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
void dfs(vector<vector<int>>& graph, int i, vector<bool>& visited) {
for (int j = 0; j < graph[0] .size(); j++)
{
if (graph[i][j] == 1 /*&& i != j */&& visited[j] == false)//找到顶点i的一个未访问相邻点j
{
visited[j] = true;
dfs(graph, j, visited);
}
}
}
int findCircleNum(vector<vector<int>>& isConnected) {
int size = isConnected.size();
vector<bool> visited(size,false);//因为邻接矩阵表示无向图时候的对称性,用一维数组表示
int res = 0;
for (int i = 0; i < size; i++)
{
if (visited[i] == false)
{
visited[i] = true;
res++;
dfs(isConnected, i, visited);
}
}
return res;
}
int main() {
vector<vector<int>> graph{ {1,1,0},{1,1,0},{0,0,1} };
int res = findCircleNum(graph);
cout << res << endl;
return 0;
}