[入门必看]数据结构4.2:串的模式匹配
- 第四章 串
- 4.2 串的模式匹配
- 知识总览
- 4.2.1_朴素模式匹配算法
- 4.2.2_1_KMP算法
- 4.2.2_2_求next数组
- 4.2.3_KMP算法的进一步优化
- 4.2.1_朴素模式匹配算法
- 什么是字符串的模式匹配
- 朴素模式匹配算法
- 通过数组下标实现朴素模式匹配算法
- 代码实现:
- 4.2.2_1_KMP算法
- 优化思路 - 模式串的最后一个位置不匹配
- 优化思路 - 其他位置不匹配
- 上节例子对比
- 对例子进行改造
- KMP算法
- 利用next数组进行匹配
- 朴素模式匹配 v.s. KMP算法
- 4.2.2_2_求next数组
- 练习1:
- 手算next数组
- 使⽤next数组进⾏模式匹配
- 练习2:
- 练习3:
- 4.2.3_KMP算法的进一步优化
- 例1:第三个位置失配
- 例2:第五个位置失配
- 练习1:
- 练习2:
- 优化KMP算法
- 优化前:
- 优化后:
- 知识回顾与重要考点
- 4.2.1_朴素模式匹配算法
- 4.2.2_1_KMP算法
- 4.2.2_2_求next数组
- 4.2.3_KMP算法的进一步优化
第四章 串
小题考频:2
大题考频:0
4.2 串的模式匹配
难度:☆☆☆☆☆
知识总览
4.2.1_朴素模式匹配算法
4.2.2_1_KMP算法

4.2.2_2_求next数组
4.2.3_KMP算法的进一步优化
4.2.1_朴素模式匹配算法
什么是字符串的模式匹配
——在字符串内搜索某一段内容

查找功能

搜索引擎

- 字符串模式匹配:在主串中找到与模式串相同的⼦串,并返回其所在位置。
有可能匹配不到模式串:
子串——主串的一部分,一定存在
模式串——不一定在主串中找到
朴素模式匹配算法
——暴力解决问题
在主串中找出所有有可能与模式串相匹配的子串,并将这些子串和模式串一一进行对比











主串长度为n,模式串长度为m
朴素模式匹配算法:将主串中所有长度为m的子串依次与模式串对比,直到找到一个完全匹配的子串,或所有的子串都不匹配为止。
最多对比 n - m + 1 个子串
上一节中Index(S,T)函数的实现,采用的就是朴素模式匹配算法的思想。
1)int i=1 - 指明当前要匹配的子串是从哪个位置开始的;
2)(i<=n-m+1) - 表示最多对比n-m+1个子串;
3)SubString(sub,S,i,m); - 从主串S中,取出从位置i开始,长度为m的子串,放到sub里;
4)if(StrCompare(sub,T)!=0) ++i; - 子串和模式串对比,若不匹配,则匹配下一个子串
5)若能匹配,返回当前子串的起始位置i;
6)若都不能匹配,返回0
上述代码使用了:1)取子串的基本操作;2)对比两个字符串的基本操作
接下来:不使用字符串的基本操作,直接通过数组下标实现朴素模式匹配算法。
通过数组下标实现朴素模式匹配算法
设置两个扫描指针i和j,这两个指针指到哪就要把字符对比到哪。
Step1:
开始匹配第1个子串
对比主串和模式串的第1个字符

Step2:
如果指向的字符相等,那么让指针i和j分别后移




Step3:
到了第6个位置时,i和j所指向的字符不相等,则认为第一个子串匹配失败。

若当前⼦串匹配失败,则主串指针 i 指向下⼀个⼦串的第⼀个位置,模式串指针 j 回到模式串的第⼀个位置
i = i - j + 2
(i - j:指针指向当前子串的前一个位置;+2:指向下一个子串的起始位置)
j = 1
Step4:
第1个子串匹配失败后:
i的值回到2
j的值回到1
然后开始匹配第2个子串


匹配失败,则主串指针 i 指向下⼀个⼦串的第⼀个位置,模式串指针 j 回到模式串的第⼀个位置
Step4:
匹配下一个子串

失败,i 指向下一个子串的第一个位置,j 指向模式串第一个位置,开始匹配下一个子串。
Step5:
匹配成功!

若 j 指针大于模式串长度,j > T.length(模式串字符全部匹配成功),则当前⼦串匹配成功,返回当前⼦串第⼀个字符的位置 —— i - T.length
代码实现:

设主串⻓度为 n,模式串⻓度为 m,则
最坏时间复杂度 = O(nm)

最坏的情况,每个⼦串都要对⽐ m 个字符,共 n-m+1 个⼦串,复杂度 = O((n-m+1)m) =
O
(
n
m
)
O(nm)
O(nm)
注:很多时候,n >> m,
保留数量级更大的项,把 O ( n m − m 2 + m ) O(nm-m^2+m) O(nm−m2+m)简化为 O ( n m ) O(nm) O(nm)
4.2.2_1_KMP算法
——由D.E.Knuth,J.H.Morris和V.R.Pratt提出,因此称为KMP算法
对于朴素模式匹配算法,⼀旦发现当前这个⼦串中某个字符不匹配,就只能转⽽匹配下⼀个⼦串(从头开始)

因为我们并不知道主串里面这些字符到底是什么,所以我们必须从子串开头的第一个字符开始匹配。
如果匹配模式串时,在最后一个字符匹配失败,那么主串中之前这些字符就和模式串中的字符对应。
那么在主串中匹配失败的位置,的之前的字符,是已知的,和模式串时保持一致的。

不匹配的字符之前,一定是和模式串一致的
在朴素模式匹配算法中,匹配失败后只能从第2个子串开始重新匹配:

但是匹配第2个子串时,已知了主串中的前面这几个字符,发现刚开始就已经不匹配了,所以根本没有必要去检查和匹配。

第3个子串一样,已经知道了主串前面的几个字符,对不上,也没有必要去检查和匹配了。

匹配第4个子串时,主串里已知部分和模式串是能够匹配的,其他部分能否匹配现在还不知道,那么在这个子串中,可以从未知部分往后进行检查和匹配:

优化思路 - 模式串的最后一个位置不匹配

①不匹配的字符之前,一定是和模式串一致的;
②所以没有必要检查已知部分和模式串不匹配的子串;
③已知部分和模式串相匹配的子串中,已经匹配的部分(已知部分)也不用再次对比;
④直接从【已知部分和模式串相匹配的子串】的未知部分开始匹配。

跳过了中间几个子串的对比,也调过了当前子串已知的部分的对比,提高了算法效率
对于模式串 T = ‘abaabc’,当第6个元素匹配失败时,可令主串指针 i 不变(指向当前失配的字符),模式串指针 j=3(从模式串的第3个字符向后依次匹配)
得到的结论只和模式串有关,与匹配到主串的哪个位置没有关系。
验证(从第5个位置开始匹配):

匹配到当前子串的最后一个字符时,字符失配。
那么前面的字符就和模式串保持一致,即已知部分。

使用之前的结论:
对于模式串 T = ‘abaabc’,当第6个元素匹配失败时,可令主串指针 i 不变(指向当前失配的字符),模式串指针 j=3(从模式串的第3个字符向后依次匹配)

验证了该结论对模式串’abaabc’具有通⽤性,和主串没有半⽑钱关系。
以上是对于模式串T = ’abaabc’的第6个元素匹配失败的情况。
优化思路 - 其他位置不匹配
考虑其他位置的情况。
对于模式串 T = ‘abaabc’,当第5个元素匹配失败时? 怎么搞?
- 第5个元素匹配失败,可以知道主串中前面4个元素的信息,与模式串保持一致

第2个子串也不能匹配上:

第3个子串也不能匹配上:

第4个子串可以匹配上:

此时可令主串指针i不变,模式串指针j = 2
从模式串的第二个元素开始匹配即可
- 第4个元素匹配失败,可以知道主串中前面3个元素的信息,与模式串保持一致

第2个子串不能匹配上:

第3个子串可以匹配上:

此时可令主串指针i不变,模式串指针j = 2
从模式串的第二个元素开始匹配即可
- 第3个元素匹配失败,可以知道主串中前面2个元素的信息,与模式串保持一致

第2个子串不能匹配上:

所以从第3个子串开始重新匹配:

此时可令主串指针i不变,模式串指针j = 1
从模式串的第一个元素开始匹配即可
- 第2个元素匹配失败,可以知道主串中前面1个元素的信息,与模式串保持一致

所以从第2个子串开始重新匹配:

此时可令主串指针i不变,模式串指针j = 1
从模式串的第一个元素开始匹配即可
- 第1个元素匹配失败,只能尝试匹配下一个子串:

尝试匹配下一个子串:

结论:
对于模式串 T = ‘abaabc’
当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
上节例子对比

第六个字符匹配失败:

如果用朴素模式匹配算法:

朴素模式匹配算法,此时应令i = i - j + 3,j = 1;
如果用优化思路:

当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++

优化之后,主串指针不需要回溯。
采用这种策略,效率大幅度提高。
对例子进行改造
第5个元素改成c:

第5个元素发生失配:

优化思路:

当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
此时第2个元素仍匹配失败:

当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
此时第1个元素仍匹配失败:

当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++

此时第1个元素匹配,第2个元素匹配失败:

当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++

此时第3个元素匹配失败:

当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
此时第1个元素匹配失败:

当第6个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=3
当#pic_center第5个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第4个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=2
当第3个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第2个元素匹配失败时,可令主串指针 i 不变,模式串指针 j=1
当第1个元素匹配失败时,匹配下⼀个相邻⼦串,令 j=0, i++, j++
最终因为指针j超出模式串的范围而停止:

完成匹配工作。
整个过程中i不用回溯。
怎么⽤代码实现这个处理逻辑?
对于模式串T = ‘abaabc’
用数组来表示模式串指针需要修改的信息

特别地,第1个元素失配时,要将j = 0 再让 i++, j++
if (S[i] != T[j]) //模式串在第几个位置失配时,使用第几个位置的指针修改信息
j = next[j];
if(j == 0) {i++; j++} //第1个位置时,匹配下一个相邻子串
KMP算法
是的,这就是KMP算法。

KMP算法的整体流程就是在进行模式匹配之前,需要先进行一个预处理:
- 分析模式串,求出和模式串相对应的这个next数组。
- 然后再利用next数组来进行模式匹配,整个匹配的过程主串的指针i是不需要回溯的。
利用next数组进行匹配

传入主串的值S、模式串的值T、和模式串相对应的这个next数组;
从主串的1和模式串的1位置开始往后匹配;
如果,主串的当前元素和模式串的当前元素相等的话,即匹配成功,i和j同时++;
并且当j == 0时,也需要让i和j同时++
否则,说明i和j所指元素不匹配,失配时让j = next[j]即可。
朴素模式匹配 v.s. KMP算法

对比发现,其实修改的部分即黄色框所框出部分,和需要传入一个next数组。
有了next数组后,当主串和模式串发生失配时,不需要再修改主串的指针i让其回溯,只需要修改模式串的j指针即可。
朴素模式匹配算法,最坏的时间复杂度
O
(
m
n
)
O(mn)
O(mn)
KMP算法,最坏的时间复杂度
O
(
m
+
n
)
O(m+n)
O(m+n)
其中,求 next 数组时间复杂度 O(m)
模式匹配过程最坏时间复杂度 O(n)
需要掌握手算next数组的方法。
4.2.2_2_求next数组
——(⼿算练习)
next数组的作⽤:当模式串的第 j 个字符失配时,从模式串的第 next[j] 继续往后匹配
练习1:
手算next数组
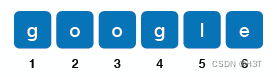 的next数组:
的next数组:

next数组的下标与字符串的下标一一对应,1~6。
- next[1]:
【当模式串的第一个字符匹配失败时,模式串指针j应该指向什么位置】

当第一个字符匹配失败时,直接让i++,j++,即开始匹配后一个子串和模式串:

该逻辑对于任何一个模式串都是一样的,只要第1个字符发生了不匹配的情况,只能让他匹配下一个子串。
所以所有的模式串next[1]肯定都是0。
- next[2]:
【当模式串的第二个字符匹配失败时,模式串指针j应该指向什么位置】

此时,只能让模式串往后滑动一位,即指向1位置:

该逻辑对于任何一个模式串都是一样的,只要第2个字符发生了不匹配的情况,应尝试匹配模式串的第1个字符。
所以所有的模式串next[2]肯定都是1。
- next[3]:
【当模式串的第三个字符匹配失败时,模式串指针j应该指向什么位置】

在不匹配的位置前划出分界线,左边的部分是已知的,右边是未知的。
尝试让模式串一步一步往右移,过程中,观察分界线左边部分能否匹配上。
直到分界线之前“能对上”,或模式串完全跨过分界线为止。
此时j指向哪儿,next数组值就是多少。
往右移动一步:
发现分界线左边的g和o失配,说明模式串右移一步不够。
继续往右移动一步:

此时整个模式串跨过了分界线,此时要继续向后检查模式串的j和右边位置未知元素i是否匹配。
此时j的值为1,那么next[3] = 1
- next[4]:
【当模式串的第四个字符匹配失败时,模式串指针j应该指向什么位置】

Step1:分界线

分界线左边的值是可以确定的,逐步向右移动模式串看是否匹配,或者模式串跨过分界线。
Step2:右移一步

失配。
Step3:右移两步

失配。
Step4:右移三步

此时模式串跨过分界线,j指向1,next[4] = 1
- next[5]:
【当模式串的第五个字符匹配失败时,模式串指针j应该指向什么位置】

重复以上步骤,逐步向右移动模式串,找匹配部分。
最终找到了分界线左边的匹配部分,接下来检查右边i和j是否匹配:

此时j指向2,next[5] = 2
- next[6]:
【当模式串的第六个字符匹配失败时,模式串指针j应该指向什么位置】

重复以上步骤,逐步向右移动模式串,找匹配部分。
最终模式串跨过分界线,之后需要检查i和模式串第1个字符能否匹配:

此时j指向1,next[6] = 1
使⽤next数组进⾏模式匹配
给出主串S为googlo goo google,在其中找到模式串google:

已经手算得到next数组:

开始进行模式匹配
Step1:第6个元素匹配失败

j = 6 时失配,此时让 j = next[j],即 j = next[6],
接下来让 j = 1

Step2:第1个元素匹配失败
j = 1 时失配,此时让 j = next[j],即 j = next[1],
接下来让 j = 0

j = 0时让i和j都++

Step3:第5个元素匹配失败

j = 5 时失配,此时让 j = next[j],即 j = next[5],
接下来让 j = 2

Step4:匹配成功

练习2:
求模式串T = ababaa的next数组
模式串长度是6,next组数有next[1]~next[6]
总结规则:

Step1:next[1]=0和next[2]=1

Step2:求next[3]

模式串跨过分界线,此时j = 1,next[3] = 1
Step3:求next[4]
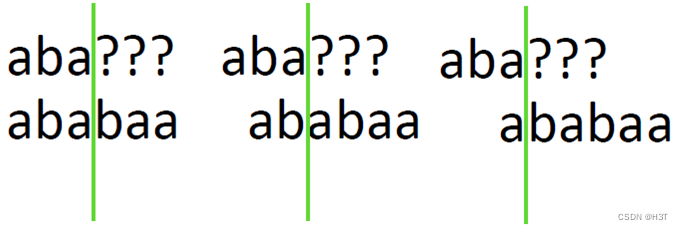
分界线左边匹配成功,此时j = 2,next[4] = 2
Step4:求next[5]

分界线左边匹配成功,此时j = 3,next[5] = 3
Step5:求next[6]

分界线左边匹配成功,此时j = 4,next[6] = 4
练习3:


求next数组:

4.2.3_KMP算法的进一步优化
——求nextval数组
KMP算法优化的思路:
以之前小节中的模式串abaabc为例,已经求出了这个模式串的next数组。

模式串abaabc的next数组:

例1:第三个位置失配
如果第三个位置发生失配时,让j指针指回next[3]

此时说明主串中第三个字符和模式串的第三个字符a是肯定不相等的。
即主串中第三个字符肯定不是a。

如果此时按照next数组中 next[3] = 1,来进行匹配,那么这一次匹配也一定是失败的。
next[3] = 1,来进行匹配,那么这一次匹配也一定是失败的。
因为模式串中的第一个字符为a,而且已经知道了主串中的第三个字符不为a
这次匹配失败后,那么应该让j指针等于next[j],也就是等于0。
所以当第3个字符匹配失败的时候,让j = 0,即next[3] = 0。
优化后:

第3个位置失配时:

直接让j = next[3] = 0

那么下一个匹配的位置就会直接跳过这个字符,因为会让i和j同时++

例2:第五个位置失配
假设模式串在第5个位置失配,那么KMP算法会让j = next[5] = 2。

虽然暂时不知道主串i指针所指位置的字符是什么,但是肯定不是b。

所以如果按照刚才让j指针指向2位置,接下来的这次匹配一定是失败的,因为字符2和字符5都是b,然后还需要让j = next[2] = 1。
所以干脆就一步到位,让next[5] =next[2]的值:
即j = next[5] = 1:
此时回到上面的情况,如果字符5发生失配,j = next[5],直接就j = 1,节约了一个步骤,没有必要再让next[5] = 2,即比较第二个字符,因为肯定匹配不上。
这就是优化。
当然不是所有next数组都可以优化,优化思路为:
需要判断next数组所指的字符和原本失配的字符是否相等。
- 如果这两个字符不相等,那么next数组保持不变;
- 如果这两个字符相等,那么next数组就可以进行优化。

将next数组优化成nextval,然后再KMP算法匹配的时候,用nextval数组替代next数组,其他一样。
练习1:
对于这个模式串:

求出其next数组:

然后手算其nextval数组:

首先,nextval[1]的值直接写=0;
然后,如果当前的next[j]所指字符,和目前j所指的字符不相等,就让nextval的值等于next的值,所以nextval[2]应该等于1。
- 如,next[2] = 1,所指字符为第1个,即a,和目前j所指的第2个字符b不相等,那么nextval[1] = next[1] = 1

- 如,next[3] = 1,所指字符为第1个,即a,但是目前j所指第3个字符为a相等,那么就让nextval[3] = nextval[next[3]] = nextval[1] = 0,即跳到1对比失败的那个next,即next[1] = 0。
也就是说直接把next[3]的值优化为next[1]的值,即0。

同样的,第四个字符b失配时,next[4] = 2,跳到第二个字符b时相等,那么
nextval[4] = nextval[next[4]] = nextval[2] = 1

第五个字符a失配时,next[5] = 3,跳到第三个字符a时相等,那么
nextval[5] = nextval[next[5]] = nexvalt[3] = 0
第六个字符a失配时,next[6] = 4,跳到第四个字符b时不相等,那么
nextval[6] = next[6] = 4

最终求出了nextval数组:

练习2:
对于模式串:

其next数组是:

nextval[1] = 0;
第二个字符和next[2]所指字符相等,nextval[2] = nextval[next[2]] = 0;
第三个字符和next[3]所指字符相等,nextval[3] = nextval[next[3]] = 0;
第四个字符和next[4]所指字符相等,nextval[4] = nextval[next[4]] = 0;
第五个字符和next[5]所指字符不相等,nextval[5] = [next[5] = 4。
所以求得其nextval数组为:

优化KMP算法
——感受一下优化的力量
优化前:

此时匹配到第4个字符,失配。到next[4] = 3:

此时第3个字符依然失配。到next[3] = 2:

此时第2个字符依然失配。到next[2] = 1:

此时第1个字符依然失配。到next[1] = 0:

j = 0时,i和j同时++:

此时匹配成功:

优化后:

此时匹配到第4个字符,失配。到nextval[4] = 0:

j = 0时,i和j同时++:

此时就跳过了刚才中间部分的对比。
接下来匹配成功:

把next数组优化为nextval数组之后,中间减少了很多没有必要的对比。
知识回顾与重要考点
4.2.1_朴素模式匹配算法

- 暴力解法:把所有有可能的子串遍历一遍
- 最坏时间复杂度 =
O
(
n
m
)
O(nm)
O(nm)
——每一个子串前面所有元素都和模式串匹配,只有最后一个元素和模式串不匹配
4.2.2_1_KMP算法
- 需要掌握手算next数组的方法
- 记住KMP算法的整体时间复杂度
O
(
m
+
n
)
O(m+n)
O(m+n)
——预处理(next数组)时间复杂度 O ( m ) O(m) O(m);模式匹配时间复杂度 O ( n ) O(n) O(n)
4.2.2_2_求next数组

4.2.3_KMP算法的进一步优化

- 串在考试中的地位










![[LeetCode]路径总和](https://img-blog.csdnimg.cn/img_convert/2f6a8595f9e62ffaf3ea755b79e8e2ec.jpeg)



![C++ 高级数据结构————[ 单调栈 ]](https://img-blog.csdnimg.cn/bf408ca26f2546938f237f948fe2b61e.png)