每周一篇的算法文章来了
今天讲解的是高级数据结构中的——单调栈
单调栈,顾名思义,就是升级版的栈()
先回顾一下栈把
栈,是一种线性表,它的特点是只能从一边进出,并且先进后出,后进先出。就想枪的弹夹一样。
而单调栈,跟他有一点不同
单调栈,每时每刻都要保持栈中呈现单调递增或单调递减
但是,有一个问题:
还是举个栗子
如果把6,7,12,3,1,8依次入栈,那么就会呈现这种样子
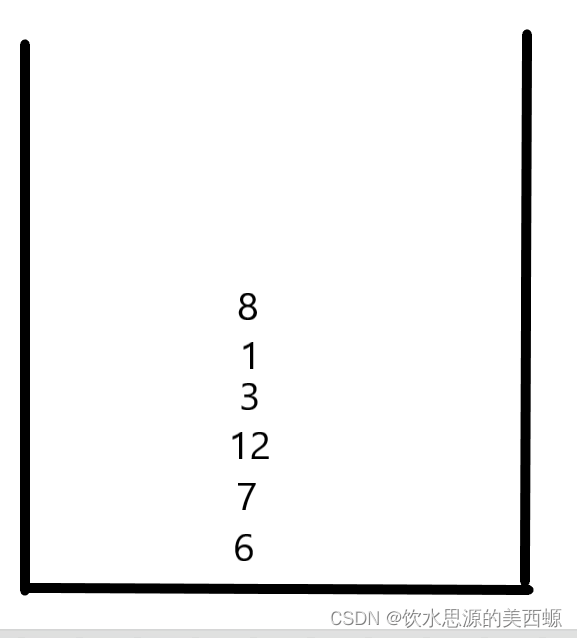
怎么看,他都不是单调递增或递减
那我们就要引入单调栈的方法了
一.单调递增栈
单调递增栈中的单调递增,指的是依次出栈的数据呈单调递增
就比如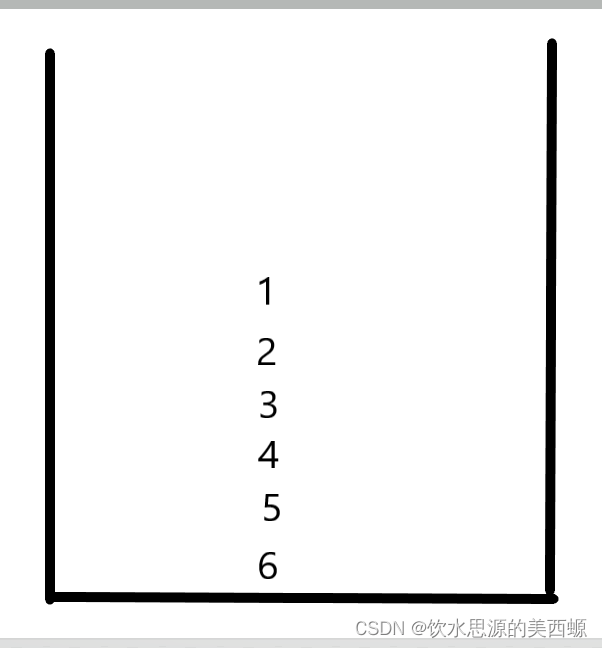
在出栈时,顺序为1,2,3,4,5,6
回到刚才的栗子

如果要达到单调递增栈
顺序就是这样的:
首先,6入栈
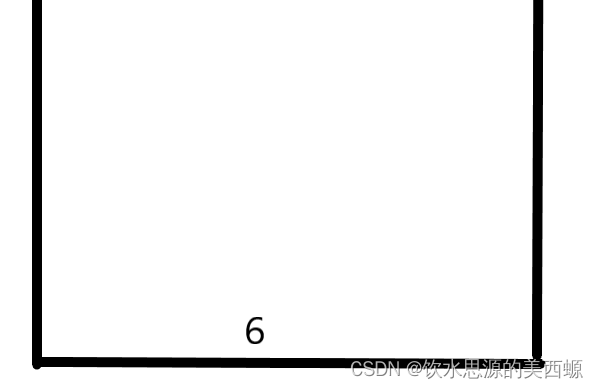
接着,7如果入栈,就不满足单调递增,所以要把6踢了,让7入栈
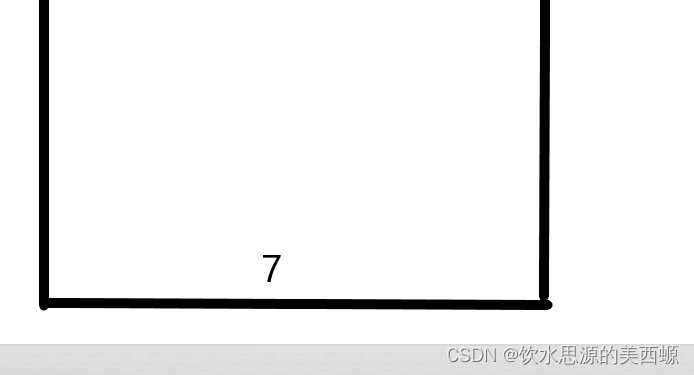
然后12要入栈,把7踢了,保证单调性
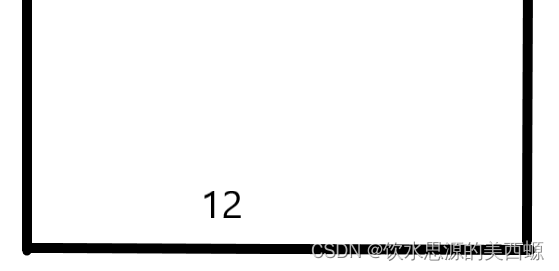
接着,3正常入栈,能够保持单调递增
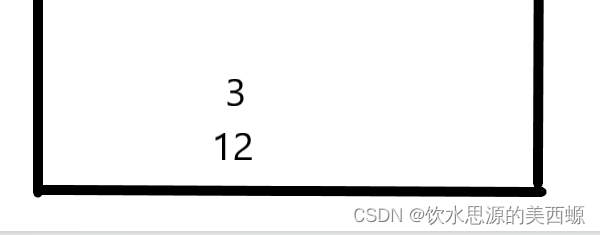
1也正常入栈
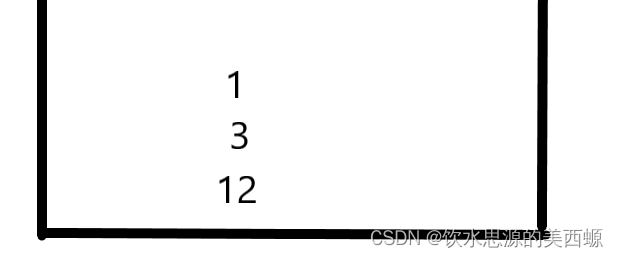
因为8要入栈,所以为了保持单调性,必须把1和3踢了

最后的单调递增栈的样子
代码:
单调递增栈:找到右起第一个比当前数字大的元素
for (int i=T.size()-1;i>=0;i--){
while(!st.empty()&&T[st.top()]<=T[i]){
st.pop();
}
st.push(i);
}二.单调递减栈
与单调递增栈相反,单调递减栈是按照出栈顺序来说从大到小
还是模拟一遍栗子:
首先6照常进栈
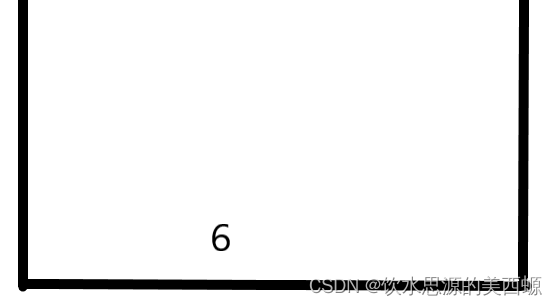
7也是照常进栈,并且能保持单调递减性
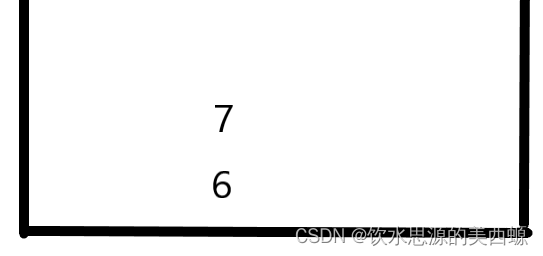
12也照常进栈
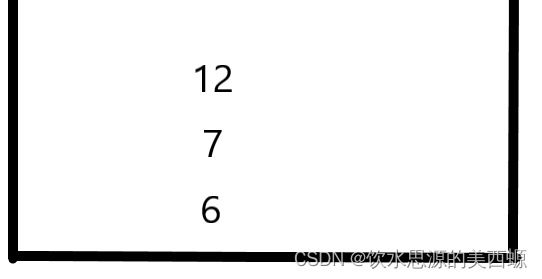
这时,3要进栈,为了保持单调性,必须把比他大的都踢出去,也就是所有
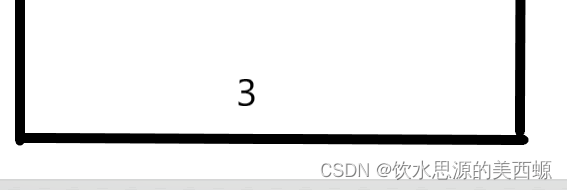
因为1要进栈,并且保持单调性,所以踢了3
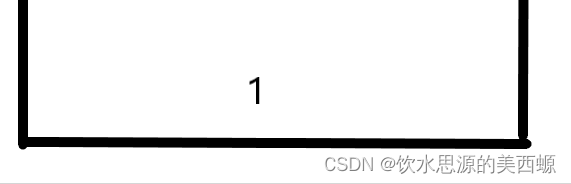
最后8照常进栈

整个的单调递减栈就是这样的
代码:
找出左起第一个小于等于当前数字的元素
for (int i=0;i<T.size();i++){
while(!st.empty()&&T[st.top]>T[i]){
st.pop();
}
st.push(i);
}作用:
单调栈可以以O(n)的时间复杂度求出某个数的左边第一个比他小于的或右边第一个比他大于的
例题:
题目描述
给出项数为n的整数数列a1…n。定义函数 f(i) 代表数列中第 i个元素之后第一个大于 ai 的元素的下标,即 f(i)=mini<j<=n, aj>ai{j}。若不存在,则f(i)=0,试求出 f(1…n) 。
输入
第一行一个正整数n,第二行n个正整数 a1…n。
输出
一行n个整数f(1…n)的值。
样例输入1
5
1 4 2 3 5
样例输出1
2 5 4 5 0单调递增栈的模板题
# include <iostream>
# include <cstdio>
# include <algorithm>
# include <stack>
using namespace std;
# define int long long
int n,a[3000005],f[3000005];
stack <int> s;
signed main(){
scanf("%lld",&n);
for (int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
for (int i=n;i>=1;i--){
while(!s.empty()&&a[s.top()]<=a[i]){
s.pop();
}
f[i]=s.empty()?0:s.top();
s.push(i);
}
for (int i=1;i<=n;i++){
printf("%lld ",f[i]);
}
return 0;
}
---------------------------------------------------------------------------------------------------------------------------------
今天对单调栈的讲解就到这里
有什么问题大家可以随时评论区讨论