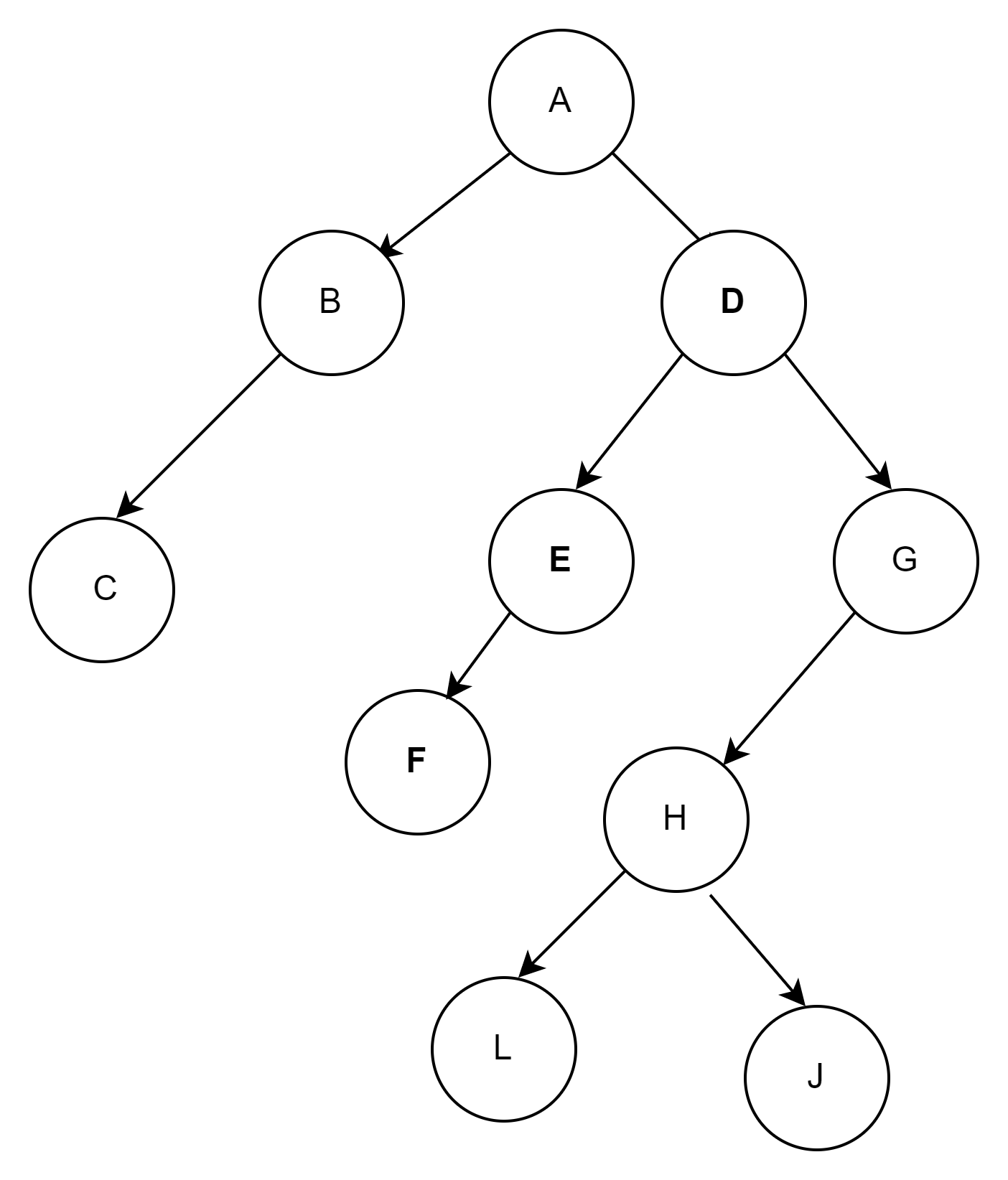
一：给图求前序，中序，后序

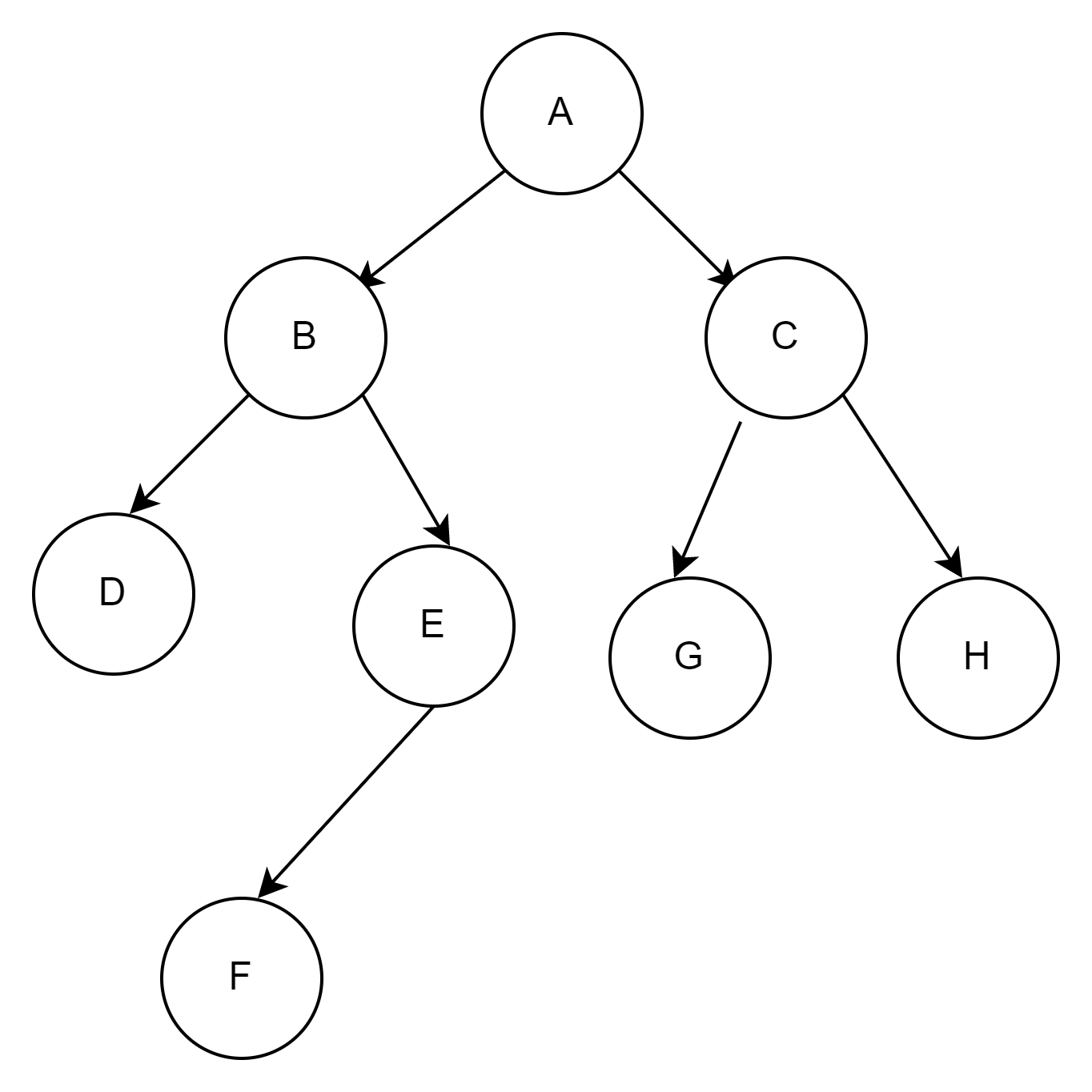
前序遍历（先序遍历）

核心思想：根左右

前序序列：ABDEFCGH

先访问根结点A，打印A，然后访问左子树，此时左子树B又作为根节点，打印B

再访问B的左子树D，打印D，再访问B的右子树E，打印E，此时E又是根结点

再访问E的左子树F，此时A的左子树已访问完毕。然后继续访问A的右子树，方法相同

（根左右）。

中序遍历

核心思想：左根右

中序序列：DBFEAGCH

先访问A结点的左子树B，B结点有左子树D，所以先访问D结点，打印D结点，

根据（左根右）思想访问根结点B，打印B，再访问E结点，E结点有左子树F，

所以先访问F，访问完F结点后再访问E结点，打印E结点，访问E结点后，则A结点

的左子树访问完毕，再访问A结点，打印A结点。

访问完A的左子树，根据同样的方法访问A的右子树。

后序遍历

核心思想：左右根

后序序列：DFEBGHCA

先访问A结点的左子树B，左子树B又是根结点，并且B结点有左子树D，打印D，

再访问E结点，E结点有左子树F，所以先访问F结点，访问完F结点后再访问根

结点E，然后访问B结点，打印B结点；访问完B结点后，再访问A的右子树部分，

结点C有左子树G，所以先访问G，打印G，然后访问H结点，打印H结点，接着访问

C结点打印C结点，最后再访问A结点，打印A结点。

二，给序列画图

已知前序序列，中序序列，求后序列并画出图

前序序列：A B C D E F G H L J

中序序列：C B A F E D L H J G

根据前序序列，可知该序列的根结点为A，根据中序序列的（左根右）思想，

可知C B为A的左子树，F E D L H J G为A的右子树

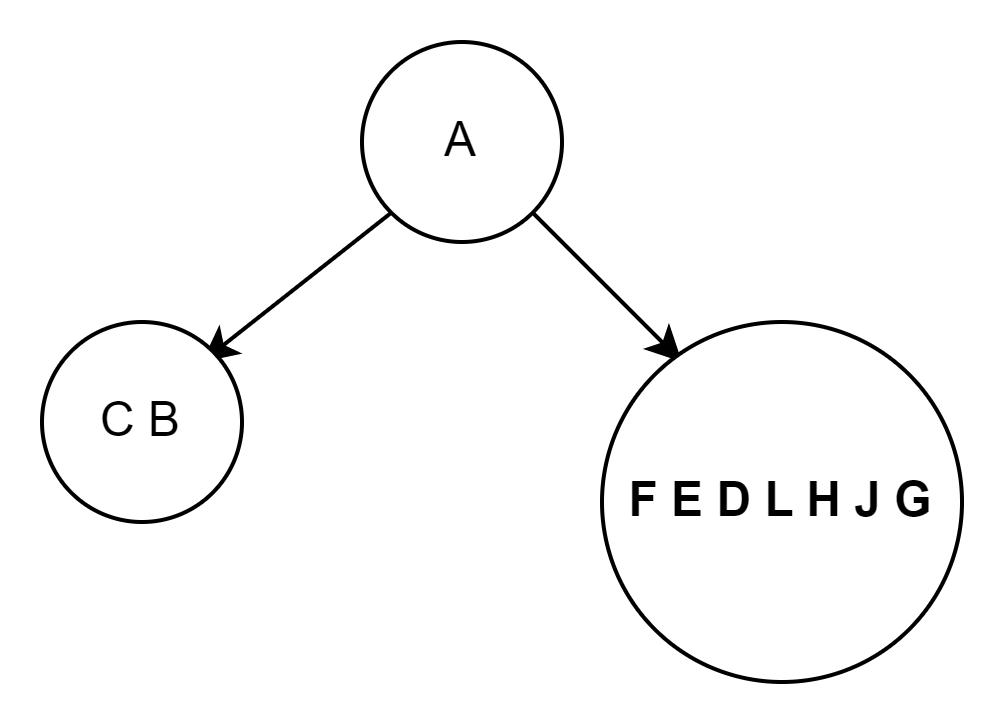
中序C B根据（左根右）可知C为B的左子树

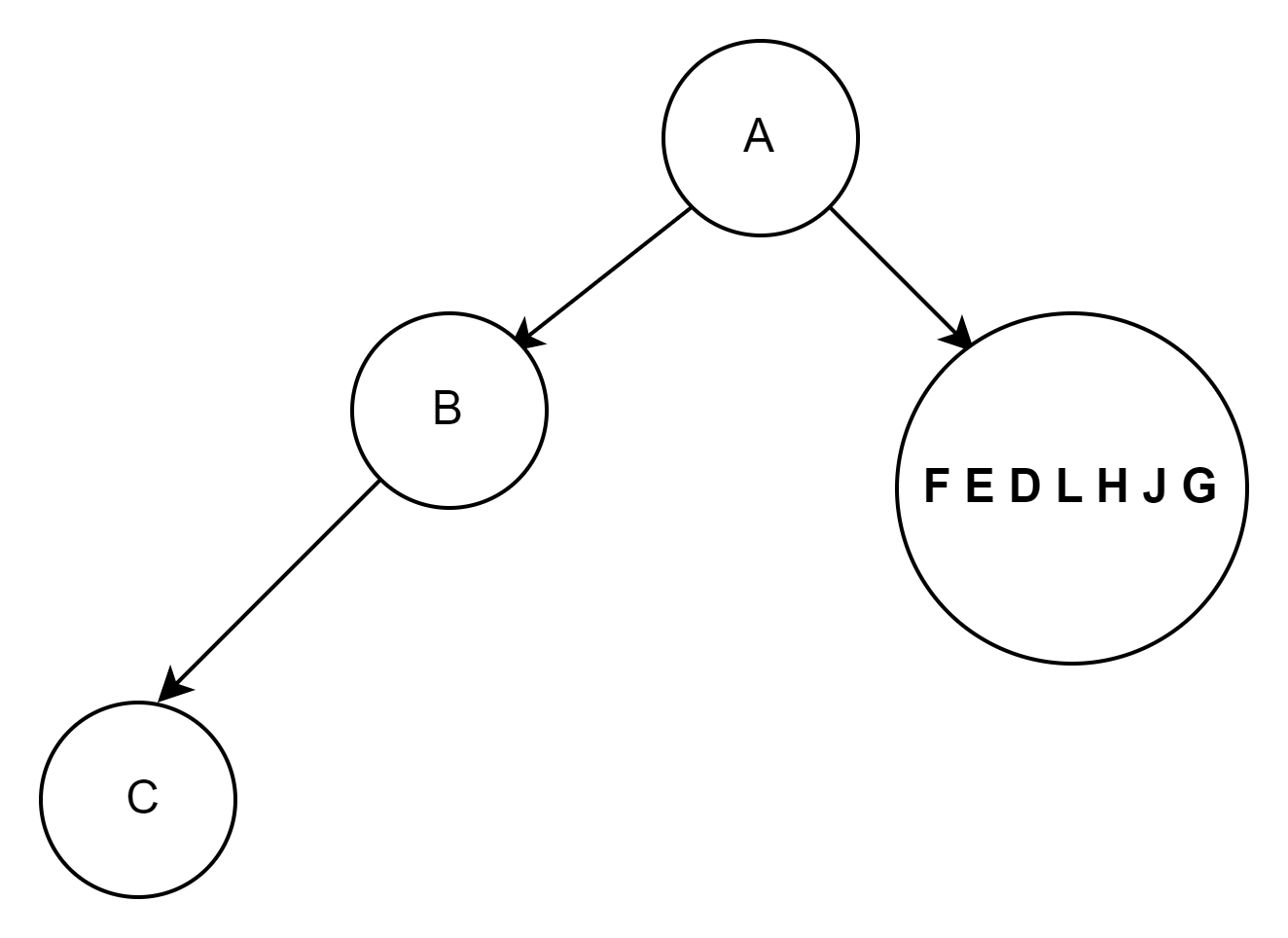
前序：D E F G H L J

中序：F E D L H J G

根据前序根左右，可知D为（EFGHIJ）的结点

根据中序左根右 ，可知F E为D的左子树，L H J G为D的右子树

      

前序：E F

中序：F E

根据前序（根左右） 中序（左根右）可知E 为结点，F为E的左子树

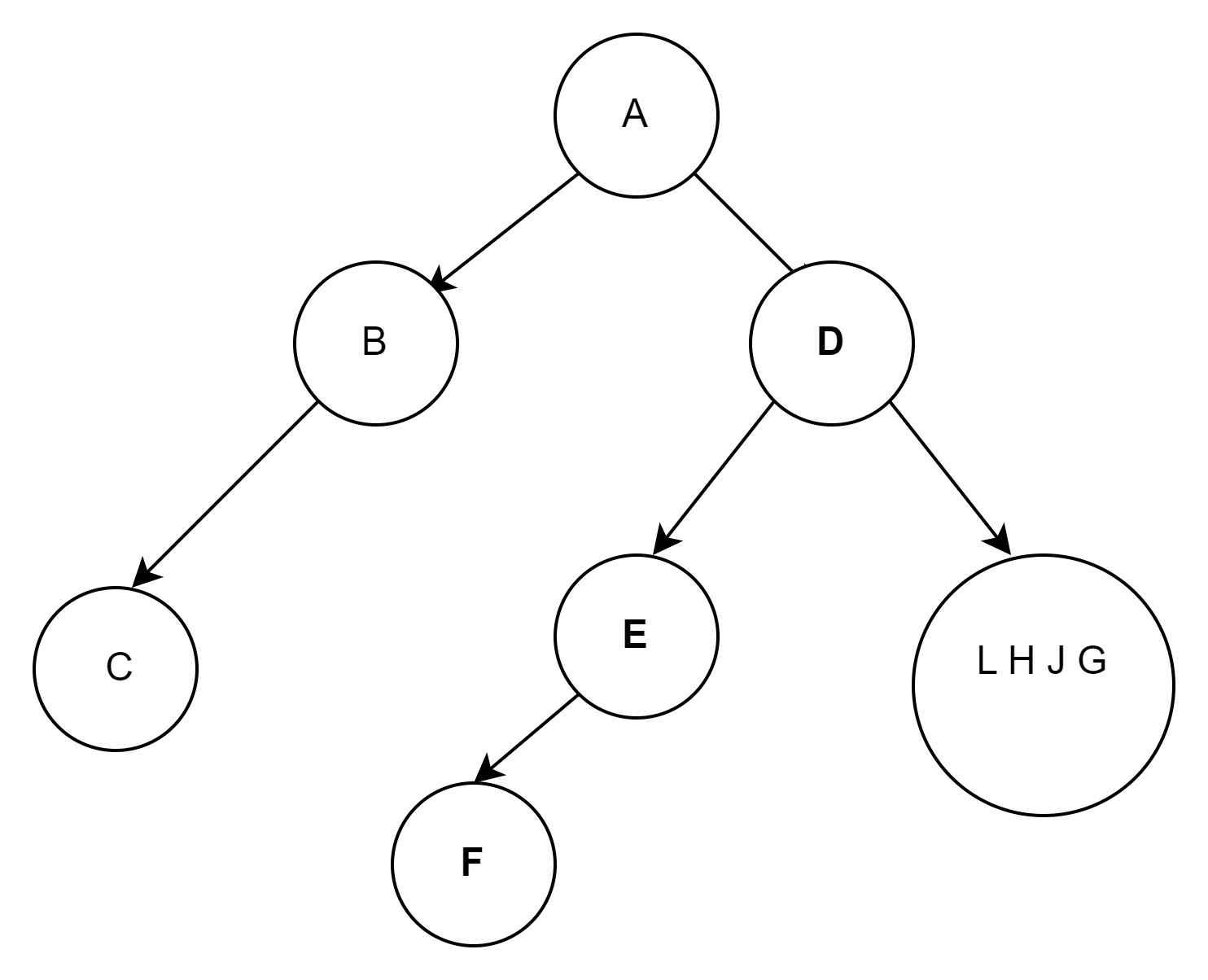
前序：G H L J

中序：L H J G

 根据前序（根左右）可知G为根结点，根据中序（左根右)可知L H J为G的左子树

前序:H L J

中序：L H J

 根据前序（根左右）可知H为根结点，根据中序（左根右)可知L为H的左子树

J为H的右子树