题目描述

建立一个类Equation，表达方程ax2+bx+c=0。类中至少包含以下方法：

1、无参构造（abc默认值为1.0、1.0、0）与有参构造函数，用于初始化a、b、c的值；

2、set方法，用于修改a、b、c的值

3、getRoot方法，求出方程的根。

一元二次方程的求根公式如下：

 

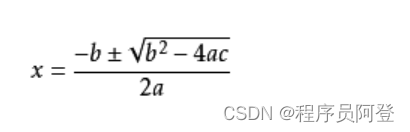
一元二次方程的求解分三种情况，如下：

输入

输入测试数据的组数t

第一组a、b、c

第二组a、b、c

输出

输出方程的根，结果到小数点后2位

在C++中，输出指定精度的参考代码如下：

#include <iostream>

#include <iomanip> //必须包含这个头文件

using namespace std;

void main( )

{ double a =3.14;

  cout<<fixed<<setprecision(3)<<a<<endl;  //输出小数点后3位

｝

---

输入样例

3
2 4 2
2 2 2
2 8 2
 

---

输出样例

x1=x2=-1.00
x1=-0.50+0.87i x2=-0.50-0.87i
x1=-0.27 x2=-3.73
 

---

 

 

#include <iostream>
#include <iomanip> //必须包含这个头文件
#include <math.h>
using namespace std;

class Eq
{
private:
	double a, b, c, x1, x2;
public:
	Eq() { a = 1; b = 1; c = 0; x1 = x2 = 0; };//初始
	void set(double x, double y, double z);//赋值
	void getRoot();//求根
};

//赋值
void Eq::set(double x, double y, double z)
{

	a = x; b = y; c = z;
	//cout << a << b << c <<"        1" << endl;
}





//Δ＝b＾2－4ac≥0时，x＝［－b±（b＾2－4ac）＾（1／2）］／2a。当Δ＝b＾2－4ac＜0时，x＝｛－b±［（4ac－b＾2）＾（1／2）］i｝／2a。
//求根
void Eq::getRoot() {
	double derta;
	derta = b * b - 4 * a * c;
	if (derta > 0)
	{
		x1 = ((-b) + sqrt(derta)) / (2 * a);
		x2 = ((-b) - sqrt(derta)) / (2 * a);
		cout << "x1=" << fixed << setprecision(2) << x1
			<< " x2=" << fixed << setprecision(2) << x2 << endl;
	}
	if (derta == 0)
	{
		x1 = ((-b) + sqrt(derta)) / (2 * a);

		cout << "x1=x2=" << fixed << setprecision(2) << x1 << endl;
	}
	if (derta < 0)
	{
		double i1;
		x1 = (-b) / (2 * a);
		i1 = sqrt(-derta) / (2 * a);
		cout << "x1=" << fixed << setprecision(2) << x1 << "+" << fixed << setprecision(2) << i1 << "i "
			<< "x2=" << fixed << setprecision(2) << x1 << "-" << fixed << setprecision(2) << i1 << 'i' << endl;
	}
}

int main()
{
	int t;
	cin >> t;

	for (int i = 0; i < t; i++)
	{
		Eq* a = new Eq[t];//动态数组
		double x, y, z;
		cin >> x >> y >> z;
		a[i].set(x, y, z);//传入数字进去
		a[i].getRoot();
	}
}