Faster Dynamic Graph CNN: Faster Deep Learning on 3D Point Cloud Data | IEEE Journals & Magazine | IEEE Xplore
题目:Faster Dynamic Graph CNN: Faster Deep Learning on 3D Point Cloud Data(更快的动态图形CNN:对3D点云数据进行更快的深度学习)
Abstract
由于卷积神经网络(CNN)或递归神经网络(RNN)的非结构化和无序特征,很难将点云数据作为输入应用于卷积神经网络(CNN)。在这项研究中,这个问题是通过图CNN在规范空间中排列点云数据来解决的。所提出的图形CNN在网络的每一层动态工作,并通过捕获点的相邻信息来学习全局几何特征。此外,通过使用squeeze-and-excitation module(挤压激励模块)重新校准每层的信息,我们在性能和计算成本之间实现了良好的权衡,并设计了residual-type skip connection network(残差型跳过连接网络)来有效地训练深度模型。使用所提出的模型,我们在基准数据集(即ModelNet40和ShapeNet)的分类和分割方面实现了最先进的性能,同时能够比其他类似模型快2到2.5倍的模型训练。
I.Introduction
本研究的主要贡献如下:
-
使用边缘卷积块上的重校准块可以提高边缘特征和点特征图的表达能力。
-
使用跳跃密集网络,我们更快地学习了具有更多层数的模型。
-
对所提出的模型进行实验,并在基准数据集上实现了最先进的性能,学习速度比其他类似模型快 2 到 2.5 倍。
II. Related Works
A. Deep Neural Network Architectures 深度神经网络架构
- VGGNet [21] 和inception model(初始模型) [14] 可以在神经网络模型中提供改进的深度。
- Batch normalization(批量归一化) [13] 可以通过插入模块来调整层输入来稳定学习过程。
- ResNet [22], [23] 可以使用跳过连接有效地学习高深度模型
- highway network(高速公路网络) [24] 可以使用门控机制调整短连接。
- [25],[26]的作者通过改革网络之间的连接进一步改进了学习特征。
- 参考文献 [27], [28] 提出了分组卷积,通过增加变换的基数来提高性能。
- 参考文献[14],[29],[30]提出了广义分组卷积概念 - 多分支收敛 - 实现了更灵活的算子配置。
- 参考文献[31],[32]提出了一种自动化的学习方法,并表现出有竞争力的表现。
- 参考文献 [33]、[34] 展示了映射到新的特征组合的跨通道相关性
- 参考文献 [35] 提出了使用标准卷积滤波器的跨通道相关性 1×1 卷 积。
其他研究已经进行了以使用“注意力”来提高模型的性能,这可以被描述为权重重要性的向量。
- 注意标识输入元素与其他元素的关联程度,并通过它们的总和来表示它们,以预测或估计任何输入元素
- 注意力通常通过门控功能(如softmax或sigmoid)或顺序技术来实现[39]。
- 作者在[41]中引入了使用沙漏模块[16]的强大干线和掩模连接机制,以及插入中间级之间的深度残差网络中的高容量单元,表现出优异的性能。
- SE网络(SE-net)[18]专注于通道关系,使用重新校准通道功能的模块,在ImageNet识别方面实现了最先进的结果。
在本文中,我们提出了一种以3D点云数据为输入的DNN。与现有的3D深度学习模型相比,我们的模型使用跳过连接网络和注意力重新校准块实现了最先进的性能
B.3D 数据表示
三维数据可以使用四种方法表示。
如图 1 所示:(a) 多视图、(b) 体素网格、(c) 点云 (4) 三角形网格。

- 基于多视图的方法将3D对象表示为来自不同视点的一组图像。多视图方法可以通过将 3D 对象表示为一组 2D 图像来减小维度。但是,它不会显示 3D 特征,并且一个对象需要多个数据集。
- 基于体素的方法是一种将对象转换为体素网格的表达式形式。体素是适合将 2D 处理方法自然扩展到 3D 的数据表示形式。但是,由于体素具有许多稀疏部分,并且以网格单元形式表示,因此无法有效捕获3D对象的细节,并且会产生很高的计算成本。
- 基于点云的方法以3D坐标集表示。点云广泛用于3D对象和场景,如今可以使用3D扫描仪,深度相机和LIDAR设备获得许多3D点云数据集。
- 三角形网格表示为近似几何表面的三角形面的集合,可以看作是从连续几何表面采样的3D点的集合。基于网格的方法旨在以易于渲染的方式表示表面。三角形网格最初是为计算机图形创建的,但对于3D视觉也很有用。
本研究结合了 3D 点云数据,因为点云对象模型比多视图、体素和基于网格的方法更逼真,并且相关的输入数据处理具有较低的计算成本。使用ModelNet40和ShapeNet(3D点云基准数据集)进行了分类和分割实验。
C. Geometric Deep Learning 几何深度学习
III. Method
- 我们提出的模型受到DGCNN模型[12]的显着影响。
- 基于边卷积,捕获点之间的几何特征(或边特征),并学习边缘特征。
- DGCNN模型是基于多层感知器(MLP)构建的,
- 而我们通过添加自己的跳接网络和重新校准块来构建更深,更快的网络。
A. Classification Model
1) Pipeline Model
- 如图2所示,spatial transform block(空间变换块)和edge convolution blocks(边缘卷积块)是骨干模型的主要元素。
- 空间变换块旨在通过应用估计的3 × 3矩阵将点云输入与规范空间对齐。
- 为了估计这个3 × 3矩阵,使用了一个<连接每个点和k个相邻点之间的坐标差的>张量 (图3(a))。
- k个最近邻和点的坐标之间的坐标差是串联的。
- 因此,如图3(a) 所示,k-NN图后的特征图大小为n × k × (3 + 3) = n × k × 6。
- 边缘卷积块计算每个点的边缘特征,并应用池化函数以输出具有n × n形状的张量。
- 这里,n是作为输入进入的点数,
是所应用的MLP的大小 (图3(b))。


- 边卷积块的详细描述如下。
- 假设输入了F维点云数据集X = {p1,p2,·,pn}
。
- 对于大多数3D点云数据,F = 3,pi = (xi,yi,zi)。当添加纹理或颜色等信息时,F会增加。
- 基于此F维点云数据集X,我们配置了一个有向图G = (V,E),其中包括V = {p1,p2,·,pn} 作为顶点集,而E
V × V代表边集。边集表示如下:
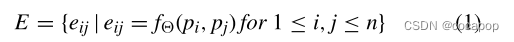
其中:fΘ 是一个非线性函数,具有RF×RF→RF′ 和Θ 是一个可学习的参数。基于此配置V 和E ,G 被构造为k -最近邻图并反映在边缘卷积块中。函数fΘ 定义边要素的表示方式如下:

此非对称函数结合了以pi为中心的全局形状结构和以pj − pi为中心的局部邻域。最后,通过MLP的第l条通道的边缘特征表示如下: