文章目录
- 前言
- 改变 View 的属性,进行旋转、缩放、平移
- 输出 View 的属性
- 使用 matrix 映射 view 变换后的外矩形
- 前(左)乘(preXxx)、后(右)乘(postXxx) 对映射结果的影响
- 前(左)乘(preXxx) 的意义
- 后(右)乘(postXxx)
- 结论
来张图

前言
Android View 通过平移、旋转、缩放后,顶点映射
之前写的这个文章,里面用到的是 matrix.mapPoints() 通过 矩形的4个点来映射出新的4个点。
个人以为这就会得到正确的结果。
最近呢,就想着,验证一下这个是不是正确的
验证想法:
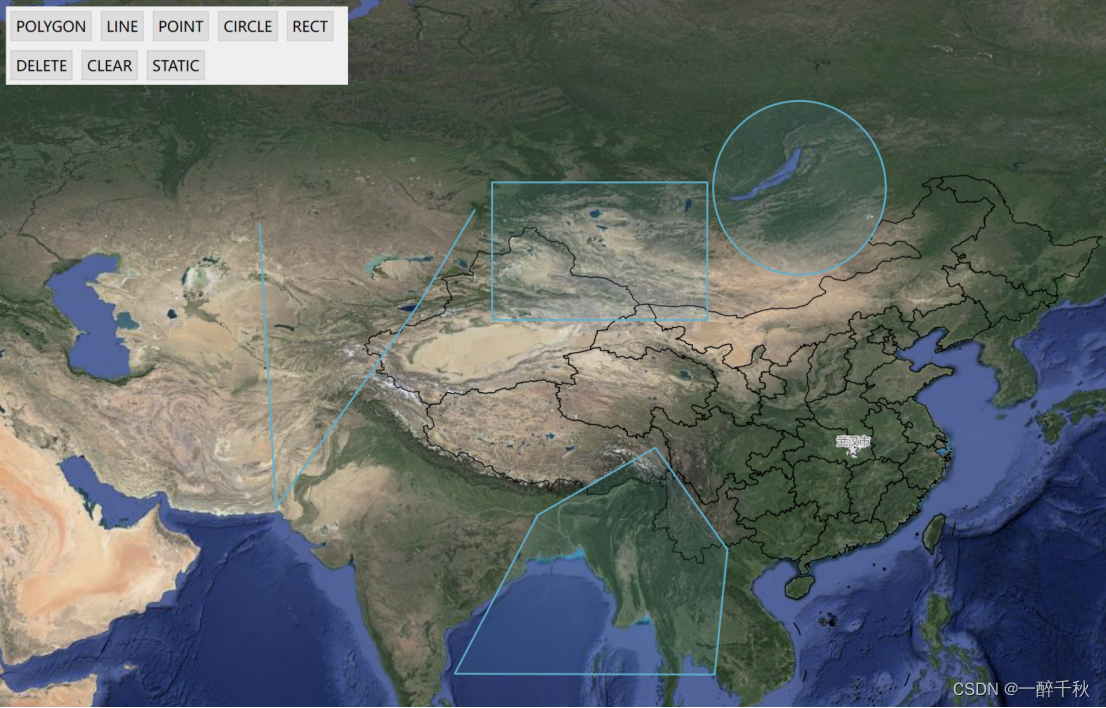
“基于 变换后的 ltrb,加一个自定义 view layout; 有最外层 view那么大; 当 view 变换后,在 layout 上以 ltrb为圆心, 画出一个小圆”
最终发现,旋转 用 matrix#mapPoints() 会有问题;但用 matrix#mapRect() 就正常了
改变 View 的属性,进行旋转、缩放、平移
// View 通过如下操作,在平移、旋转、缩放后,其本身的 left、top、right、bottom、width、height是没有变化的
private fun selfTransform(view: View, tx: Float, ty: Float, rx: Float, ry: Float, sx: Float, sy: Float) {
view.translationX = tx
view.translationY = ty
val px = view.pivotX
val py = view.pivotY
view.pivotX = view.left + view.width/2f
view.pivotY = view.top + view.height/2f
// view.rotationX = rx
// view.rotationY = ry
view.rotation = ry
view.scaleX = sx
view.scaleY = sy
view.pivotX = px
view.pivotY = py
}
rotation 是绕一点,进行二维的旋转
rotationX、rotationY,是绕 x轴 、 y 轴进行旋转
输出 View 的属性
private fun selfProperties(view: View) {
logi("self-ltrb: ${view.left}, ${view.top}, ${view.right}, ${view.bottom}")
logi("tx, ty: ${view.translationX}, ${view.translationY}")
logi("rx, ry: ${view.rotationX}, ${view.rotationY}; rotation: ${view.rotation}")
logi("sx, sy: ${view.scaleX}, ${view.scaleY}")
logi("----------------")
}
通过 selfTransform()传参的不同,并调用 selfProperties()后,发现 view 本身的 left、top、right、bottom、width、height是没有变化的
使用 matrix 映射 view 变换后的外矩形
fun mapRect(model: View, dst: RectF, src: RectF) {
val l = model.left.toFloat()
val t = model.top.toFloat()
val r = model.left + model.width.toFloat()
val b = model.top + model.height.toFloat()
val matrix = Matrix()
val cx = l + (r - l) / 2f
val cy = t + (b - t) / 2f
matrix.postScale(model.scaleX, model.scaleY, cx, cy)
matrix.postRotate(model.rotation, cx, cy) // 以view的中心点旋转
matrix.postTranslate(model.translationX, model.translationY)
matrix.mapRect(dst, src)
}
这里遇到一个问题:
当view 的变换顺序是translation(T)、rotate(R)、scale(S)
matrix 中的顺序 用 RST 或 SRT 都会得到正确的结果;但若用 T在最前,就会得出错误结果
前(左)乘(preXxx)、后(右)乘(postXxx) 对映射结果的影响
前(左)乘(preXxx) 的意义
当前矩阵在前(左),新矩阵在后(右)。
如,若当前矩阵为 M,前乘矩阵 A ⇒ M * A
后(右)乘(postXxx)
当前矩阵在后(右),新矩阵在前(左)。
如,若当前矩阵为 M,后乘矩阵 A ⇒ A * M
一般说,平移使用的矩阵加法, 而旋转、缩放使用的是矩阵乘法。
Android Matrix,应用了 齐次坐标, 转换成 3x3 的矩阵。统一使用 矩阵乘法。虽然运算是乘法,但平移操作和旋转、缩放不能交换顺序,交换后,结果不同。
结论
若,translation(T)、rotate(R)、scale(S)
* postXxx(), 当前矩阵在 后/右;
* post->TRS ==> S(R(T))
* post->TSR ==> R(S(T))
*
* post->RST ==> T(S(R))
* post->SRT ==> T(R(S))
* preXxx(),当前矩阵在 左/前;
* pre->TRS ==> T(R(S))
* pre->TSR ==> T(S(R))
*
* pre->RST ==> R(S(T))
* pre->SRT ==> S(R(T))
虽然统一采用了乘法,但 S、R是可交换的。它们和 T 是不可交换的。
从结论看, preXxx 可以完全符合 view变换的顺序。
(说个故事,多年以来,都喜欢用 post,这次突破了自我%^--^%)
Demo完整代码