【WSN定位】加权质心定位算法-Matlab代码

news2025/1/16 15:54:43

文章目录

- 1. 质心定位算法
- 2. 加权质心定位算法
- 3. 部分代码展示
- 4. 效果图展示
- 5. 资源获取说明

摘要：质心定位算法(Centroid Algorithm)是 Nirupama Bulusu等提出的一种无需测距的粗精度定位算法。质心算法的基本思路：利用未知节点通信范围内的所有锚节点进行定位，将所有的锚节点根据其坐标连接起来形成多边形，多边形的几何中心即为未知节点的估计位置。

1. 质心定位算法

图1 质心定位算法原理图

图1 质心定位算法的原理图

如图所示，假设某未知节点 $O (x, y)$ 的通信范围内的锚节点坐标分别为 $H_{1}(x_{1},y_{1})$ 、 $H_{2}(x_{2},y_{2})$ 、 $H_{3}(x_{3},y_{3})$ 、 $H_{4}(x_{4},y_{4})$ 、 $H_{5}(x_{5},y_{5})$ ，通过公式(1)求解，可以得到未知节点的坐标：
$(x,y)=(\frac{x_{1}+x_{2}+...+x_{n}}{n}, \frac{y_{1}+y_{2}+...+y_{n}}{n})\tag{1}$
注：锚节点是否在未知节点 $O (x, y)$ 通信范围内的判定标准为：如果锚节点 $H_{n}(x_{n},y_{n})$ 到未知节点 $O (x, y)$ 的距离小于 $O (x, y)$ 的通信半径，那么锚节点 $H_{n}(x_{n},y_{n})$ 就在未知节点 $O (x, y)$ 的通信范围内。

2. 加权质心定位算法

传统的质心算法在求解过程中只是将未知节点通信范围内所有锚节点的横、纵坐标对应相加取平均，并没有体现出不同位置的锚节点对未知节点的影响不同。因此，提出了加权质心定位算法，该方法综合考虑锚节点与未知节点的远近程度对未知节点的影响，给每个锚节点赋予不同的权值 $w$ ，以此来提高未知节点的坐标精确度。具体实现如下：

首先根据公式(2)计算出 $H_{1}$ 、 $H_{2}$ 到 $H_{n}$ 共 $n$ 个锚节点各自的权重： $w_{1}$ ， $w_{2}$ ， $...$ ， $w_{n}$
$w_{n} =\frac{1}{d_{n} } \tag{2}$
然后结合公式(1)赋予每个锚节点相应的权重，得到公式(3)：
$(x,y)=(\frac{x_{1}w_{1}+x_{2}w_{2}+...+x_{n}w_{n}}{\sum_{i=1}^{n}w_{i}}, \frac{y_{1}w_{1}+y_{2}w_{2}+...+y_{n}w_{n}}{\sum_{i=1}^{n}w_{i}})\tag{3}$

改进后的公式，对于离未知节点更近的锚节点，其被赋予的权重更高，在公式(3)中所占的比重更高，在对未知节点坐标估算中的贡献也就越大。

3. 部分代码展示

% 画出每个待定位节点与所属于的质心的距离，以绿线表示
h5=plot([cent(1,j) Sx(j)],[cent(2,j) Sy(j)],'b');
hold on
%画出每个待定位节点与所属于的加权质心的距离，以红线表示
h6=plot([centx(1,j) Sx(j)],[centx(2,j) Sy(j)],'r');
hold on
title('质心与加权质心定位结果对比')
legend([h1,h2,h3,h4],'锚节点','待定位节点','质心定位','加权质心定位')

% 求出每个待定位节点的定位误差
% SS是待定位节点的真实坐标，MM是质心定位结果坐标，NN是加权质心定位结果坐标
MM=[cent(1,j);cent(2,j)];
e(j)=norm((MM-SS),2)/dm;
NN=[centx(1,j);centx(2,j)];
err(j)=norm((NN-SS),2)/dm;
end

figure(2)
axis([0 n 0 10])
% 绿线表示质心与实际位置的误差
plot(e,'-g.')
hold on
% 红线表示加权质心与实际位置的误差
plot(err,'-r.')
hold on
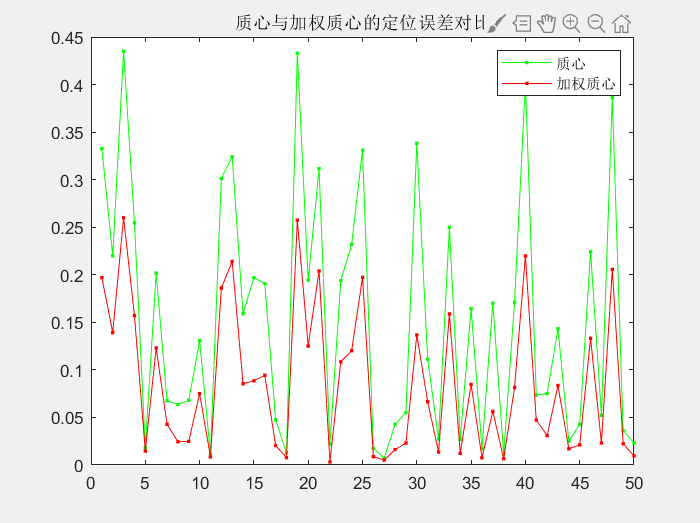
title('质心与加权质心的定位误差对比')
legend('质心','加权质心')

E=sum(e)/n;
ERR=sum(err)/n;
display(['质心定位算法的平均误差为: ', num2str(E)]);
display(['加权质心定位算法的平均误差为: ', num2str(ERR)]);