4种吃子跳棋

news2025/1/19 20:34:01

目录

一，双玩家吃子跳棋

玻璃跳棋

大人物跳棋

二，单玩家吃子跳棋

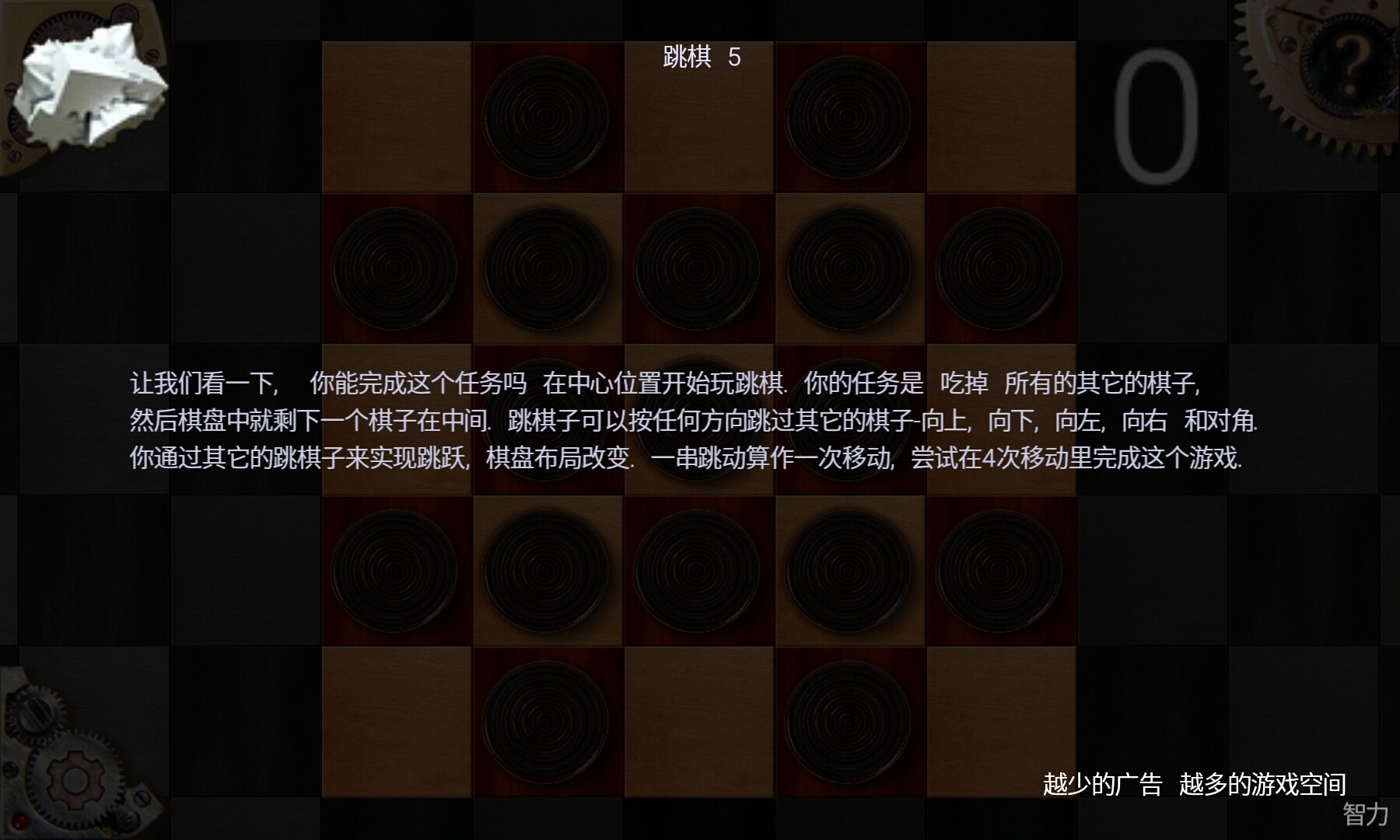
智力游戏67跳棋（5）

一个挑战

跳瓶盖

欢乐跳跳棋

三，单玩家多目吃子跳棋——Hopping dots

1，Hopping dots

2，规则

3，问题的简化

（3.1）局面的数量

（3.2）编号

（3.3）记录所有的边（不考虑方向）

（3.4）深度优先搜索的可能性分析

4，原问题的求解

一，双玩家吃子跳棋

玻璃跳棋

在线play

规则：棋子只能斜着往前移动一步，或者连续吃子若干次。

吃子不限制方向，且可以连续进行。

棋子到达对方底线可以变成皇后，皇后可以无视1格距离的限制。

要想消灭一个皇后还不太容易，首先要尽可能多的把棋子变成皇后，然后设局卡住对方皇后，使其不能在边缘苟着。

示例：

到了这一步，3个皇后就把对方的皇后完全堵死了。

大人物跳棋

在线paly

规则：

（1）人物可以跳到自己的相邻的棋子上，有人物的棋子到达对方底线则获胜，或者把对方棋子吃完获胜。

（2）普通棋子只能斜着往前移动一步或者连续吃子若干次。有人物的棋子可以斜着往前移动或吃子，也可以斜着往后移动或吃子。

（3）普通棋子到达对方底线则变成双子，可以斜着往前，也可以斜着往后。

到了这一步，后面很快就赢了。 

二，单玩家吃子跳棋

单玩家吃子跳棋就是要把所有棋子吃掉，只剩下最后一个棋子。

独立钻石棋就是典型的单玩家吃子跳棋，而且独立钻石棋是初始只有1个缺口。

智力游戏67跳棋（5）

不得不说，这个游戏很难，而且编程也很难。

花了不少功夫，才得到一个勉强给出解的程序。

最难的地方就是，如何避免死循环，也就是（2,0）和（3,1）之间一直跳转的死循环

代码：

#include<iostream>
using namespace std;

int number = 4;

bool move(int list[][5], int i, int j)		//判断是否能够从（i,j）开始跳，最多只用number步
{
	if (list[i][j] == 0)return false;
	int save[5][5], save_number = number;
	for (int i = 0; i < 5; i++)			//保存list，用于回溯的时候还原list
		for (int j = 0; j < 5; j++)save[i][j] = list[i][j];
	if (number <= 0)
	{
		int sum = 0;	//判断是不是已经成功了
		for (int i = 0; i < 5; i++)for (int j = 0; j < 5; j++)sum += list[i][j];
		if (sum == 1 && list[2][2] == 1)return true;
		return false;
	}
	if (i>1 && list[i - 1][j] == 1 && list[i - 2][j] == 0)	//满足往上跳的条件
	{
		list[i][j]--;
		list[i - 1][j]--;
		list[i - 2][j]++;
		if (move(list, i - 2, j))
		{
			cout << i << " 上 " << j << endl;
			return true;
		}
	}
	else if (i<3 && list[i + 1][j] == 1 && list[i + 2][j] == 0)	//满足往下跳的条件
	{
		list[i][j]--;
		list[i + 1][j]--;
		list[i + 2][j]++;
		if (move(list, i + 2, j))
		{
			cout << i << " 下 " << j << endl;
			return true;
		}
	}
	else if (j>1 && list[i][j - 1] == 1 && list[i][j - 2] == 0)	//满足往左跳的条件
	{
		list[i][j]--;
		list[i][j - 1]--;
		list[i][j - 2]++;
		if (move(list, i, j - 2))
		{
			cout << i << " 左 " << j << endl;
			return true;
		}
	}
	else if (j<3 && list[i][j + 1] == 1 && list[i][j + 2] == 0)	//满足往右跳的条件
	{
		list[i][j]--;
		list[i][j + 1]--;
		list[i][j + 2]++;
		if (move(list, i, j + 2))
		{
			cout << i << " 右 " << j << endl;
			return true;
		}
	}
	else if (i>1 && j>1 && list[i - 1][j - 1] == 1 && list[i - 2][j - 2] == 0)	//满足往左上跳的条件
	{
		list[i][j]--;
		list[i - 1][j - 1]--;
		list[i - 2][j - 2]++;
		if (move(list, i - 2, j - 2))
		{
			cout << i << " 左上 " << j << endl;
			return true;
		}
	}
	else if (i<3 && j>1 && list[i + 1][j - 1] == 1 && list[i + 2][j - 2] == 0)	//满足往左下跳的条件
	{
		list[i][j]--;
		list[i + 1][j - 1]--;
		list[i + 2][j - 2]++;
		if (move(list, i + 2, j - 2))
		{
			cout << i << " 左下 " << j << endl;
			return true;
		}
	}
	else if (i>1 && j<3 && list[i - 1][j + 1] == 1 && list[i - 2][j + 2] == 0)	//满足往右上跳的条件
	{
		list[i][j]--;
		list[i - 1][j + 1]--;
		list[i - 2][j + 2]++;
		if (move(list, i - 2, j + 2))
		{
			cout << i << " 右上 " << j << endl;
			return true;
		}
	}
	else if (i<3 && j<3 && list[i + 1][j + 1] == 1 && list[i + 2][j + 2] == 0)	//满足往右下跳的条件
	{
		list[i][j]--;
		list[i + 1][j + 1]--;
		list[i + 2][j + 2]++;
		if (move(list, i + 2, j + 2))
		{
			cout << i << " 右下 " << j << endl;
			return true;
		}
	}

	number--;
	for (int ii = 0; ii < 5; ii++)		//还有8个方向都跳不了的情况，以及可以跳但是我选择不跳的情况
	for (int jj = 0; jj < 5; jj++)
	{
		if (ii == i&&jj == j)continue;
		if (move(list, ii, jj))return true;
	}

	for (int i = 0; i < 5; i++)for (int j = 0; j < 5; j++)list[i][j] = save[i][j];//还原list	
	number = save_number;
	return false;
}

int main()
{
	int list[5][5];				//list用来表示状态，0表示空格，1表示有棋子
	for (int i = 0; i < 5; i++)	for (int j = 0; j < 5; j++)
	{
		if (i == 1 || i == 3 || j == 1 || j == 3)list[i][j] = 1;
		else list[i][j] = 0;
	}
	list[2][2] = 1;
	move(list, 2, 2);
	cout << endl << "注意，输出的顺序是反着的";
	system("pause>nul");
	return 0;
}

输出：

4 右上 2
2 右下 0
2 左 2
0 左下 4
2 上 4
4 上 4
4 右 2
4 右 0
2 下 0
0 左下 3
1 右 0
3 左上 2
0 左 2
2 上 2
注意，输出的顺序是反着的

一个挑战

Taptap游戏，只有一关。

任选一个格子去掉棋子，变成空格，然后按照独立钻石棋的规则消除棋子，最后只剩一颗棋子。

先选中第四行第一个格子消掉，然后再把上面的消掉：

 

 

跳瓶盖

在线play

（7）

  

（11）

  

（13）

  

欢乐跳跳棋

在线play

（1）

 

 （2）

 

上面的《一个挑战》其实就可以选择去掉最上面的棋子变成本关卡，不过因为那个是我先玩的，我想到的是去掉第四行第一列的另一种解法。

本关卡首先可以变成：

这后面就和《一个挑战》一样了。

（3）

 

 

 

 

三，单玩家多目吃子跳棋——Hopping dots

 这一章，我想完整的讨论一个游戏，叫Hopping dots，被翻译为逻辑难题。

关键词：独立钻石棋、深度优先搜索、可能性分析、状态压缩、动态规划的备忘录方法

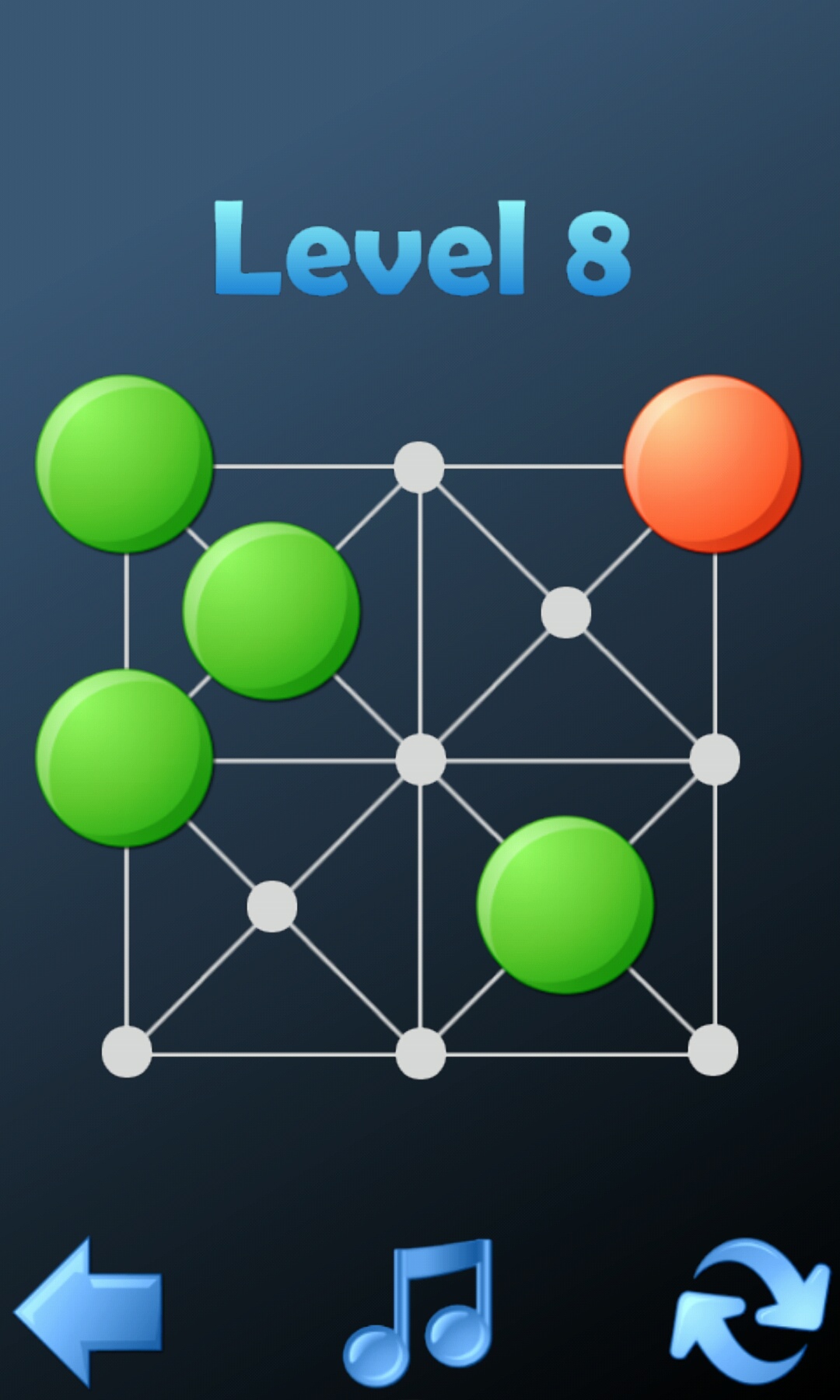
1，Hopping dots

 APK下载链接（Hopping dots 1.1）：资源分享汇总_nameofcsdn的博客-CSDN博客

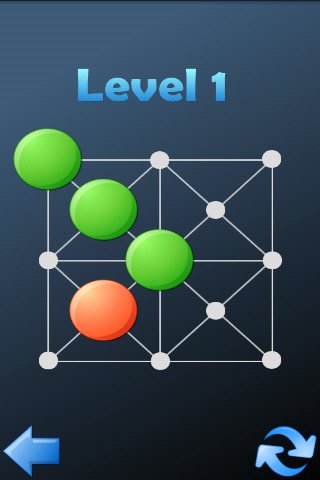
游戏界面（下图为第一关）

棋盘：由13个点组成

棋子：1个红子和若干个绿子

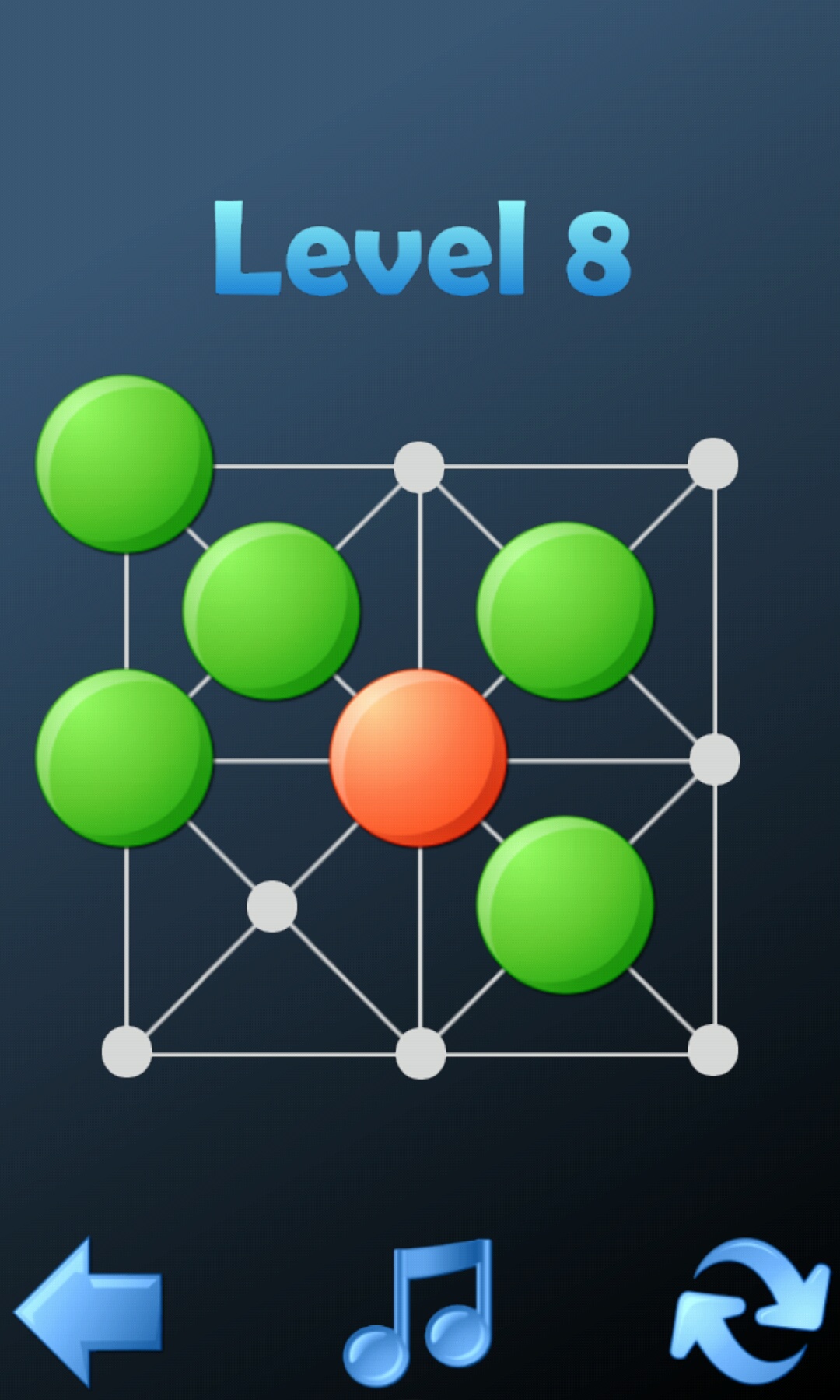
2，规则

按照独立钻石棋的规则进行吃子，最后只剩下一个子，且为红子，即为胜利。（无论红子在何处）

这是我自己总结的规则，非常简洁，初一看貌似不准确，仔细一想实际上和官方的定义是一样的。

棋子最多有12个，最少有1个。

13个棋子肯定是死局面（无法胜利的局面），因为没法进行操作。

12个棋子的局面中，存不存在活局面（能够胜利的局面），这个暂且不知。

每次操作，棋子数量都是少1，所以，任何局面，最多只能再进行11次操作。

3，问题的简化

问题的简化版：只有绿子没有红子，只要最后只剩下一个子即为胜利（同样不论位置）

这样的版本就更接近独立钻石棋了，对于玩家来说，原问题和问题的简化版差异并不是很大，玩起来难度差不多。而对于想做理论分析的笔者来说，原问题分析起来很繁琐，掩盖了很多规律。

如果只是想直接尝试编写深度优先搜索的程序解决问题，其实是不需要简化的，但是如果要严谨一些，先从理论上分析可能性大小，所以如此简化正是第一步要做的事情。

（3.1）局面的数量

有13个点是可能有子的，所以局面的数量为2^13=8192

其中还包括了大量的死局面，具体有多少活局面，我们并不关心。

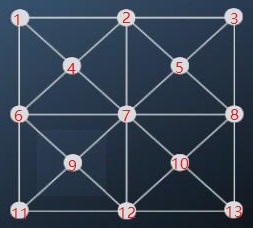
（3.2）编号

（3.3）记录所有的边（不考虑方向）

不难数出，一共有16条边

以2、6、8、12为中点的边各有1条，如1-2-3

以4、5、9、10为中点的边各有2条，如1-4-7，2-4-6

以7为中点的边有4条，如2-7-12，4-7-10

之所以不考虑方向，是因为任何时刻，一条边最多对应一种可行操作，

以边1-2-3为例，同一局面下，“从1跳到3”和“从3跳到1”不可能都是可行的操作。

注意到，每条边的3个数都是等差数列，所以一条边只需要2个数字记录下来起点和终点，

这样，便可以用2个长度为16的数组来记录下16条边了。

int st[16] = { 1, 1, 3, 11, 1, 2, 2, 3, 6, 7, 8, 7, 4, 5, 6, 2 };
int en[16] = { 3, 11, 13, 13, 7, 6, 8, 7, 12, 11, 12, 13, 10, 9, 8, 12 };

（3.4）深度优先搜索的可能性分析

因为最多只能进行11次操作，所以深度优先搜索的深度不深。现在需要计算的是，每一次操作有多少种选择？

（3.4.1）任一局面有多少种选择

我们需要一个函数，输入一个局面，输出一个数值，告诉我们有多少种选择。

如何输入呢？使用状态压缩最为方便。

13个点，每个点对应一位，1表示有子，0表示没有子，这样，8192个局面便可以和8192个13位二进制数一一对应了。

输入之后，函数就可以直接计算出有多少种选择了，时间为O（1）

有了这个函数，只要从0到8191枚举n，就能求出f（n）的最大值了，结果是10

代码：

#include <iostream>
using namespace std;

int st[16] = { 1, 1, 3, 11, 1, 2, 2, 3, 6, 7, 8, 7, 4, 5, 6, 2 };
int en[16] = { 3, 11, 13, 13, 7, 6, 8, 7, 12, 11, 12, 13, 10, 9, 8, 12 };

int f(int n)
{
	int r = 0, s, e, m;
	for (int i = 0; i < 16; i++)
	{
		s = st[i], e = en[i], m = (s + e) / 2;
		if ((n >> (13 - m)) & 1)r += ((n >> (13 - s)) & 1) ^ ((n >> (13 - e)) & 1);
	}
	return r;
}

int main()
{
	int maxx = 0;
	for (int n = 0; n < 8192; n++)if (maxx < f(n))maxx = f(n);
	cout << maxx;
	return 0;
}

（3.4.2）深度优先搜索的复杂度

前面分别算出，一个局面最多能再进行11次操作，每次操作最多10种选择，那么，用深度优先搜索解决这个问题最多需要10^11次枚举计算。这是一个很大的数，普通的笔记本要算很久。

然而，我们不难发现，并非每次操作都有10种选择，比如只剩2个子的时候最多只有2种选择。

那么如果一个局面有k（1<k<13）个子，这个局面最多有多少种选择？

只需利用上面的函数f即可。

代码：

#include <iostream>
using namespace std;

int st[16] = { 1, 1, 3, 11, 1, 2, 2, 3, 6, 7, 8, 7, 4, 5, 6, 2 };
int en[16] = { 3, 11, 13, 13, 7, 6, 8, 7, 12, 11, 12, 13, 10, 9, 8, 12 };
int num[14];//k个棋子的所有局面中最多有多少种选择

void f(int n)
{
	int r = 0, s, e, m, k = 0;
	for (int i = 0; i < 16; i++)
	{
		s = st[i], e = en[i], m = (s + e) / 2;
		if ((n >> (13 - m)) & 1)r += ((n >> (13 - s)) & 1) ^ ((n >> (13 - e)) & 1);
	}
	while (n)
	{
		k += n & 1;
		n /= 2;
	}
	if (num[k] < r)num[k] = r;
}

int main()
{
	for (int i = 0; i < 14; i++)num[i] = 0;
	for (int n = 0; n < 8192; n++) f(n);
	for (int i = 2; i <= 12; i++)cout << num[i] << "  ";
	return 0;
}

运行结果：

2  4  7  7  9  10  9  9  8  6  4

2*4*7*7*9*10*9*9*8*6*4=548674560，所以任何一个局面，进行深度优先搜索的话，最多需要约5亿次枚举计算

计算机一秒可以进行约1亿次计算，所以这个时间是可以接受的。

4，原问题的求解

原问题由于有红子的限制，所以编程起来要复杂一些，但是需要枚举的情况少一些。

这样，就可以深度优先搜索求解了，同时，因为局面的数量很有限，所以用动态规划的备忘录方法来避免重复工作。

代码：

#include <iostream>
#include<stack>
using namespace std;

int r[8192][14];//0表示未知，-1表示死局面，1表示活局面
int st[16] = { 1, 1, 3, 11, 1, 2, 2, 3, 6, 7, 8, 7, 4, 5, 6, 2 };
int en[16] = { 3, 11, 13, 13, 7, 6, 8, 7, 12, 11, 12, 13, 10, 9, 8, 12 };
stack<int>ans;

bool f(int n, int k)
{
	if (n == (n&-n))return true;//只有1个子
	if (r[n][k] < 0)return false;
	int s, e, m;
	for (int i = 0; i < 16; i++)
	{
		s = st[i], e = en[i], m = (s + e) / 2;
		if (m == k)continue;//红子不能被跳过
		if (!((n >> (13 - m)) & 1))continue;
		if (!(((n >> (13 - s)) & 1) ^ ((n >> (13 - e)) & 1)))continue;
		int nn, kk = k, tem;
		if (k == s || k == e)kk = s + e - k;
		tem = (1 << (13 - s)) + (1 << (13 - e));
		nn = n - (n&tem) + tem - (n&tem) - (1 << (13 - m));
		if (f(nn, kk))
		{
			ans.push(i);
			m = -1;
			break;
		}
	}
	if (m == -1)return true;
	r[n][k] = -1;
	return false;
}

int main()
{
	int n = 0, k;//n表示无颜色局面，k表示红子位置
	cout << "按照编号\n1    2    3\n  4    5\n6    7    8\n  9    10\n11   12   13\n";
	cout << "即从上到下，从左往右，依次输入每个格子\n1表示有子，0表示没有子，全部用空格隔开\n";
	for (int i = 1; i <= 13; i++)
	{
		cin >> k;
		n = n * 2 + k;
	}
	cout << "输入红子所在格子的序号（1-13）\n";
	cin >> k;
	for (int i = 0; i < 8192; i++)for (int j = 0; j < 14; j++)r[i][j] = 0;
	while (!ans.empty())ans.pop();
	f(n, k);
	cout << "答案为：（一行表示一次操作，每行2个整数分别代表起点和终点的序号）\n";
	while (!ans.empty())
	{
		int i = ans.top();
		ans.pop();
		cout << st[i] << "   " << en[i] << endl;
	}
	return 0;
}

示例：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/434839.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

说过的话就一定要办到 - redo日志

说过的话就一定要办到 - redo日志

一、什么是redo日志&#xff1f; 如果我们只在内存的 Buffer Pool 中修改了页面&#xff0c;假设在事务提交后突然发生了某个故障&#xff0c;导致内存中的数据都失效了&#xff0c;那么这个已经提交了的事务对数据库中所做的更改也就跟着丢失了&#xff0c;这会导致事务会失去…
阅读更多...
火力全开，重新定义蓝牙耳机！新一代南卡OE Pro不入耳式蓝牙耳机震撼来袭

火力全开，重新定义蓝牙耳机！新一代南卡OE Pro不入耳式蓝牙耳机震撼来袭

中国专业声学品牌Nank南卡&#xff0c;在近期推出了南卡OE Pro不入耳蓝牙耳机&#xff0c;是业内首款功能配置齐全的蓝牙耳机&#xff0c;以创新开放式听音方式&#xff0c;让更多人感受到不入耳开放式耳机带来的魅力之处。据了解&#xff0c;有不少媒体猜测&#xff0c;南卡OE…
阅读更多...
工作面试老大难 - 锁

工作面试老大难 - 锁

一、概述 为保证数据的一致性和完整性&#xff0c;需要对 事务间并发操作进行控制 &#xff0c;因此产生了 锁 。锁冲突 也是影响数据库 并发访问性能 的一个重要因素。所以锁对数据库而言显得尤其重要&#xff0c;也更加复杂。 二、并发问题 MySQL并发事务访问相同记录 &am…
阅读更多...
硬件设计--DAPLINK设计

硬件设计--DAPLINK设计

1 参考网站 1、打造属于你自己的STM32下载器调试器--------DAPLink 2、ARMmebed官方开源代码DAPLink 3、ARMmebed官方开源代码DAPLink github加速网站 4、ARMmebed官方开源硬件旧版 5、ARMmebed官方开源硬件新版 6、自制DAPLink – ARM官方源码以及STM32F103C8T6 7、如何做一个…
阅读更多...
软件测试之测试名词解释

软件测试之测试名词解释

1. 白盒测试&#xff0c;英文是white-box testing 是通过程序的源代码进行测试而不使用用户界面。这种类型的测试需要从代码句法发现内部代码在算法&#xff0c;溢出&#xff0c;路径&#xff0c;条件等等中的缺点或者错误&#xff0c;进而加以修正。 2. 黑盒测试&#xff0c;英…
阅读更多...
word脚标【格式：第X页（共X页）】

word脚标【格式：第X页（共X页）】

不得不吐槽一下这个论文&#xff0c;真的我好头疼啊。我又菜又不想改。但是还是得爬起来改 &#xff08;是谁大半夜不能睡觉加班加点改格式啊&#xff09; 如何插入页码。 格式、要求如下: 操作步骤&#xff1a; ①双击页脚&#xff0c;填好格式&#xff0c;宋体小四和居中都…
阅读更多...
除了 Swagger，这个开源 API 管理工具生成文档更高效

除了 Swagger，这个开源 API 管理工具生成文档更高效

提起 Swagger&#xff0c;经常接触接口开发的朋友&#xff0c;一定知道并且都熟练使用了。 Swagger 是一个用于生成、描述和调用 RESTful 接口的 Web 服务。通俗的来讲&#xff0c;Swagger 就是将项目中所有&#xff08;想要暴露的&#xff09;接口展现在页面上&#xff0c;并且…
阅读更多...
VMware ESXi 8.0U1 发布 - 领先的裸机 Hypervisor

VMware ESXi 8.0U1 发布 - 领先的裸机 Hypervisor

请访问原文链接&#xff1a;https://sysin.org/blog/vmware-esxi-8-u1/&#xff0c;查看最新版。原创作品&#xff0c;转载请保留出处。 作者主页&#xff1a;sysin.org 2023-04-18, VMware vSphere 8.0U1 发布。 详见&#xff1a;VMware vSphere 8 Update 1 新增功能 产品简…
阅读更多...
ai智能写作助手-ai自动写作软件

ai智能写作助手-ai自动写作软件

为什么要用ai智能写作工具 在数字化时代&#xff0c;AI&#xff08;人工智能&#xff09;技术已经被广泛应用于各种领域&#xff0c;其中之一是写作。AI智能写作工具是利用自然语言处理技术和机器学习算法来生成高质量的文章、博客、新闻稿等。这些工具不仅提供了便捷、高效的…
阅读更多...
校园网策列及思路

校园网策列及思路

解决思路一&#xff1a; 适合以下情况也是我现在的学校校园网大概情况&#xff1a; 内网不认证情况下可以互联&#xff0c;除了几个常见端口封闭&#xff08;目前已知3389&#xff09;&#xff0c;要联网必须认证登录&#xff0c;而且一个号最多两台设备&#xff08;甚至有时候…
阅读更多...
FANUC机器人DCS功能基本介绍

FANUC机器人DCS功能基本介绍

FANUC机器人DCS功能基本介绍 1. 定义 DCS（Dual Check Safety）位置/速度检查功能；利用机器人控制柜中两个独立CPU进行电机速度和位置数据的检查，实时检查位置和速度误差，并通过两个独立的通道关闭电机电源。 DCS功能可以有效地节约占地面积。 DCS功能可以防止机器人工具…
阅读更多...
工业通讯应用中主流的常用协议Modbus协议

工业通讯应用中主流的常用协议Modbus协议

智联物联技术分享&#xff0c;本期为大家介绍工业通讯常用的主流协议Modbus协议。 Modbus协议的前身叫做Mod协议&#xff0c;常被用于Modicon公司的PLC控制器中&#xff0c;后来Modicon被Schneider收购后随之改名为我们如今所熟悉的modbus协议&#xff0c;现如今广泛应用在物联…
阅读更多...
【高级数据结构】红黑树

【高级数据结构】红黑树

本文整理红黑树学习过程中的知识点和底层代码实现。 目录 基本概念1、介绍2、应用3、性质 实现红黑树1、原理2、操作1&#xff09;查找2&#xff09;插入3&#xff09;删除 和其他相似结构的对比1、二叉搜索树&#xff08;BST&#xff09;2、AVL树1&#xff09;例子2&#xff0…
阅读更多...
Dubbo+Zookeeper 实现服务远程调用

Dubbo+Zookeeper 实现服务远程调用

文章目录 一、Dubbo 架构图二、Zookeeper 注册中心三、SpringBoot 整合 Dubbo3.1 添加依赖3.2 配置服务端3.3 配置消费端3.4 启动测试 四、Dubbo-admin 管理中心4.1 部署服务端4.2 部署前端4.3 访问控制台 提示&#xff1a;以下是本篇文章正文内容&#xff0c;Java 系列学习将会…
阅读更多...
Visual Assist X安装失败解决办法

Visual Assist X安装失败解决办法

最近重装了VS2017&#xff0c;在重装之前卸载了VA助手&#xff0c;但是等到装好VS再去装VA助手时&#xff0c;总是提示以下错误信息&#xff1a; Visual Assist Installer : An error was reported by Visual Studio VSIXInstaller. See the next window for access to its err…
阅读更多...
ElasticJob

ElasticJob

官网 :: ElasticJob ElasticJob 是面向互联网生态和海量任务的分布式调度解决方案&#xff0c;由两个相互独立的子项目 ElasticJob-Lite 和 ElasticJob-Cloud 组成。 它通过弹性调度、资源管控、以及作业治理的功能&#xff0c;打造一个适用于互联网场景的分布式调度解决方案&…
阅读更多...
如何给厂区做导航地图？智能工厂导航地图解决方案公司

如何给厂区做导航地图？智能工厂导航地图解决方案公司

如何给厂区做导航地图&#xff1f;在智慧园区中&#xff0c;基于园区的电子地图地图使用的重要性越来越凸显。但目前在园区信息化应用形式中&#xff0c;广泛缺乏专业电子地图的使用&#xff0c;主要原因是&#xff1a;一是地图系统(GIS)实现繁复&#xff0c;与其他展会业务系统…
阅读更多...
GateWay微服务网关的搭建

GateWay微服务网关的搭建

服务网关 没有服务网关 问题&#xff1a;地址太多|安全性|管理问题 访问商品服务 http://ip地址:9001/goods/findAll 访问广告服务 http://ip地址:9002/brand/findAll 访问用户服务 http://ip地址:9003/user/findAll 在有网关的情况下&#xff0c;我们配置网关端口号为…
阅读更多...
Vue2之webpack篇（二）Loader

Vue2之webpack篇（二）Loader

目录 一、loader处理css 1、css文件的创建 2、安装css-loader 3、配置 4、打包 5、最终效果 二、loader处理图片 1、引入图片 2、安装file-loader 3、配置module 4、webpack打包 三、ES6转ES5 1、介绍 2、安装babel-loader 3、webpack.config.js配置 4、webpack打…
阅读更多...
C++数据结构：二叉树

C++数据结构：二叉树

二叉树 每个结点最多只有二棵子树&#xff0c;也就是二叉树中没有度大于2的结点。二叉树的子树有左右之分&#xff0c;严格区分左孩子、右孩子&#xff0c;其次序不能颠倒 二叉树五种基本形态 特殊二叉树 斜树 所有节点都只有左子树的二叉树叫做左斜树&#xff0c;所有节点都…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023