二叉树

每个结点最多只有二棵子树，也就是二叉树中没有度大于2的结点。二叉树的子树有左右之分，严格区分左孩子、右孩子，其次序不能颠倒

二叉树五种基本形态

特殊二叉树

斜树

所有节点都只有左子树的二叉树叫做左斜树，所有节点都只有右子树的二叉树叫做右斜树。左斜树和右子树统称为斜树。

斜树已经退化成线性结构，二叉树在查找上表现出来优异性能在斜树得不到体现。

满二叉树

所有的节点都同时具有左子树和右子树。所有的叶子节点都在同一层上。

完全二叉树

完全二叉树从根结点到倒数第二层满足满二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。

二叉树性质

在二叉树的第i层上至多有2i-1(i ≥1)。
深度为k的二叉树至多有个结点(k≥1)。
具有n个结点的完全二叉树的深度为。
在任意一棵二叉树中，若终端结点的个数为，度为2的结点数为，则。
对于有n个结点的完全二叉树中编号为i的结点:
- 若,则结点i是二叉树的根
- 若,则其双亲节点为
- 若,则结点i的左子节点为2i
- 若,则结点i无左子结点
- 若,则结点i的右子结点为
- 若,则结点i无右子结点

二叉树的典型遍历方式

前序遍历

如果二叉树为空，则无操作，直接返回。
如果二叉树非空，则执行以下操作：
A. 访问根结点；
B. 先序遍历左子树
C. 先序遍历右子树。

中序遍历

如果二叉树为空，则无操作，直接返回。
如果二叉树非空，则执行以下操作：
A. 中序遍历左子树；
B. 访问根结点；
C. 中序遍历右子树。

后序遍历

如果二叉树为空，则无操作，直接返回。
如果二叉树非空，则执行以下操作：
A. 后序遍历左子树；
B. 后序遍历右子树；
C. 访问根结点。

二叉树的存储

顺序存储结构

用一维数组存储二叉树中的结点，必须把二叉树的所有结点安排成一个恰当的序列，结点在这个序列中的相互位置能反映出结点之间的逻辑关系。用编号的方法从树根起，自上层至下层，每层自左至右地给所有结点编号。这样既能够最大可能地节省存储空间，又可以利用数组元素的下标值确定结点在二叉树中的位置，以及结点之间的关系。

满二叉树

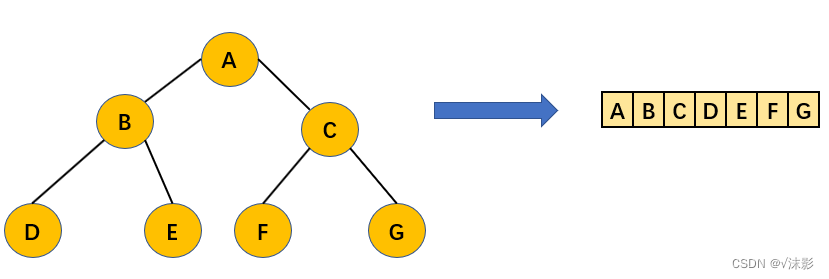
对于一般的非完全二叉树来说，如果仍然按照从上到下、从左到右的次序存储在一维数组中，则数组下标之间不能准确反映树中结点间的逻辑关系，可以在非完全二叉树中添加一些并不存在的空结点使之变成完全二叉树

优点：读取某个指定的节点的时候效率比较高
缺点：有可能对存储空间造成极大的浪费，在最坏的情况下，一棵深度为k的右斜树，它只有k个结点，却需要个结点存储空间。这显然是对存储空间的严重浪费，所以顺序存储结构一般只用于完全二叉树或满二叉树。

链式存储结构

用链表来表示一棵二叉树，每个结点最多有两个孩子，因此，每个结点除了存储自身的数据外，还应设置两个指针分别指向左、右孩子结点。当没有孩子结点时，相应的指针域置为空。

优点：相对二叉树比较大的时候浪费空间较少
缺点：有可读取某个指定节点的时候效率偏低。

Demo

MyTree.h

#pragma once
#include <vector>
#include <iostream>
#include <queue>
using namespace std;
/********************************************
*******************顺序存储*******************
*********************************************/
template<typename T>
class CMyTree_Arr
{
	vector<T> vec_buff;
public:
	CMyTree_Arr();
	~CMyTree_Arr();
	void clera();
	void initTree(T arr[], size_t length);
	bool find(T const& findVal)const;
	void appendNode(T const& data);
	void prePrint(int index = 1);
	void inPrint(int index = 1);
	void posPrint(int index = 1);
private:
	int _find(T const& finaVal)const;
};

template <typename T>
CMyTree_Arr<T>::CMyTree_Arr()
{
	vec_buff.clear();
}

template <typename T>
CMyTree_Arr<T>::~CMyTree_Arr()
{
	vec_buff.clear();
}

template <typename T>
void CMyTree_Arr<T>::clera()
{
	vec_buff.clear();
}

template <typename T>
void CMyTree_Arr<T>::initTree(T arr[], size_t length)
{
	vec_buff.clear();
	vec_buff.push_back(-1);
	vec_buff.insert(vec_buff.end(), arr, arr + length);
	//vector<T> temp_vector(arr, arr + length);
	//vec_buff = temp_vector;
}

template <typename T>
bool CMyTree_Arr<T>::find(T const& findVal) const
{
	return _find(findVal) != -1;
}

template <typename T>
void CMyTree_Arr<T>::appendNode(T const& data)
{
	vec_buff.push_back(data);
}

template <typename T>
void CMyTree_Arr<T>::prePrint(int index)
{
	if (index < vec_buff.size() && index >= 0)
	{
		cout << vec_buff[index] << " ";//根
		prePrint(2 * index);//前序遍历左子树
		prePrint(2 * index + 1);//前序遍历右子树
	}
}

template <typename T>
void CMyTree_Arr<T>::inPrint(int index)
{
	if (index < vec_buff.size() && index >= 0)
	{
		inPrint(2 * index);//中序遍历左子树
		cout << vec_buff[index] << " ";//根
		inPrint(2 * index + 1);//中序遍历右子树
	}
}

template <typename T>
void CMyTree_Arr<T>::posPrint(int index)
{
	if (index < vec_buff.size() && index >= 0)
	{
		posPrint(2 * index);//后序遍历左子树
		posPrint(2 * index + 1);//后序遍历右子树
		cout << vec_buff[index] << " ";//根
	}
}

template <typename T>
int CMyTree_Arr<T>::_find(T const& finaVal) const
{
	auto iter = std::find(vec_buff.begin(), vec_buff.end(), finaVal);
	if (iter != vec_buff.end())
	{
		return &*iter - &vec_buff[0];//下标
	}
	return -1;
}
/********************************************
*******************链式存储*******************
*********************************************/
template<typename T>
//树结点
struct TreeNode
{
	T data;
	TreeNode *lChild, *rChild;//左、右子节点
	TreeNode() :lChild(nullptr), rChild(nullptr){}
};

template<typename T>
class CMyTree_Node
{
	TreeNode<T> *pRoot;//根节点
public:
	CMyTree_Node();
	~CMyTree_Node();
	void clear();
	TreeNode<T> * initTree(T arr[], size_t length, int index = 0);
	void prePrint();
	void inPrint();
	void posPrint();
	void levelPrint();
private:
	void clear(TreeNode<T>*& root);//借助递归删除所有子树
	void prePrint(TreeNode<T>*& root);
	void inPrint(TreeNode<T>*& root);
	void posPrint(TreeNode<T>*& root);
	void levelPrint(TreeNode<T>*& root);
};

template <typename T>
CMyTree_Node<T>::CMyTree_Node()
{
	pRoot = nullptr;
}

template <typename T>
CMyTree_Node<T>::~CMyTree_Node()
{
	clear();
}

template <typename T>
void CMyTree_Node<T>::clear()
{
	clear(pRoot);
}

template <typename T>
TreeNode<T> * CMyTree_Node<T>::initTree(T arr[], size_t length, int index)
{
	if (index >= length)
		return nullptr;
	//前序构造
	TreeNode<T>* node = new TreeNode<T>;
	node->data = arr[index];
	node->lChild = initTree(arr, length, 2 * index + 1);
	node->rChild = initTree(arr, length, 2 * index + 2);

	pRoot = node;
	return node;
}

template <typename T>
void CMyTree_Node<T>::prePrint()
{
	prePrint(pRoot);
}

template <typename T>
void CMyTree_Node<T>::inPrint()
{
	inPrint(pRoot);
}

template <typename T>
void CMyTree_Node<T>::posPrint()
{
	posPrint(pRoot);
}

template <typename T>
void CMyTree_Node<T>::levelPrint()
{
	levelPrint(pRoot);
}

template <typename T>
void CMyTree_Node<T>::prePrint(TreeNode<T>*& root)
{
	if (root)
	{
		cout << root->data << " ";
		prePrint(root->lChild);
		prePrint(root->rChild);
	}
}

template <typename T>
void CMyTree_Node<T>::inPrint(TreeNode<T>*& root)
{
	if (root)
	{
		inPrint(root->lChild);
		cout << root->data << " ";
		inPrint(root->rChild);
	}
}

template <typename T>
void CMyTree_Node<T>::posPrint(TreeNode<T>*& root)
{
	if (root)
	{
		posPrint(root->lChild);
		posPrint(root->rChild);
		cout << root->data << " ";
	}
}

template <typename T>
void CMyTree_Node<T>::levelPrint(TreeNode<T>*& root)
{
	queue<TreeNode<T>*> *que = new queue<TreeNode<T>*>;
	root = pRoot;
	que->push(pRoot);
	while (!que->empty())
	{
		root = que->front();
		que->pop();
		cout << root->data << " ";

		if (root->lChild)
			que->push(root->lChild);
		if (root->rChild)
			que->push(root->rChild);
	}
}

template <typename T>
void CMyTree_Node<T>::clear(TreeNode<T>*& root)
{
	if (root)
	{
		clear(root->lChild);
		clear(root->rChild);
		delete root;
		root = nullptr;
	}
}

cpp

// 05binarytree.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include "MyTree.h"

int _tmain(int argc, _TCHAR* argv[])
{
	int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
	CMyTree_Arr<int>* mta = new CMyTree_Arr<int>;
	mta->initTree(arr, 10);
	bool b = mta->find(6);
	b = mta->find(11);
	mta->prePrint();
	cout << endl;
	mta->inPrint();
	cout << endl;
	mta->posPrint();
	mta->clera();
	delete mta;
	cout << endl;
	cout << "--------------------------" << endl;
	CMyTree_Node<int>* mtn = new CMyTree_Node<int>;
	mtn->initTree(arr, 10);
	mtn->prePrint();
	cout << endl;
	mtn->inPrint();
	cout << endl;
	mtn->posPrint();
	cout << endl;
	mtn->levelPrint();
	mtn->clear();
	delete mtn;
	return 0;
}

// 1 将CMyTree_Node中创建二叉树改成中序和后序
// 2 （1）不采用递归的方式来先序遍历，中序遍历 (2)判断一颗数是否是完全二叉树
//（1）和（2）二选一
//思路1 层序遍历二叉树，找到第一个非满结点 如何之后的结点还有非满结点，则不是
//思路2 讲所有结点全部压入队列，每次判断队列头为空则跳出循环 如果队列后面还有元素就不是完全二叉树