本文整理红黑树学习过程中的知识点和底层代码实现。

基本概念

1、介绍

红黑树 又叫对称二叉B树，是一种自平衡的二叉搜索树，因其插入、搜索、删除节点的效率都比较高而被广泛引用。

2、应用

1. Linux下IO多路复用epoll 的实现采用红黑树组织管理 sockfd，以支持快速的增删改查，时间复杂度为O(log(n));
2. ngnix中,用红黑树管理timer,因为红黑树是有序的,可以很快的得到距离当前最小的定时器.

3、性质

利用二叉搜索树可以简化对树中某个节点的查找，使平均情况下的时间复杂度从O(n)降到O(log(n))，但是普通的二叉搜索树在极端情况下可退化成链表，如下图：

此时的增删查效率都很低，为了应对这个问题，出现了许多加入自平衡机制的搜索树（详细可见本文最后一节），红黑树就是其中一种。

红黑树按照如下性质实现自平衡：

1. 节点是红色或者黑色；
2. 根（root）必是黑色；
3. 叶子节点都为NULL且为黑色；
4. 每个红色节点必须有两个黑色的子节点，所以保证了每个叶子节点到根节点之间的路径上不能有两个连续的红色节点；
5. 任意节点到其每个叶子节点的所有路径上都包含相同数量的黑色节点；
6. 新增加的节点为红色，因为这样效率高。

例子如下：

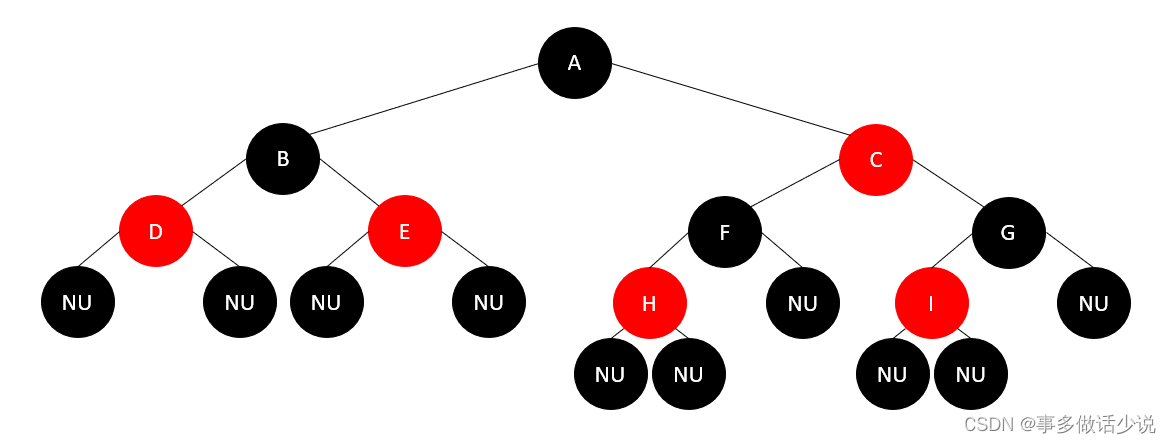
实现红黑树

1、原理

由上述红黑树的性质可推出如下性质：

从根节点到叶子节点的最长路径不大于最短路径的两倍。

最短路径：由规则5可得 只有黑色节点的路径是最短路径（整条路径上没有红色节点）
最长路径：同理，黑红相间的路径必是最长路径，此时黑色节点数量是红色节点数量+1。

通过以上性质构建出来的树即为红黑树，这些性质在进行增删查操作的过程中都会被使用到。

2、操作

在讨论红黑树增删查操作之前，先确定一些基本概念
1、树上节点关系，图片来源 b站谢某人er红黑树解说

2、插入元素节点颜色为红色，是为了更轻易修复红黑树的性质。
3、前驱：左子树中值最大的节点，后继：右子树中值最小的节点。
4、前驱和后继都是数值上最接近该节点的节点，在一些情况下需要用它们来替代删除节点（如果同时有前驱和后继，任意一个来替代删除节点都可以）。

1）查找

此过程与二叉搜索树完全一致，不再赘述，时间复杂度为O(log(n))。

2）插入

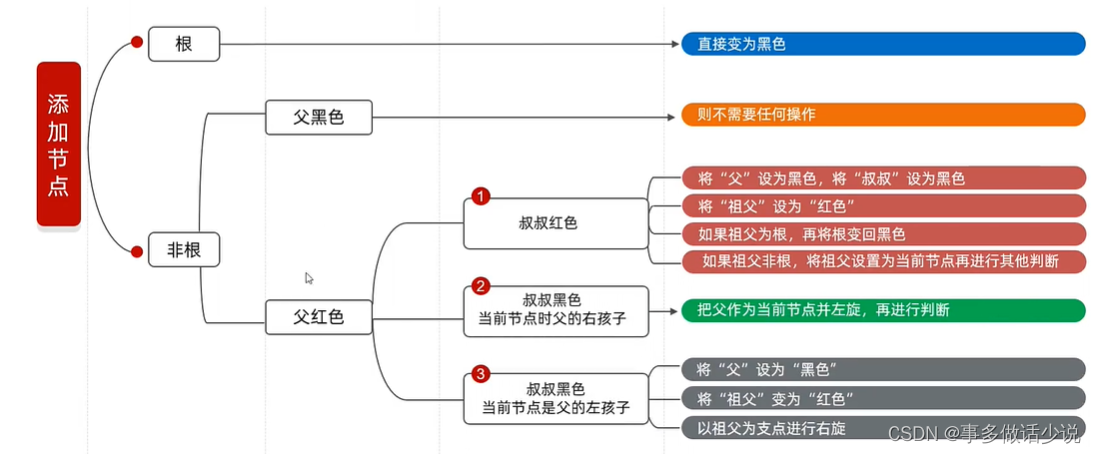
（图片来自黑马程序员视频教程）

3）删除

删除节点的工作主要分为两部分：

1. 先根据二叉搜索树的性质，找到要删除的节点；
2. 删除该节点后，修复树的红黑性质。

与删除二叉搜索树节点相同，删除红黑树节点时也只需要考虑子节点个数，但额外需要考虑被删节点的颜色。

 

情况1：被删节点无子节点，且被删节点为红色

直接删除即可，不会破坏红黑性质。

 
情况2：被删节点无子节点，且被删节点为黑色

此时删除该节点必然会破坏性质5，所以删除后通过兄弟节点及其子树（一定存在）的情况来修复红黑性质。过程比较复杂，此处不展开。详细可参考 CSDN nguliu 的博文。

情况3：被删节点有一个子节点，且被删节点为黑色

此时被删节点的子节点必为红色，此时将该节点删去，用其子节点替换被删节点即可，之后将子节点变黑即可。

情况4：被删节点有两个子节点，且被删节点为黑色或红色

先确定被删节点的前驱或者后继，然后用前驱或后继替换被删节点，删除操作完成后，会转为其他情况，然后按上述情况解决即可。

和其他相似结构的对比

1、二叉搜索树（BST）

红黑树的存在就是为了解决二叉搜索树在极端情况下会退化成链表的的问题。

在增删查的操作上。红黑树与BST相似，只是要增加一些颜色的变换以及因为颜色变换而变多的恢复情况。

2、AVL树

1）例子

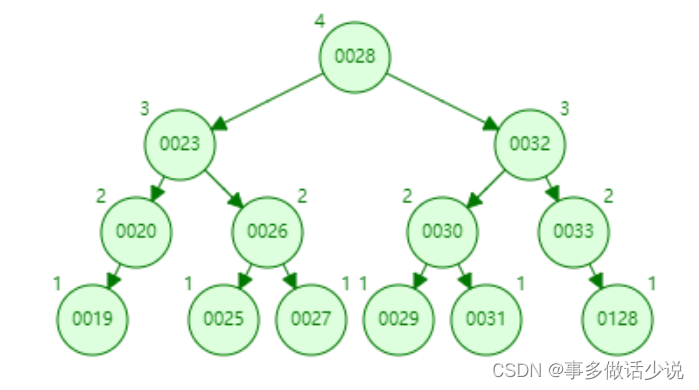
对应的相同数据的红黑树（可视化省略了叶子节点）：

2）插入

AVL利用平衡因子来使得左右子树的高度差不大于1，所以当插入元素引起树不平衡时只需要考虑旋转来平衡左右子树，并且最多只需要两次旋转就可完成，时间复杂度O(1)。

而红黑树同样也需要最多两次旋转，但还需要考虑颜色变换，时间复杂度也是O(1)。

3）删除

AVL通常需要往上回溯多个节点的节点，时间复杂度为O(log(n))。

红黑树最多只需要三次旋转，时间复杂度O(1)。

4）搜索

通过上述例子可以发现，AVL的搜索稳定性要大于红黑树（左右子树高度差一定小于等于1），而红黑树左右子树的高度差范围更大（可以等于2，此时左右子树可以相差一个黑节点和一个红节点）。

5）结论

若业务需要大量的插入和删除（例如epoll中的sockfd），红黑树效率更高，如果删除操作较少，AVL效率更高。