DQN算法详解

一.概述

概括来说，RL要解决的问题是：让agent学习在一个环境中的如何行为动作(act)， 从而获得最大的奖励值总和(total reward)。
这个奖励值一般与agent定义的任务目标关联。
agent需要的主要学习内容：第一是行为策略(action policy)， 第二是规划(planning)。
其中，行为策略的学习目标是最优策略， 也就是使用这样的策略，可以让agent在特定环境中的行为获得最大的奖励值，从而实现其任务目标。

行为(action)可以简单分为：

• 连续的：如赛 车游戏中的方向盘角度、油门、刹车控制信号，机器人的关节伺服电机控制信号。
• 离散的：如围棋、贪吃蛇游戏。 Alpha Go就是一个典型的离散行为agent。

DDPG是针对连续行为的策略学习方法。

二.DDPG的定义和应用场景

在RL领域，DDPG主要从：PG -> DPG -> DDPG 发展而来。

基本概念：

PG

R.Sutton 在2000年提出的Policy Gradient 方法，是RL中，学习连续的行为控制策略的经典方法，其提出的解决方案是：
通过一个概率分布函数 ， 来表示每一步的最优策略， 在每一步根据该概率分布进行action采样，获得当前的最佳action取值；即：

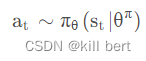
生成action的过程，本质上是一个随机过程；最后学习到的策略，也是一个随机策略(stochastic policy).

DPG

Deepmind的D.Silver等在2014年提出DPG： Deterministic Policy Gradient， 即确定性的行为策略，每一步的行为通过函数μ 直接获得确定的值：

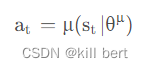
这个函数μ即最优行为策略，不再是一个需要采样的随机策略。

为何需要确定性的策略？简单来说，PG方法有以下缺陷：

1. 即使通过PG学习得到了随机策略之后，在每一步行为时，我们还需要对得到的最优策略概率分布进行采样，才能获得action的具体值；而action通常是高维的向量，比如25维、50维，在高维的action空间的频繁采样，无疑是很耗费计算能力的；
2. 在PG的学习过程中，每一步计算policy gradient都需要在整个action space进行积分:
   

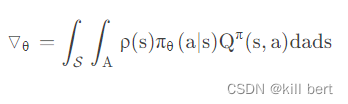
DDPG

Deepmind在2016年提出DDPG，全称是：Deep Deterministic Policy Gradient,是将深度学习神经网络融合进DPG的策略学习方法。
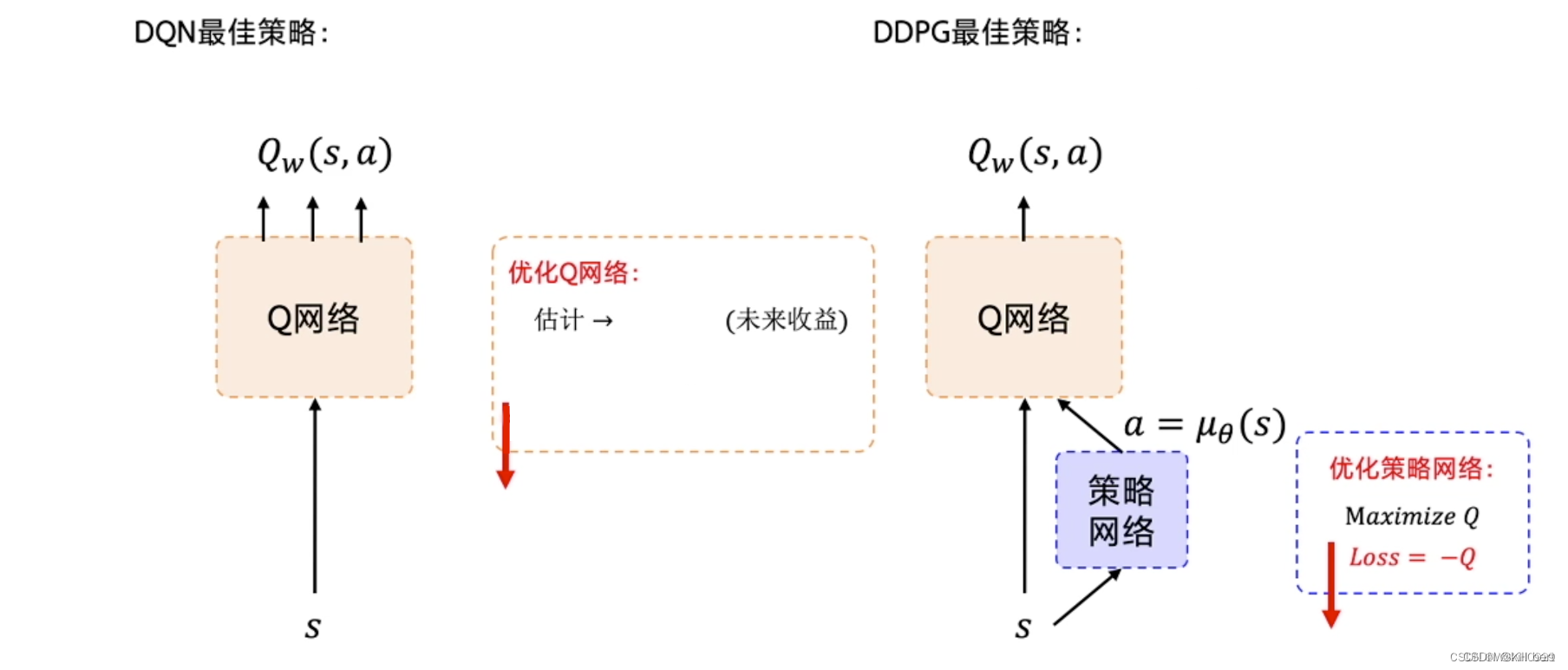
相对于DPG的核心改进是： 采用卷积神经网络作为策略函数μ 和Q 函数的模拟，即策略网络和Q网络；然后使用深度学习的方法来训练上述神经网络。

Q函数的实现和训练方法，采用了Deepmind 2015年发表的DQN方法 ,即 Alpha Go使用的Q函数方法。

1.DDQN解决问题方法

1. 使用卷积神经网络来模拟策略函数和Q函数，并用深度学习的方法来训练，证明了在RL方法中，非线性模拟函数的准确性和高性能、可收敛；
   而DPG中，可以看成使用线性回归的机器学习方法：使用带参数的线性函数来模拟策略函数和Q函数，然后使用线性回归的方法进行训练。
2. experience replay memory的使用：actor同环境交互时，产生的transition数据序列是在时间上高度关联(correlated)的，如果这些数据序列直接用于训练，会导致神经网络的overfit，不易收敛。
   DDPG的actor将transition数据先存入experience replay buffer, 然后在训练时，从experience replay buffer中随机采样mini-batch数据，这样采样得到的数据可以认为是无关联的。
3. target 网络和online 网络的使用， 使的学习过程更加稳定，收敛更有保障。
   

四、 代码详解

import gym
import paddle
import paddle.nn as nn
from itertools import count
from paddle.distribution import Normal
import numpy as np
from collections import deque
import random
import paddle.nn.functional as F
# 定义评论家网络结构
# DDPG这种方法与Q学习紧密相关，可以看作是连续动作空间的深度Q学习。
class Critic(nn.Layer):
    def __init__(self):
        super(Critic, self).__init__()
        self.fc1 = nn.Linear(3, 256)
        self.fc2 = nn.Linear(256 + 1, 128)
        self.fc3 = nn.Linear(128, 1)
        self.relu = nn.ReLU()

    def forward(self, x, a):
        x = self.relu(self.fc1(x))
        x = paddle.concat((x, a), axis=1)
        x = self.relu(self.fc2(x))
        x = self.fc3(x)
        return x

# 定义演员网络结构
# 为了使DDPG策略更好地进行探索，在训练时对其行为增加了干扰。 原始DDPG论文的作者建议使用时间相关的 OU噪声 ，
# 但最近的结果表明，不相关的均值零高斯噪声效果很好。 由于后者更简单，因此是首选。
class Actor(nn.Layer):
    def __init__(self, is_train=True):
        super(Actor, self).__init__()
        self.fc1 = nn.Linear(3, 256)
        self.fc2 = nn.Linear(256, 128)
        self.fc3 = nn.Linear(128, 1)
        self.relu = nn.ReLU()
        self.tanh = nn.Tanh()
        self.noisy = Normal(0, 0.2)
        self.is_train = is_train

    def forward(self, x):
        x = self.relu(self.fc1(x))
        x = self.relu(self.fc2(x))
        x = self.tanh(self.fc3(x))
        return x

    def select_action(self, epsilon, state):
        state = paddle.to_tensor(state,dtype="float32").unsqueeze(0)
        with paddle.no_grad():
            action = self.forward(state).squeeze() + self.is_train * epsilon * self.noisy.sample([1]).squeeze(0)
        return 2 * paddle.clip(action, -1, 1).numpy()

# 重播缓冲区:这是智能体以前的经验， 为了使算法具有稳定的行为，重播缓冲区应该足够大以包含广泛的体验。
# 如果仅使用最新数据，则可能会过分拟合，如果使用过多的经验，则可能会减慢模型的学习速度。 这可能需要一些调整才能正确。
class Memory(object):
    def __init__(self, memory_size: int) -> None:
        self.memory_size = memory_size
        self.buffer = deque(maxlen=self.memory_size)

    def add(self, experience) -> None:
        self.buffer.append(experience)

    def size(self):
        return len(self.buffer)

    def sample(self, batch_size: int, continuous: bool = True):
        if batch_size > len(self.buffer):
            batch_size = len(self.buffer)
        if continuous:
            rand = random.randint(0, len(self.buffer) - batch_size)
            return [self.buffer[i] for i in range(rand, rand + batch_size)]
        else:
            indexes = np.random.choice(np.arange(len(self.buffer)), size=batch_size, replace=False)
            return [self.buffer[i] for i in indexes]

    def clear(self):
        self.buffer.clear()


# 定义软更新的函数
def soft_update(target, source, tau):
    for target_param, param in zip(target.parameters(), source.parameters()):
        target_param.set_value(target_param * (1.0 - tau) + param * tau)

    # 定义环境、实例化模型


env = gym.make('Pendulum-v1')
actor = Actor()
critic = Critic()
actor_target = Actor()
critic_target = Critic()

# 定义优化器
critic_optim = paddle.optimizer.Adam(parameters=critic.parameters(), learning_rate=3e-5)
actor_optim = paddle.optimizer.Adam(parameters=actor.parameters(), learning_rate=1e-5)

# 定义超参数
explore = 50000
epsilon = 1
gamma = 0.99
tau = 0.001

memory_replay = Memory(50000)
begin_train = False
batch_size = 32

learn_steps = 0

#writer = LogWriter('logs')

# 训练循环
for epoch in count():
    state = env.reset()
    episode_reward = 0
    for time_step in range(200):
        action = actor.select_action(epsilon, state)
        next_state, reward, done, _ = env.step([action])
        episode_reward += reward
        reward = (reward + 8.1) / 8.1
        memory_replay.add((state, next_state, action, reward))
        if memory_replay.size() > 1280:

            learn_steps += 1
            if not begin_train:
                print('train begin!')
                begin_train = True
            experiences = memory_replay.sample(batch_size, False)
            batch_state, batch_next_state, batch_action, batch_reward = zip(*experiences)

            batch_state = paddle.to_tensor(batch_state, dtype="float32")
            batch_next_state = paddle.to_tensor(batch_next_state, dtype="float32")
            batch_action = paddle.to_tensor(batch_action, dtype="float32").unsqueeze(1)
            batch_reward = paddle.to_tensor(batch_reward, dtype="float32").unsqueeze(1)

            # 均方误差 y - Q(s, a) ， y是目标网络所看到的预期收益， 而 Q(s, a)是Critic网络预测的操作值。
            # y是一个移动的目标，评论者模型试图实现的目标；这个目标通过缓慢的更新目标模型来保持稳定。
            with paddle.no_grad():
                Q_next = critic_target(batch_next_state, actor_target(batch_next_state))
                Q_target = batch_reward + gamma * Q_next

            critic_loss = F.mse_loss(critic(batch_state, batch_action), Q_target)

            critic_optim.clear_grad()
            critic_loss.backward()
            critic_optim.step()

            #writer.add_scalar('critic loss', critic_loss.numpy(), learn_steps)
            # 使用Critic网络给定值的平均值来评价Actor网络采取的行动。 我们力求使这一数值最大化。
            # 因此，我们更新了Actor网络，对于一个给定状态，它产生的动作尽量让Critic网络给出高的评分。
            critic.eval()
            actor_loss = - critic(batch_state, actor(batch_state))
            # print(actor_loss.shape)
            actor_loss = actor_loss.mean()
            actor_optim.clear_grad()
            actor_loss.backward()
            actor_optim.step()
            critic.train()
            #writer.add_scalar('actor loss', actor_loss.numpy(), learn_steps)

            soft_update(actor_target, actor, tau)
            soft_update(critic_target, critic, tau)
            env.render()
        if epsilon > 0:
            epsilon -= 1 / explore
        state = next_state

    #writer.add_scalar('episode reward', episode_reward, epoch)
    if epoch % 10 == 0:
        print('Epoch:{}, episode reward is {}'.format(epoch, episode_reward))

    if epoch % 200 == 0:
        paddle.save(actor.state_dict(), 'model/ddpg-actor' + str(epoch) + '.para')
        paddle.save(critic.state_dict(), 'model/ddpg-critic' + str(epoch) + '.para')
        print('model saved!')