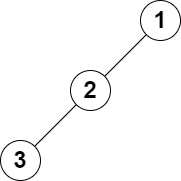
回溯法（back tracking）（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回到上一步，重新选择，这种走不通就退回再走的技术为回溯法。

回溯法常常应用于求解组合优化问题，如八皇后问题、0-1背包问题、图的着色问题等。在求解这些问题时，回溯法可以枚举所有可能的解，并通过剪枝来避免搜索无效的解，从而提高搜索效率。

回溯法的实现通常采用递归的方式，在递归的过程中，需要记录当前搜索的状态，以及已经搜索过的路径和结果，同时也需要注意回溯时状态的恢复。

尽管回溯法在解决某些问题上非常有效，但是在某些情况下它的复杂度可能非常高，甚至会超出实际可行的范围。因此，在应用回溯法求解问题时，需要仔细评估问题的规模和复杂度，并采取合适的优化措施来提高效率。

回溯法的优点：

1.适用范围广：回溯法可以解决很多复杂的问题，如八皇后问题、数独、迷宫等。

2.通用性强：回溯法不依赖于特定问题的解法，只需要定义问题的状态和可行解的条件，就能应用到各种问题中。

3.解法唯一：回溯法可以保证找到所有符合要求的解，并且找到的解法是唯一的。

回溯法的缺点：

1.时间复杂度高：回溯法需要搜索所有可能的解，因此时间复杂度很高。在面对大规模问题时，运行时间很长。

2.空间复杂度高：回溯法需要存储所有的状态，因此空间复杂度很高。在面对大规模问题时，占用的空间很大。

3.搜索范围大：回溯法会搜索所有可能的解，因此搜索范围很大。在面对复杂问题时，可能需要搜索很多次才能找到解法。

================================

几乎任何事情都是越做越简单，越想越困难，越拖着越想放弃。
——稻盛和夫