众所周知，信息和信息处理的完全量子理论提供了诸多好处，其中包括一种基于基础物理的安全密码学，以及一种实现量子计算机的合理希望，这种计算机可以加速某些数学问题的解决。这些好处来自于独特的量子特性，如叠加、纠缠和非定域性，这些特性在经典力学中不存在。在过去的四十年里，许多重要的量子信息处理协议被提出，包括量子密钥分发(QKD)、量子隐形传态、量子因数分解算法和Grover搜索算法。量子密码学是量子信息处理中最成功的应用之一，因为物理定律保证了其固有的安全性。相反，经典密码学通常依赖于计算复杂性的假设。第一种量子密码系统是量子密钥分发，用于生成仅由两方共享的随机密钥。后来，量子密码学得到了广泛的研究，并提出了许多协议。同态加密(HE)方案允许在不事先解密的情况下处理加密数据。这个有用的功能已经存在了30多年。2009年，Craig Gentry引入了第一个可信且可实现的完全同态加密(FHE)方案，该方案支持在加密数据上处理任何函数。但该方案只能实现计算安全性。人们自然会问，量子力学的物理原理是否可以应用于构建HE方案，从而实现更好的安全性/性能。答案是肯定的，并且已经提出了各种量子同态加密(QHE)方案。综上所述，这些方案可分为两类。一种是有效的信息理论安全(ITS)，只能评估所有可能函数的子集;另一种只能实现计算安全性。此外，已有研究表明，用ITS构建高效量子FHE是不可能的。最近，Dor Bitan等人利用一组特定的随机碱基，提出了一种量子同态加密方案。它可以加密和外包经典数据的存储，同时使用ITS对加密数据进行量子门计算。

秘密共享与量子同态加密数学基础

同态加密(HE)方案可以用密钥生成(Gen)、加密(Enc)、求值(Eval)和解密(Dec)四种算法的集合来描述。下面我们简要回顾一下同态随机基加密方案。
密钥生成：从[0,2π]×{π/2，−π/2}中输出一个一致随机对(θ，φ)的密钥。
加密：输出由|q> = K|b>获得的量子比特|q，输入消息b∈{0,1}，密钥K = (θ， φ)。这里K是加密运算符的形式

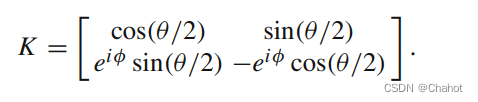
解密：输出输入|q>的明文，密钥k = (θ， φ)。可以通过对|q>施加K^†，并在计算基中输出K^†|q>的测量值来实现。

它支持X门、CNOT门和D门(用于创建贝尔状态)的同态求值，其中控制量子位位于计算基中。在这里，我们重点讨论了本文中出现的X门和CNOT门。对于X门，我们可以令|ψ0> =K |0>， |ψ1> =K |1>，得到

$$X|{\psi }_0⟩=\pm i|{\psi }_1⟩,X|{\psi }_1⟩=\mp i|{\psi }_0⟩$$

对于计算基中有控制量子比特的CNOT门，我们可以验证这一点
$$CNOT|1⟩\otimes |{\psi }_0⟩=\pm i|1⟩\otimes |{\psi }_1⟩,CNOT|1⟩\otimes |{\psi }_1⟩=\mp i|1⟩\otimes |{\psi }_0⟩$$

由于±i(∓i)是一个整体相，我们可以在测量量子态时去掉它。

秘密共享

本节介绍了Shamir提出的阈值为(t, n)的秘密共享方案。在该方案中，它展示了如何将秘密s分成n个片段，使得任何t个片段都可以很容易地恢复s，但即使完全知道t - 1个片段，也不会泄露任何关于s的信息。该方案包括两个算法:

发起者D选择一个t - 1次的随机多项式f (x):$f(x)=a_0+a_1+...+a_{t-1}{x}^{t-1}modp$，秘密$s=a_0$。$a_0,a_1,\dots ，$在有限域F中，p是素数。然后D计算:$s_j=f(x_j)，j=1,2,...$，其中x_j为当事人P_j的公开信息。最后，该算法输出一个包含n个共享(s1,s2，…，sn)的列表，并将每个共享s_j安全地分配给P_j。
秘密重构取任意m (m≥t)个组成部分s_j, j∈U = {i₁,i₂，…，i_m}， U规模{1,2，…， n}作为输入和输出秘密s，可以得出下式
$$s=\sum _{j\in U}{c}_j=\sum _{j\in U}f(x_j)\prod _{r\in U，r\ne j}\frac{x_r}{x_r-x_j}modp$$