《PyTorch 深度学习实践》第9讲多分类问题(Kaggle作业：otto分类)

文章目录

- 1 一些细碎代码
- - 1.1 Cross Entropy
  - 1.2 Mini-batch: batch_size=3
- 2 示例
- 3 作业
- - 任务描述
  - 查看数据
  - 进行建模
  - 提交Kaggle
  - 总结

该专栏内容为对该视频的学习记录：【《PyTorch深度学习实践》完结合集】
专栏的全部代码、数据集和课件全放在个人GitHub了，欢迎自取。

1 一些细碎代码

1.1 Cross Entropy

一个样本的交叉熵，使用numpy实现：

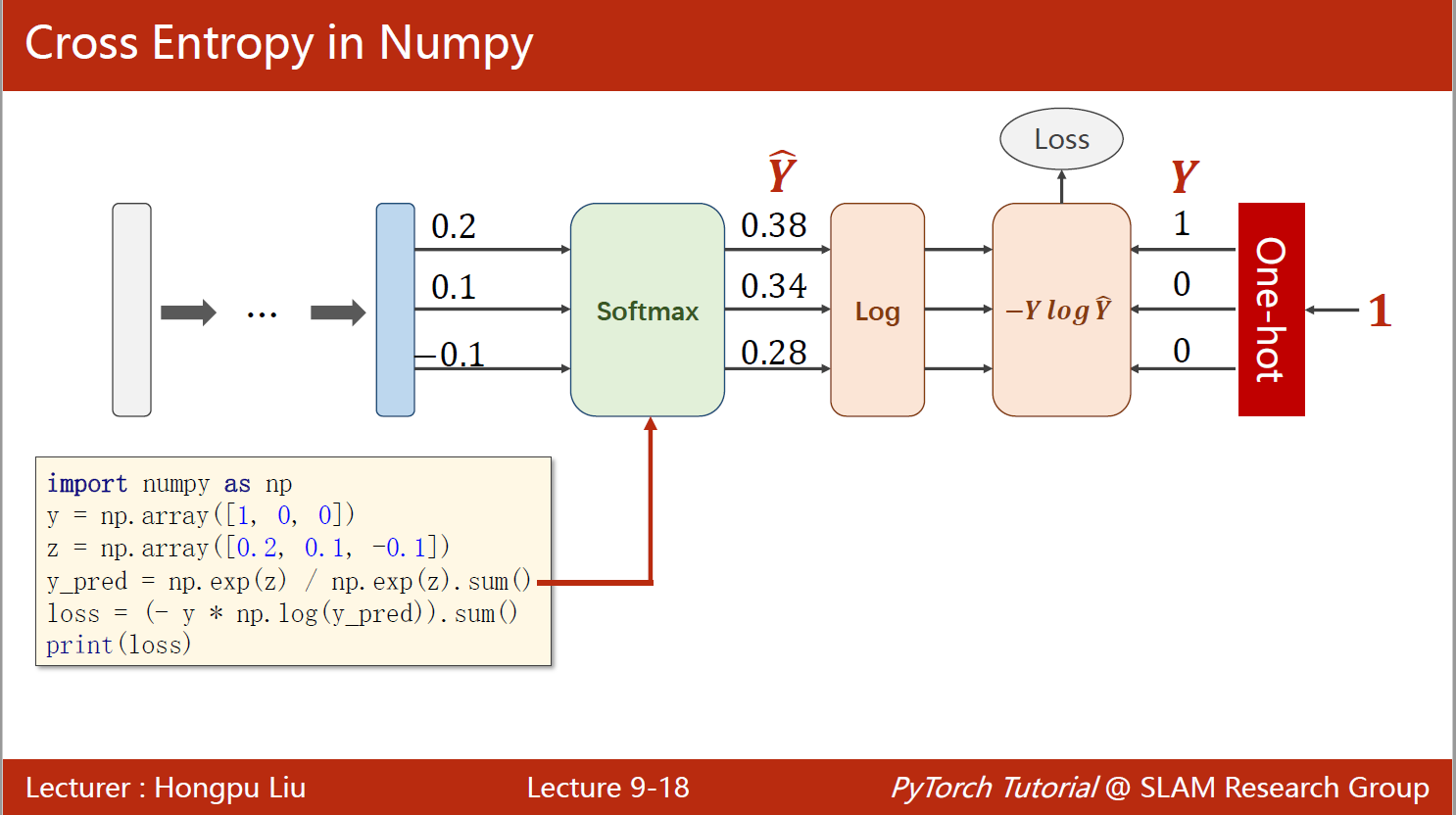
import numpy as np

y = np.array([1, 0, 0])  # one-hot编码，该样本属于第一类
z = np.array([0.2, 0.1, -0.1])  # 线性输出
y_pred = np.exp(z) / np.exp(z).sum()  # 经softmax处理
loss = (-y * np.log(y_pred)).sum()
print(loss, y_pred)

0.9729189131256584 [0.37797814 0.34200877 0.28001309]

同样一个样本的交叉熵，使用torch实现:

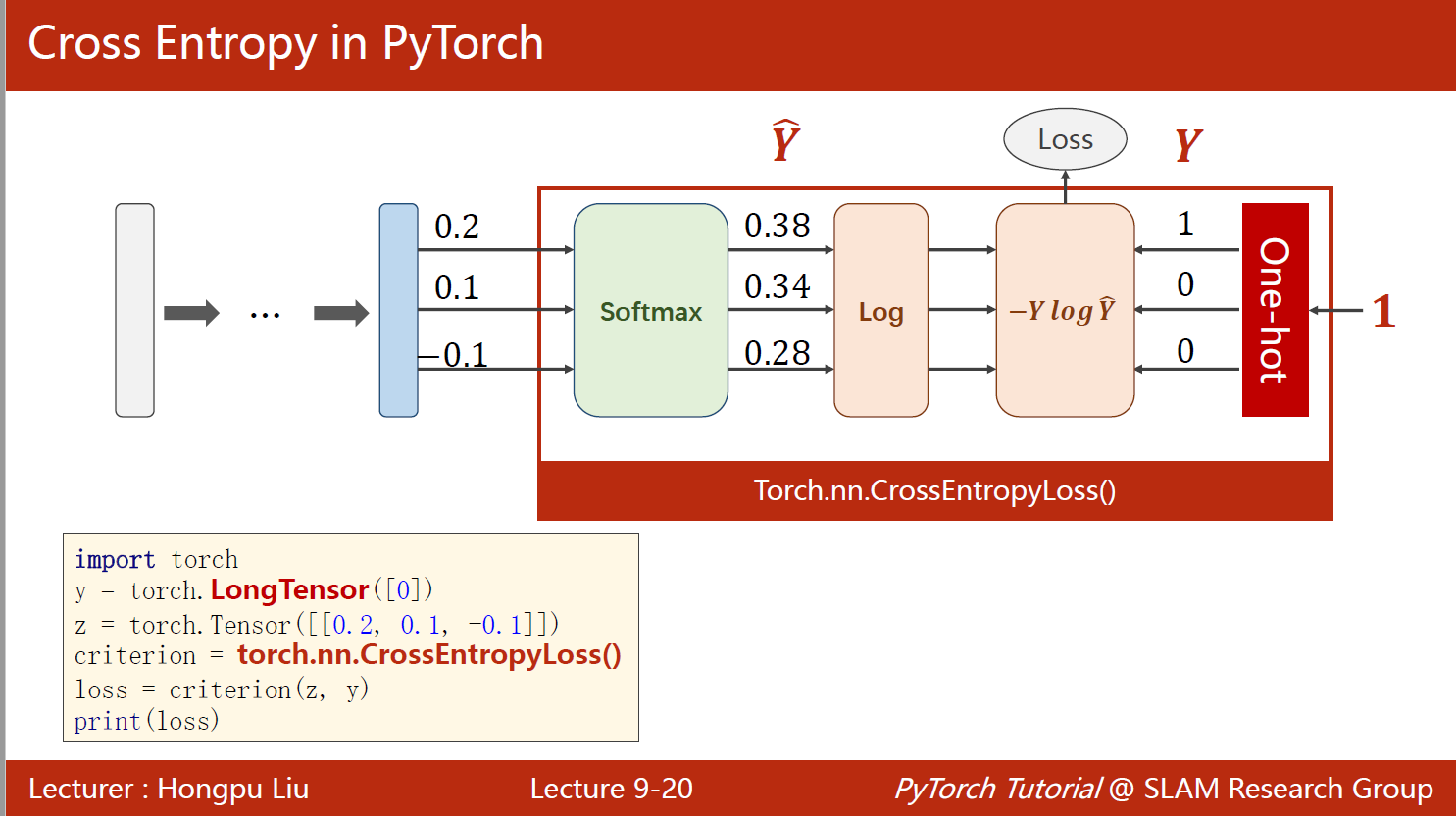
import torch

y = torch.LongTensor([0])  # 该样本属于第一类
z = torch.tensor([[0.2, 0.1, -0.1]])  # 线性输出
criterion = torch.nn.CrossEntropyLoss()  # 使用交叉熵损失
loss = criterion(z, y)
print(loss)

tensor(0.9729)

1.2 Mini-batch: batch_size=3

import torch

criterion = torch.nn.CrossEntropyLoss()
Y = torch.LongTensor([2, 0, 1])  #这里有三个样本，每个样本的类别分别为2,0,1
# 第一种预测的线性输出，并不是概率。跟上面的z一样，只是这里有三个样本
Y_pred1 = torch.Tensor([[0.1, 0.2, 0.9],  # 2
                        [1.1, 0.1, 0.2],  # 0
                        [0.2, 2.1, 0.1]])  # 1
# 第二种预测的线性输出
Y_pred2 = torch.Tensor([[0.8, 0.2, 0.3],  # 0
                        [0.2, 0.3, 0.5],  # 2
                        [0.2, 0.2, 0.5]])  # 2

l1 = criterion(Y_pred1, Y)
l2 = criterion(Y_pred2, Y)
print("Batch Loss1=", l1.item(), "\nBatch Loss2=", l2.item())

Batch Loss1= 0.4966353178024292 
Batch Loss2= 1.2388995885849

2 示例

这是一个使用PyTorch实现的简单的神经网络模型，用于对MNIST手写数字进行分类。代码主要包含以下几个部分：

数据准备：使用PyTorch的DataLoader加载MNIST数据集，对数据进行预处理，如将图片转为Tensor，并进行标准化。
模型设计：设计一个包含5个线性层和ReLU激活函数的神经网络模型，最后一层输出10个类别的概率分布。
损失和优化器：定义交叉熵损失函数和SGD优化器，用于训练模型。
训练和测试：使用训练数据对模型进行训练，使用测试数据对模型进行测试，输出准确率。

在训练过程中，每300个batch打印一次平均loss；在测试过程中，使用with torch.no_grad()上下文管理器关闭梯度计算，以提高测试效率。最终输出模型在测试集上的准确率。在该模型中，准确率最高为97%

import torch
import torch.nn.functional as F
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader

# 1、准备数据集
batch_size = 64
transform = transforms.Compose([  # 一系列的操作，Compose将其组合在一起
    transforms.ToTensor(),  # 将图片转为Tensor，并且转换为CHW，即C*H*W，C为通道数，H为高，W为宽，这里为1*28*28
    transforms.Normalize((0.1307,), (0.3081,))  # 标准化到[0,1]，均值和方差
])
train_dataset = datasets.MNIST(root='../P6 逻辑斯谛回归/data',
                               train=True,
                               download=False,  # 在P6 逻辑斯谛回归中我已下载，这里直接读取即可
                               transform=transform)
test_dataset = datasets.MNIST(root='../P6 逻辑斯谛回归/data',
                              train=False,
                              download=False,
                              transform=transform)
train_loader = DataLoader(dataset=train_dataset,
                          batch_size=batch_size,
                          shuffle=True)
test_loader = DataLoader(dataset=test_dataset,
                         batch_size=batch_size,
                         shuffle=False)  # 测试集设置为False，方便观察结果


# 2、设计模型
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = torch.nn.Linear(28 * 28, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)

    def forward(self, x):
        x = x.view(-1, 28 * 28)  # 将图片展开为一维向量
        x = F.relu(self.l1(x))  # 激活函数
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x)  # 最后一层不需要激活函数，因为交叉熵损失函数会对其进行处理


model = Net()

# 3、构建损失和优化器
criterion = torch.nn.CrossEntropyLoss()  # 交叉熵损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 优化器,lr为学习率，momentum为动量


# 4、训练和测试
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, labels = data
        optimizer.zero_grad()  # 梯度清零
        # forward + backward + update
        outputs = model(inputs)  # outputs并不是概率，而是线性层的输出，但其大小顺序与概率分布相同
        loss = criterion(outputs, labels)
        loss.backward()  # 反向传播
        optimizer.step()  # 更新参数

        running_loss += loss.item()
        if batch_idx % 300 == 299:  # 每300个batch打印一次平均loss
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0
    total = 0
    with torch.no_grad():  # 测试过程中不需要计算梯度
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)  # 返回每一行中最大值的那个元素，以及其索引
            total += labels.size(0)  # labels的size为[64]，即64个样本
            correct += (predicted == labels).sum().item()  # 统计预测正确的样本个数
    print('Accuracy on test set: %d %%' % (100 * correct / total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

[1,   300] loss: 2.166
[1,   600] loss: 0.767
[1,   900] loss: 0.385
Accuracy on test set: 90 %
[2,   300] loss: 0.307
[2,   600] loss: 0.262
[2,   900] loss: 0.232
Accuracy on test set: 93 %
[3,   300] loss: 0.192
[3,   600] loss: 0.164
[3,   900] loss: 0.159
Accuracy on test set: 95 %
[4,   300] loss: 0.133
[4,   600] loss: 0.118
[4,   900] loss: 0.119
Accuracy on test set: 96 %
[5,   300] loss: 0.100
[5,   600] loss: 0.094
[5,   900] loss: 0.094
Accuracy on test set: 97 %
[6,   300] loss: 0.074
[6,   600] loss: 0.078
[6,   900] loss: 0.074
Accuracy on test set: 97 %
[7,   300] loss: 0.062
[7,   600] loss: 0.060
[7,   900] loss: 0.058
Accuracy on test set: 97 %
[8,   300] loss: 0.048
[8,   600] loss: 0.049
[8,   900] loss: 0.050
Accuracy on test set: 97 %
[9,   300] loss: 0.040
[9,   600] loss: 0.040
[9,   900] loss: 0.041
Accuracy on test set: 97 %
[10,   300] loss: 0.033
[10,   600] loss: 0.032
[10,   900] loss: 0.032
Accuracy on test set: 97 %

3 作业

任务描述

Otto Group 是全球最大的电子商务公司之一，在 20 多个国家/地区设有子公司，包括 Crate & Barrel（美国）、Otto.de（德国）和 3 Suisses（法国）。我们每天在全球销售数百万种产品，并且有数千种产品被添加到我们的产品线中。

对我们产品的性能进行一致的分析至关重要。然而，由于我们多样化的全球基础设施，许多相同的产品会得到不同的分类。因此，我们产品分析的质量在很大程度上取决于对相似产品进行准确聚类的能力。分类越好，我们对产品系列的洞察力就越多。

对于本次比赛，我们提供了一个包含 200,000 多种产品的 93 个特征的数据集。目标是建立一个能够区分我们主要产品类别的预测模型。

查看数据

# 导入相关库
import numpy as np
import pandas as pd
import torch
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader

# 先了解一下数据的基本情况，再进行我们后面的建模流程
data = pd.read_csv('../Data/otto/train.csv')
data.head()  #查看前五行
data.info()  #查看数据信息
data.describe()  #查看数据统计信息
data.isnull().sum()  #查看缺失值
data['target'].value_counts()  #查看各个类别的数量

数据信息：完整的数据集包含 93 个特征和1 个目标变量。目标变量是一个类别变量，包含 9 个类别。每个类别的数量都不相同，但是每个类别的数量都超过 10,000 个。数据集中没有缺失值。

进行建模

# 1、准备数据
class OttoDataset(Dataset):
    def __init__(self):
        xy = np.loadtxt('../Data/otto/train.csv', delimiter=',', skiprows=1, usecols=np.arange(1, 94))
        df = pd.read_csv('../Data/otto/train.csv', sep=',')
        df['target'] = df['target'].map({'Class_1': 1, 'Class_2': 2,  #通过映射将类别转换为数字
                                         'Class_3': 3, 'Class_4': 4,
                                         'Class_5': 5, 'Class_6': 6,
                                         'Class_7': 7, 'Class_8': 8,
                                         'Class_9': 9})
        df['target'] = df['target'].astype('float')
        self.len = xy.shape[0]
        self.x_data = torch.from_numpy(xy[:, :])
        self.y_data = torch.tensor(df['target'].values)

    def __getitem__(self, index):
        return self.x_data[index], self.y_data[index]

    def __len__(self):
        return self.len


dataset = OttoDataset()
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True)


# 2、构建模型
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = torch.nn.Linear(93, 64)
        self.l2 = torch.nn.Linear(64, 32)
        self.l3 = torch.nn.Linear(32, 16)
        self.l4 = torch.nn.Linear(16, 9)

    def forward(self, x):
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        return self.l4(x)


model = Net()

# 3、构建损失和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.05, momentum=0.5)


# 4、训练模型
def train(epoch):
    model.train()  #开启训练模式
    running_loss = 0.0
    for batch_idx, (inputs, labels) in enumerate(train_loader):
        inputs, labels = inputs.float(), labels.long()
        optimizer.zero_grad()
        # forward + backward + update
        outputs = model(inputs)  # 是线性层的输出值，不是概率值
        loss = criterion(outputs, labels - 1)  #因为类别是从1开始的，所以要减1
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
        if (epoch % 5 == 0) and batch_idx % 1000 == 999:
            print('[%d, %5d] loss: %.3f' % (epoch, batch_idx + 1, running_loss / 1000))
            running_loss = 0.0


# 5、进行预测并保存结果
def test():
    model.eval()  # 开启测试模式
    xyTest = np.loadtxt('../Data/otto/test.csv', delimiter=',', skiprows=1, usecols=np.arange(1, 94))
    df1 = pd.read_csv('../Data/otto/test.csv', sep=',')
    xy_pred = torch.from_numpy(xyTest[:, :])  # 将测试集转换为tensor
    column_list = ['id', 'Class_1', 'Class_2', 'Class_3', 'Class_4', 'Class_5',
                   'Class_6', 'Class_7', 'Class_8', 'Class_9']
    d = pd.DataFrame(0, index=np.arange(xy_pred.shape[0]), columns=column_list)  # 创建一个空的DataFrame
    d.iloc[:, 1:] = d.iloc[:, 1:].astype('float')
    d['id'] = df1['id']  # 将id列赋值

    output = model(xy_pred.clone().detach().requires_grad_(True).float())
    row = F.softmax(output, dim=1).data  # 将输出值转换为概率值。注意维度为1
    classes = row.numpy()  # 将tensor转换为numpy
    classes = np.around(classes, decimals=2)  # 保留两位小数
    d.iloc[:, 1:] = classes  # 将概率值赋值给DataFrame
    d.to_csv('Submission.csv', index=False)  # 保存结果


if __name__ == '__main__':
    for epoch in range(1, 30):
        train(epoch)
    test()

[5,  1000] loss: 0.537
[10,  1000] loss: 0.497
[15,  1000] loss: 0.480
[20,  1000] loss: 0.462
[25,  1000] loss: 0.447

提交Kaggle

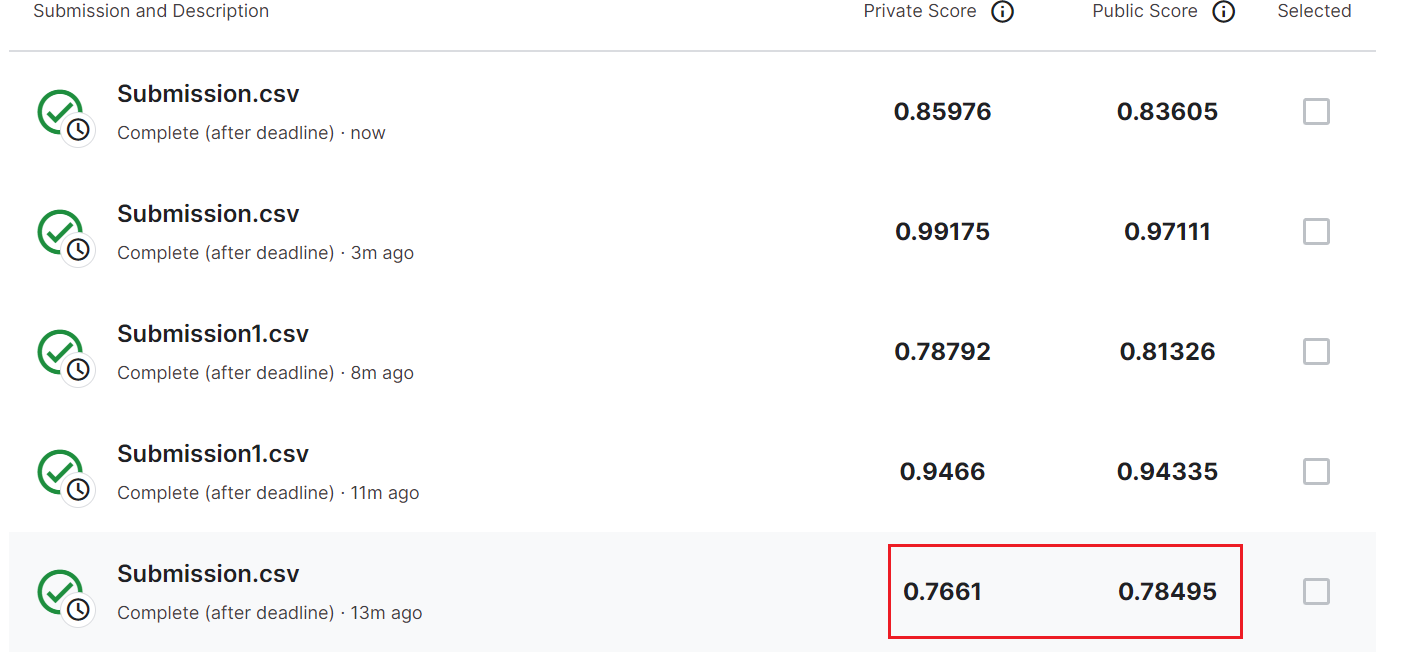
这个评判标准好像是两列的分数越低越好，可以看见我试了好多次，最低就只到0.7661了，累人~

总结

该代码是一个简单的 PyTorch 神经网络模型，用于分类 Otto 数据集中的产品。这个数据集包含来自九个不同类别的93个特征，共计约60,000个产品。

代码的执行分为以下几个步骤：

1.数据准备：首先读取 Otto 数据集，然后将类别映射为数字，将数据集划分为输入数据和标签数据，最后使用 PyTorch 中的 DataLoader 将数据集分成多个小批量。

2.构建模型：构建了一个简单的四层全连接神经网络，输入层有93个特征，输出层有9个类别。

3.构建损失和优化器：选择了交叉熵损失作为损失函数，使用随机梯度下降算法作为优化器。

4.训练模型：每次迭代一个 epoch，使用小批量数据进行训练，输出训练的损失值，直到训练完所有的 epoch。

5.进行预测并保存结果：使用模型进行预测并保存结果到本地文件。

该代码使用 PyTorch 库中的张量 (Tensor) 和自动微分 (autograd) 来实现反向传播算法，这些功能使得神经网络的实现更加简单和高效。