2.9 积分模块（2）

External reset:

在什么条件下进行外部重置操作描述一下每个选项：

• Rising：当重置信号从非正的值（0或负值）变为正值时，重置积分器的状态。

• Falling：当重置信号从正值变为非正值（0或负值）时，重置积分器的状态。

• Either：当重置信号变化时（从0到非0或从非0到0），或者在符号变化时（从正数到负数或反之），重置积分器的状态。

• Level：当重置信号在当前时间步为非0，或者在前一个时间步为非0而在当前时间步变为0时，重置积分器的状态。

• Level-Hold：当重置信号在当前时间步为非0时，进入重置状态并持续一段时间，然后恢复到普通积分状态。

在某些建模方案中，使用 State port 可以避免创建代数环。

代数环指的是在 Simulink 模型中，当一个变量的输出值需要反馈到所在模块的输入中时，就会形成一个环路的情况。因为这种情况涉及到对变量自身进行连续时间域的解算，通常需要无限次迭代计算才能得到正确的结果，这会导致模型无法正常运行并进入死循环。代数环通常是模型设计中不希望出现的情况，一旦出现，可能会导致模型计算时间过长，模型无法正常运行等问题。因此，在设计模型时，需要仔细确认是否出现代数环。

2.10 单位延迟模块

广泛用于：迭代式滤波器，非迭代式滤波器，离散时间传递函数控制系统

2.11 离散时间积分模块

1）Forward Euler method:

y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n-1)

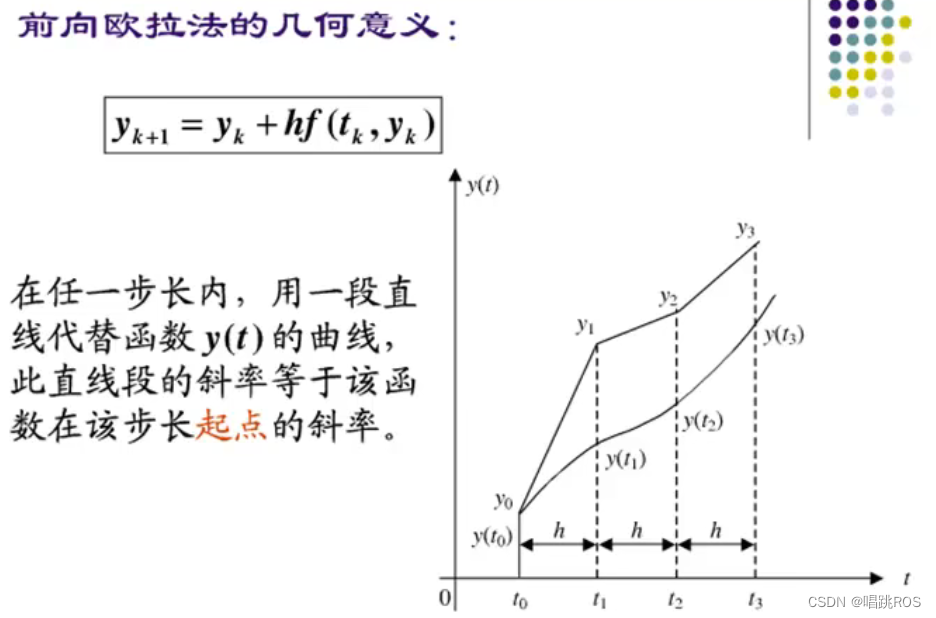
前向欧拉法是最简单的一种数值解微分方程的方法。

假设需要求解如下一阶常微分方程：
y'(t) = f(t,y(t))，t ∈ [t0, T]，y(t0) = y0
其中，y(t) 表示未知函数，f(t,y) 表示函数 f 的导数。该方程的物理意义是，y‘(t) 是在时间 t 上 y(t) 的变化率，即在 t 时刻的瞬时斜率。
假设有一组离散时间点 {tn}，其步长为 h，即 tn+1 = tn + h，以及一组数值解 {yn}，则前向欧拉法的递推公式为：
yn+1 = yn + h * f(tn, yn)
即利用函数值在当前时刻（tn，yn）和导数在此时刻的近似值（f(tn,yn)），计算出 yn+1，即下一个时间点的函数值的估计值。

下面是一个通过前向欧拉法求解 y'(t) = -y(t) 的例子：
由于这个方程的导数为负，意味着该函数是一个指数函数，所以 y(t) = exp(-t) 是它的一个解。为了验证前向欧拉法的准确性，我们分别取 h = 0.1 和 h = 0.01，即分别以不同的步长计算函数值估计值。例如，在 h = 0.1 的情况下，我们从 0 开始计算 y(0) 的估计值：
y1 = y0 + h * f(t0, y0) = y0 - 0.1 * y0 = 0.9
然后，再从 t = 0.1 开始计算 y(0.1) 的估计值：
y2 = y1 + h * f(t1, y1) = y1 - 0.1 * y1 = 0.81
以此类推，得到一组数值解 {0.9，0.81，0.729...}。同样的，可以利用 h = 0.01 计算得到一组更为精确的数值解 {0.9901，0.980297，0.970593...}。

显然，随着 h 的减小，数值解精度也会提高，但是计算复杂度也会提高。因此，在实际应用中需要综合权衡，选择适当的步长来对微分方程进行数值解求解。

2）Backward Euler method:

y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n)

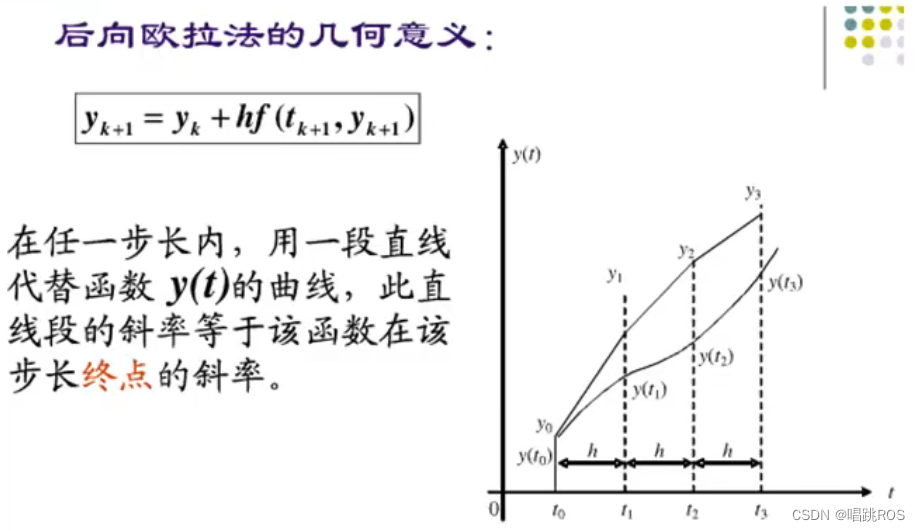
3）Trapezoidal method:

y(n) = y(n-1) + K*[t(n)-t(n-1)]*[u(n)+u(n-1)]/2

离散时间积分模块：

**Integration Forward Euler Method适用于逼近连续函数在一定时间间隔内的积分值。**具体来说，它将函数在积分区间内进行离散化采样，将时间轴离散化为时间步数，并以前向欧拉法逼近积分值。其计算方式是按一定时间间隔递归计算，并将每次的小积分值相加以求得总积分值。Integration Forward Euler Method通常用于计算无法直接求解积分的微分方程问题，以及求解复杂的积分表达式。

**Accumulation Forward Euler Method适用于逼近连续变化的信号在一定时间间隔内的累积和。**具体来说，它将信号在时间轴上进行离散化采样，并使用前向欧拉法逼近信号的积分或累积和。其计算方式是在每个时间步长上逼近积累值，并将采样值和时间步长的乘积相加得到当前的积累值。Accumulation Forward Euler Method通常用于计算信号的平均值、变化速率、能量或功率等。

因此，Integration Forward Euler Method和Accumulation Forward Euler Method的区别在于它们逼近的对象不同，一个是函数的积分值，一个是信号的积分或累积值；它们的计算方式也有所不同，因为其逼近的对象不同，所涉及的离散化采样和时间步长也不相同。

例子：

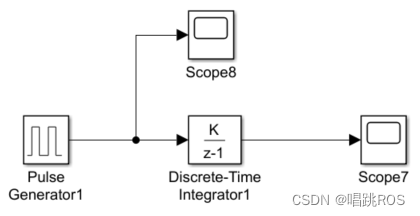
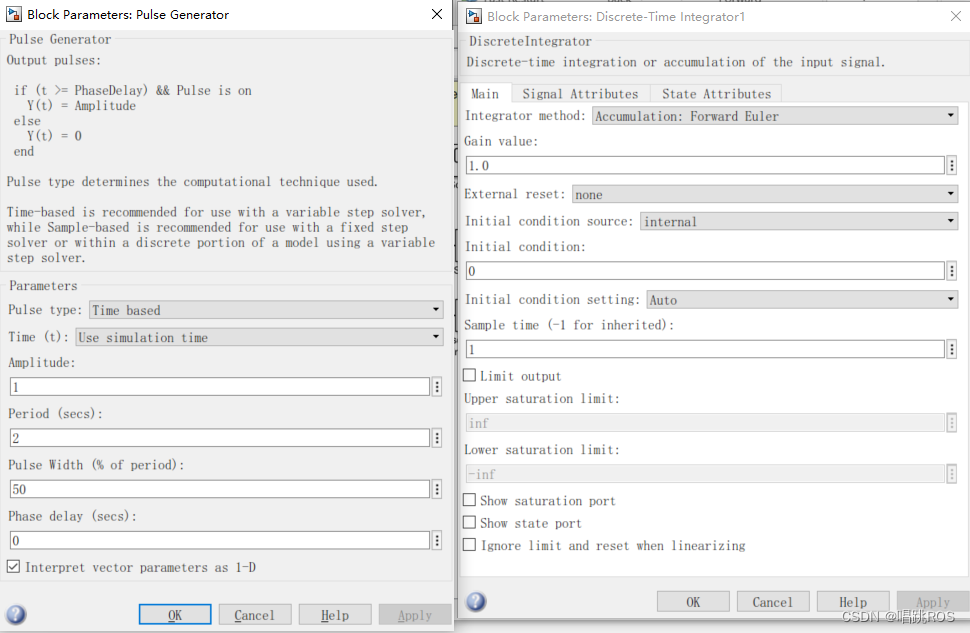
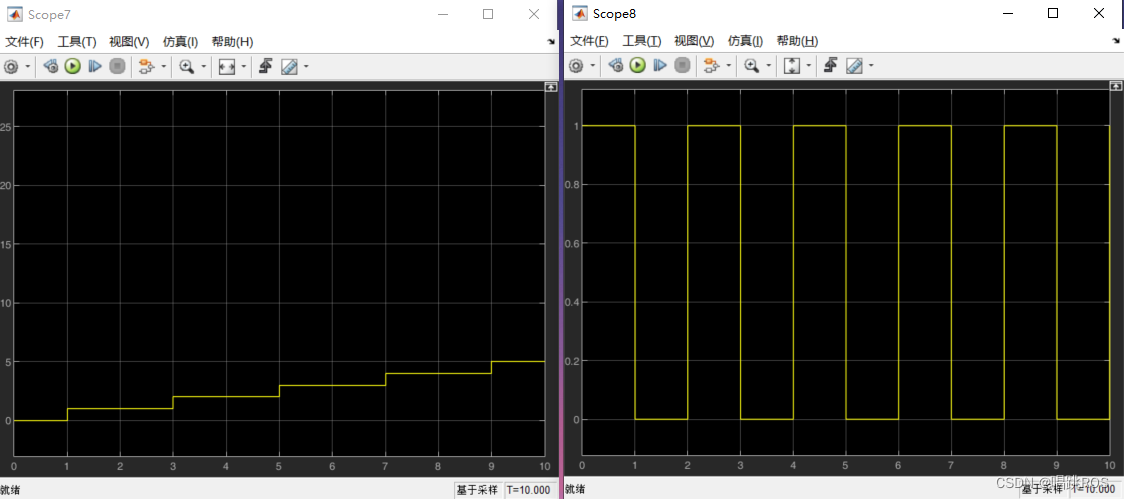
在使用Discrete-Time Integrator时，需要指定其样本时间（sample time）。**如果将样本时间设置为-1，则模块可能会认为该模块不需要进行采样，即不需要进行积分操作。**因此，如果想使用Discrete-Time Integrator进行积分计算，需要正确设置样本时间，以保证结果的正确性和稳定性。

2.12 数据类型转换模块

Input Data Types: single | double | half | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | Boolean | fixed point | enumerated

Output Data Types: single | double | half | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | Boolean | fixed point | enumerated

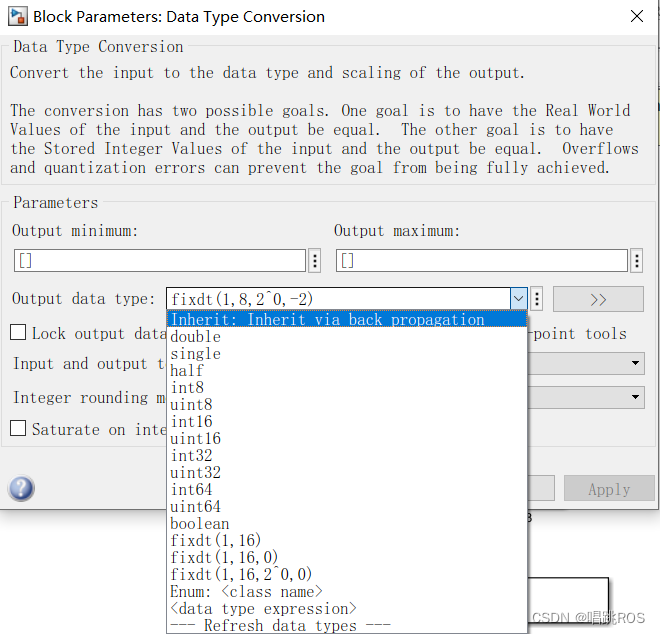
fixdt有三种形式：fixdt(A,B)，fixdt(A,B,C)，fixdt(A,B,D,E)

Input and Output to have equal有两个选择：Real World Value(RWV)和Stored Integer(SI)

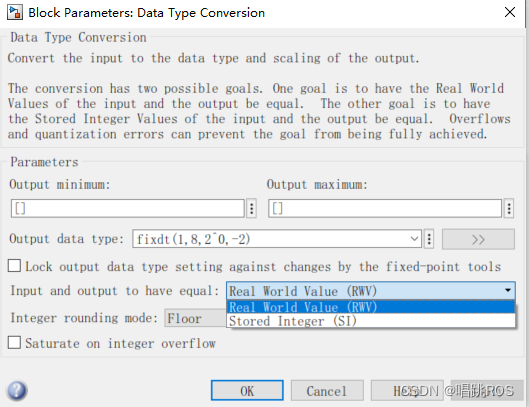
Integer rounding mode

下面详细解释一下这7种整数舍入模式的含义和应用场景。

1. Ceiling：向正无穷取整。例如，对于小数2.1，使用Ceiling模式取整后得到整数3；对于小数-2.1，使用Ceiling模式取整后得到整数-2。在金融计算中，Ceiling模式常用于计算利息和税收等问题。
2. Convergent：根据当前值的奇偶性，向最接近的偶数取整。例如，对于小数2.5，使用Convergent模式取整后得到整数2；对于小数3.5，使用Convergent模式取整后得到整数4。在统计学和信号处理中，Convergent模式常用于对数据进行平滑处理。
3. Floor：向负无穷取整。例如，对于小数2.1，使用Floor模式取整后得到整数2；对于小数-2.1，使用Floor模式取整后得到整数-3。在计算几何和计算机图形学中，Floor模式常用于计算点的坐标。
4. Nearest：四舍五入。例如，对于小数2.4，使用Nearest模式取整后得到整数2；对于小数2.6，使用Nearest模式取整后得到整数3。在科学计算和工程应用中，Nearest模式是最常用的整数舍入模式之一。
5. Round：四舍五入。与Nearest模式相同，Round模式也是四舍五入模式。如果出现平局，则将正数向正无穷大舍入，将负数向负无穷大舍入。
6. Simplest：自动选择最优的舍入模式。Simplest模式会根据当前的计算场景自动选择最优的舍入模式，以提高计算效率。
7. Zero：向零取整。相当于正值用地板模式，负值用天花板模式。从绝对值上看，直接抹掉小数部分。例如，对于小数2.1，使用Zero模式取整后得到整数2；对于小数-2.1，使用Zero模式取整后得到整数-2。

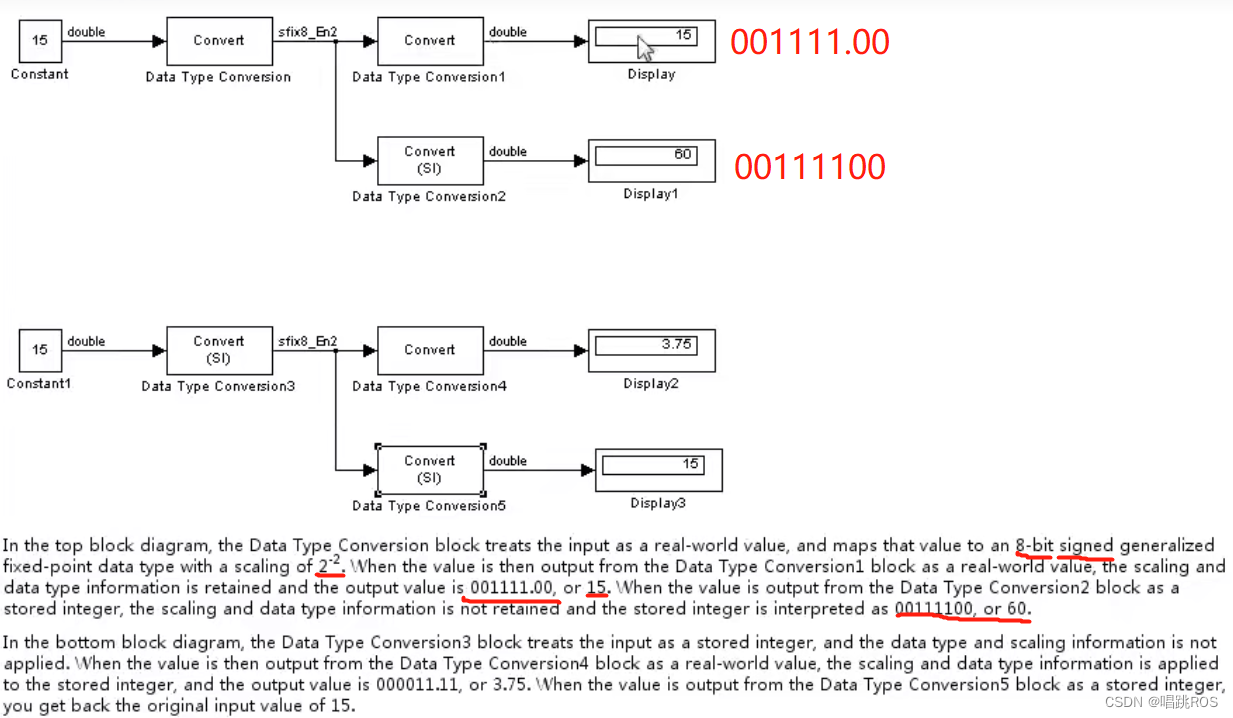
例子：