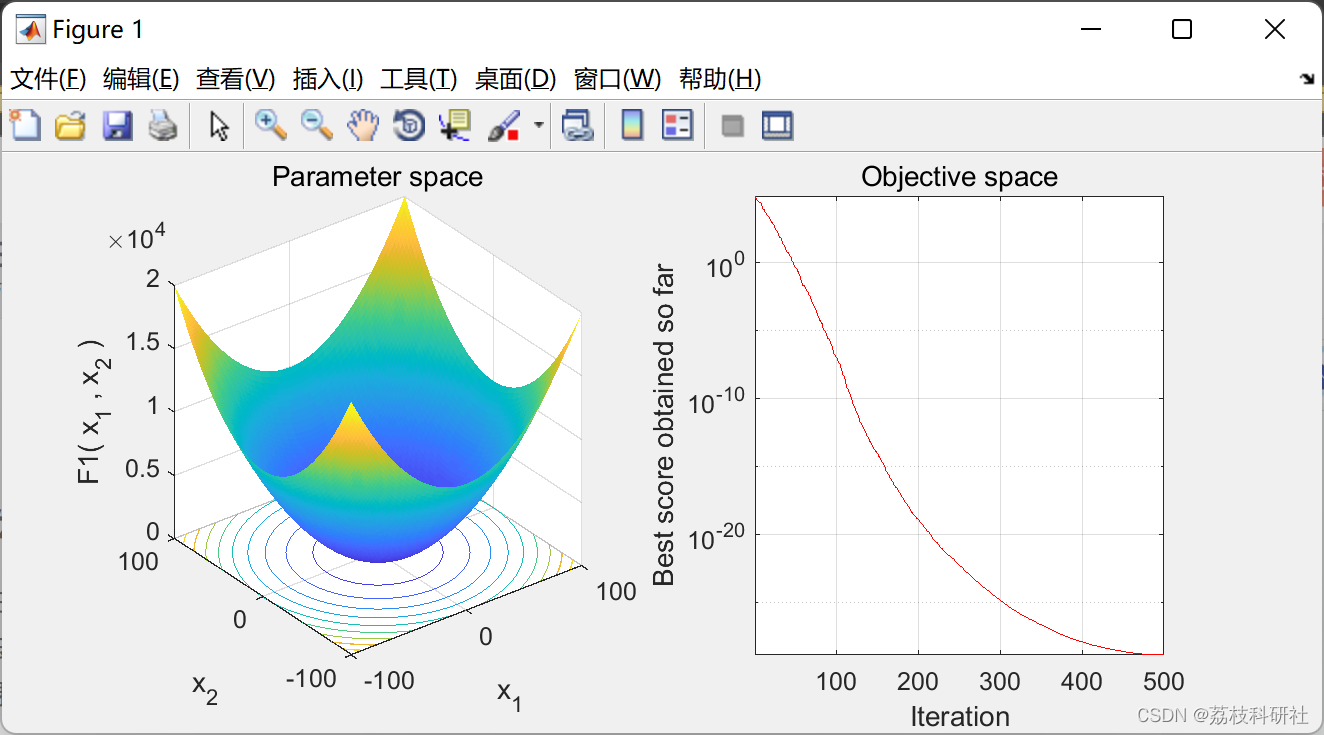
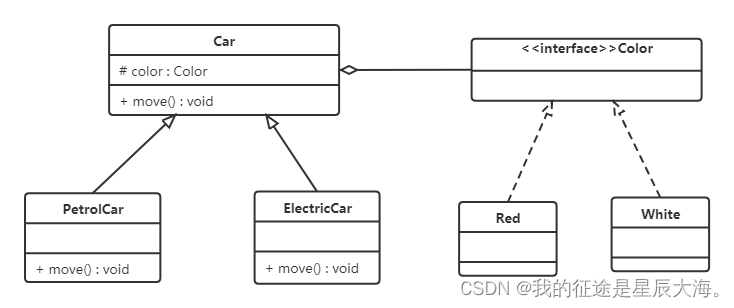
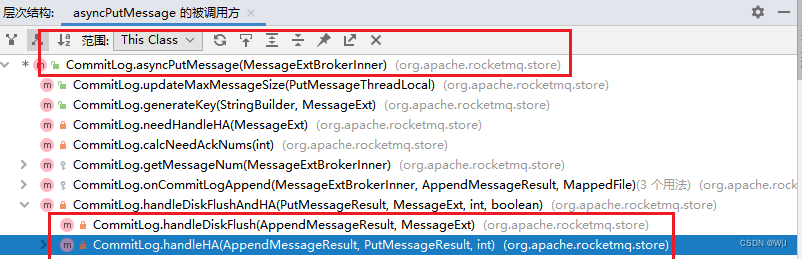
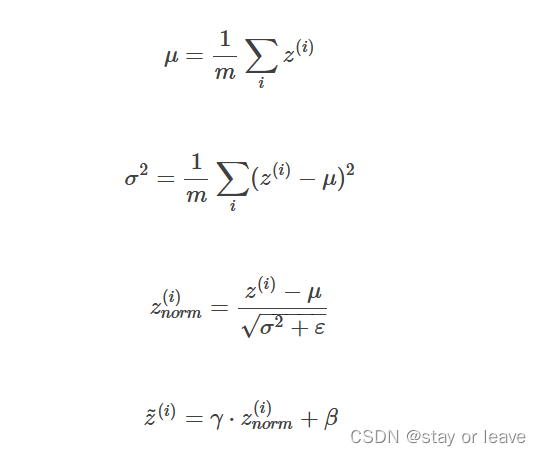超参数的设置：

超参数之间也有重要性差异。通常来说，学习因子α是最重要的超参数，也是需要重点调试的超参数。动量梯度下降因子β、各隐藏层神经元个数#hidden units和mini-batch size的重要性仅次于α。然后就是神经网络层数#layers和学习因子下降参数learning rate decay。最后，Adam算法的三个参数β1,β2,ε一般常设置为0.9，0.999和10−8，不需要反复调试。当然，这里超参数重要性的排名并不是绝对的，具体情况，具体分析。

使用适当的尺度来选择超参数：

均匀随机采样：对于超参数#layers和#hidden units，都是正整数，是可以进行均匀随机采样的，即超参数每次变化的尺度都是一致的（如每次变化为1，犹如一个刻度尺一样，刻度是均匀的）。

非均匀随机采样：超参数α，待调范围是[0.0001, 1]。如果使用均匀随机采样，那么有90%的采样点分布在[0.1, 1]之间，只有10%分布在[0.0001, 0.1]之间。这在实际应用中是不太好的，因为最佳的α值可能主要分布在[0.0001, 0.1]之间，而[0.1, 1]范围内α值效果并不好。因此我们更关注的是区间[0.0001, 0.1]，应该在这个区间内细分更多刻度。

通常的做法是将linear scale转换为log scale，将均匀尺度转化为非均匀尺度，然后再在log scale下进行均匀采样。这样，[0.0001, 0.001]，[0.001, 0.01]，[0.01, 0.1]，[0.1, 1]各个区间内随机采样的超参数个数基本一致，也就扩大了之前[0.0001, 0.1]区间内采样值个数。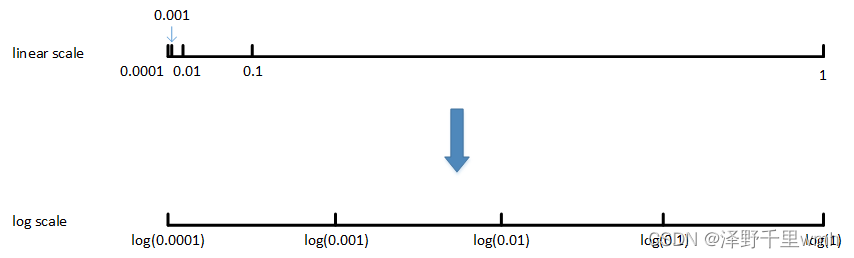

一般解法是，如果线性区间为[a, b]，令m=log(a)，n=log(b)，则对应的log区间为[m,n]。对log区间的[m,n]进行随机均匀采样，然后得到的采样值r，最后反推到线性区间，即10r。10r就是最终采样的超参数。相应的Python语句为：

m = np.log10(a)
n = np.log10(b)
r = np.random.rand()
r = m + (n-m)*r
r = np.power(10,r)

 除了α之外，动量梯度因子β也是一样，在超参数调试的时候也需要进行非均匀采样。一般β的取值范围在[0.9, 0.999]之间，那么1−β的取值范围就在[0.001, 0.1]之间。那么直接对1−β在[0.001, 0.1]区间内进行log变换即可。

批量归一化：

但是，大部分情况下并不希望所有的z(i)均值都为0，方差都为1，也不太合理。通常需要对z(i)进行进一步处理：

 

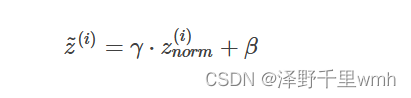
 将批量标准化嵌入神经网络中的流程：

 

测试时的批量标准化：

训练过程中，Batch Norm是对单个mini-batch进行操作的，但在测试过程中，如果是单个样本，该如何使用Batch Norm进行处理呢？

首先，回顾一下训练过程中Batch Norm的主要过程：