如上文所说，JKind 使用了多个并行引擎，协调它们来证明需要检验属性。本文主要介绍 bounded model checking (BMC) 有界模型检验。其中会涉及到有关JKind的 K-induction （k归纳引擎）和 SMT求解机。
本来这些文章就是单纯就是自己的记录，能帮到别人更好，但是写的过程中由于自己的实验过程中的思想不能完整地保留下来，本来理解的东西，很难讲出来，但内容大概是理解的，导致了文章内容目前有些意识流。自己也不是很想写了，哎 归根结底就是菜。未来继续努力吧。
JKind - An infinite-state model checker for safety properties in Lustre

Ⅰ、背景概述

model checking

模型检验以状态来模拟系统，自动检测系统的模拟运行是否满足某些期望的规范。但这其中存在着状态爆炸问题（state-explosion problem）。 模型检验首先需要给定一个系统和我们需要验证的属性，第一步将系统抽象成一个变迁系统，其后 model checking 算法会探索这个系统的每一个状态，来验证系统是否满足这个性质。而对于建模的结构就会很大，就会产生状态爆炸问题。

BMC

而 有界模型检验(BMC) 则可以通过设置界限阈值k，来有效地克服状态爆炸问题。自1999年问世以来，其有两个主要的优势：其优势之一BMC问题编码成 SAT 实例，充分利用 SAT工具进行求解 ，使验证变量数提升一个数量级以上；另一优势是BMC的求解过程向着不满足命题的方向发展，有利于得到长度最短、最简明的反例。（这一点也在JKind发表的会议论文中提到。）

在 Handbook of Model Checking 中有关 SAT 的章节中提到了BMC。在有界模型检验中，对于给定的步长 k，变迁系统和需要验证的属性被联合展开以获得一个公式，如果该属性存在长度为 k 的反例，则该公式为可满足的。 然后将公式传递给高效的SAT求解器。 即可得出其中的反例。也是由于BMC的特性，在JKind中，该引擎只用于验证那些无效的属性。

SMT

接下来再介绍可满足性模理论（Satisfiability Modulo Theory，SMT）。其是SAT问题扩展而来的，SAT问题为一个CNF是否为可满足的，而SMT则是决定一个数理逻辑公式是否为可满足的。其将可满足性问题推广到了实数，整数和各种包含了数据结构的复杂公式。在使用SMT时，我们可以假定存在一个SMT求解器。其输入为一个在某些特定理论片段下的一阶逻辑公式（SMT公式），最终输出该公式的可满足性。

JKind就使用SMT求解机来完成属性的验证和证伪。其求解机默认为 SMTInterpol，但也可选择 Z3, Yices 1, Yices 2, CVC4, and MathSA。我的个人学习是JKind的默认项，因为Java以及将其包含到了库中，学习起来较为简单吧，其他的求解机作者也进行了额外编写。

K-induction

最后需要提一点的是 k-Induction（k 归纳） engine。对于了解 K归纳，我们先复习数学归纳法。 其步骤如下。简单的例子有等差数列求和公式。其实普通数学归纳法是归纳原理的特殊情况。具体在下文中说明。

1. 证明当n= 1时命题成立。
2. 假设n=m时命题成立，那么可以推导出在n=m+1时命题也成立。（m代表任意自然数）
   $$\begin{array}{l}\exists n_0\in {\mathbb{Z}}^{+}.P\left(n_0\right)(1)basecase\\ \forall n_1\in {\mathbb{Z}}^{+}.P\left(n_1\right)\Rightarrow P\left(n_1+1\right)(2)stepcase\\ \Downarrow \\ \forall n\in {\mathbb{Z}}^{+}.n\ge n_0\Rightarrow P(n)\end{array}$$

Ⅱ、理论知识

有关BMC的理论知识，我的理解是集合某位知乎大哥的文章 程序验证（7）- 有界程序验证 和各种网络资源以及 《Handbook of Model Checking》 了解的。特别是这位大佬的专栏，我个人觉得对于程序验证初学者是非常友好的了，其尽量将难度控制再本科生阶段，文章质量也很高，有兴趣的大家去看一下。

Sexp

S表达式，这一部分在最开始写的时候忘了，一看代码想起来了，这部分也比较重要。但是不想去加内容，感兴趣地结合代码与维基百科了解一下。

下近似和上近似（Under- and Over-approximation）

1. 下近似思想用于于证明属性 P 对集合 S 中的某些元素不成立，即证伪。相比于上近似思想，下近似思想更加简单和容易理解。由于 S 集合难以准确表达,那我们就取S中容易表达的子集 S^’ 进行分析。此时，如果 P 对于S’ 中的某些玩素不成立。显然， S’中的元素也是S中的元素。于是,我们在集合S上证伪了属性P。此可见，下近似思想非常朴素，但却也行之有效。

2. 倘若我们希望证明某个性质P在某个集合S上成立，即 P 对 S 中的所有元素都成立: $$\forall xx\in S\Rightarrow P(x)$$而集合S的准确表达可能会很难获得。举例来说， 集合 S 表示某个程序运行过程中，访问数组a的下标变量i的取值集合(访问形式为a[i] ) ;而属性P则表示该程序运行时对数组a的访问不会发生越界(Buffer Overflow/Underflow)，即$$P\triangleq 0\le i<a.\text{ length. }$$如果程序逻辑比较复杂,尤其在循环中变量i取值变化无常时,我们将很难获得集合S的准确表示。这将导致我们难以直接证明属性 P 在集合 S 上成立。
   因此，对于这种情况，我们可以换种思路,试图寻找一个便于表达的集合S’ ，使得S’是S的超集(Superset)，即 S ⊆ S ′ 。同时，我们能证明属性P在S’上是成立的。
   那么, 我们就间接地证明了P在S上成立。这个思想比较简单，也很容易证明其正确性。假设P在S’ 上成立,且 S ∈ S’ ,那么对于每一 个S中的元素x,都有x在S’中,所以P(x )成立。 从而我们可以推导出P(x)在S.上也成立。

有界模型检验(BMC)

有界程序检验（Bounded Model Checking）是一种自动化能力极强的验证算法。 其是一种将验证问题转化为一阶逻辑公式求解的朴素方法。它依赖于下近似思想，对于程序中执行次数未定的循环（无界循环，Unbounded Loop，指不能从代码中轻易得出其执行次数的循环），尝试将其展开固定次数进行分析。
对于一个带有无界循环的程序而言，在它实际的执行路径集合中，循环可能执行 {0, 1 , 2 , 3 , … n } 次（记为集合 S）。在对其应用有界程序验证时，假定将循环展开 K次，那么实际上只取了循环执行**{0, 1 , 2 , 3 , … K }**次的路径（记为集合 S’ ）进行分析。 这显然有 S’ 是 S 的真子集 ，所以有界程序验证是一种下近似验证算法。

现在以一个实际的例子，（该示例来自于多伦多大学2018年的课件SAT and Model Checking）来看BMC算法。
给予了一个变迁系统M，时序逻辑公式 f 和一个用户所给出的步长 k 。现在构造一个命题逻辑公式 Ω(k)，其为可满足的 当且仅当 f 沿长度为k的路径有效。

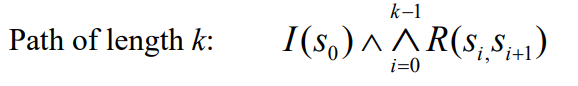
系统的状态在 k 的步长内就可以构造出如上图所示的形式。其中S₀为系统的初始状态，R 代表了转换关系，系统的状态从S_i 可以转换成 S_i+1 。

如果需要验证的 f 为 f = EF p（存在一条路径未来会使得 p 成立） 并且 k = 2。问题就变成了存在一条路径使得未来存在 p。那么 Ω 就变成了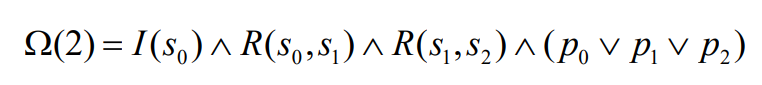
如果 f = AG p，表示 p 在沿着长度为k的任何路径的每个状态下都必须成立。我们通过一个简单的数理逻辑变换即可得到。f 表示了p总是成立，那么 Ω 的非则表示 如果k可达，则成立。变换后得到如下式子。
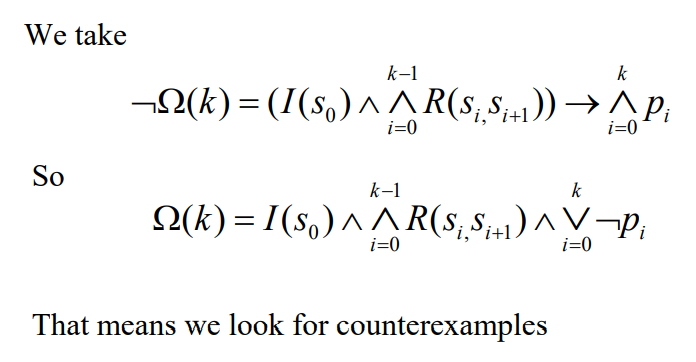由此可以看出，使用BMC可以证伪某个属性来进行系统的安全性检验。至此 BMC 就转化为了一个 SAT问题。

SMT

有了SAT之后，为了求解更大范围的公式，而不仅仅是CNF，就将程序其转化成一阶逻辑公式，再进行求解。JKind的默认求解机为 SMTInterpol。大致内容上文已经说过了，如果细说，这部分也较为赋值，因此不进行赘述。

K-induction

首先用自然数（ 包括了0 ）考虑以下标准的归纳原理：当 P（0）成立时，对于任意的n来说，P（n）成立，则P（n+1）成立，则推导出对于任意的 n 来说，P（n）成立。这就是上文提到的标准的数学归纳法。为 k=1 时的k 归纳法的特殊情况。

而当我们使用 2 - induction 来证明 ∀n P(n) 时，如下所示

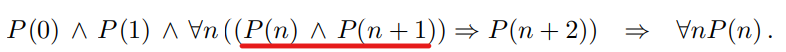
综上所述，K-induction 的归纳公式如下：感觉莫名喜感

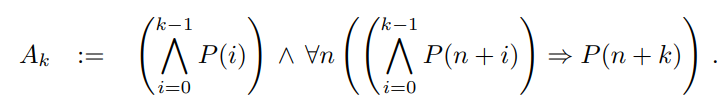
接下来说明 K-induction 是否比 标准的数学规范更好。答案纯粹是务实的：Ak 在实践中可能比 A1 更容易证明：Ak 的第二个合取里的蕴涵，有一个随着 k 增加而变得更强的前提，所以我们有更多的工作要做。 相反，结果 P(n + k) 始终是需要证明的 P 的单个实例。
Ak 的第一个合取，其基本情况，也随着 k 的增加而变得更强，因此需要“更多的证据”，但一事实无关紧要，因为谓词 P 的参数是常数。（以上内容翻译自The k-Induction Principle）

根据以上的内容，将BMC 和 K-induction结合起来看，我们就需要完成如下的证明。我们使用 LP（n）表示需要证明的属性。证明的目标为∀n ≥0 LP（n）。如果使用 k归纳法 ，则我们根据上述的 A_k得出需要证明的两个公式。

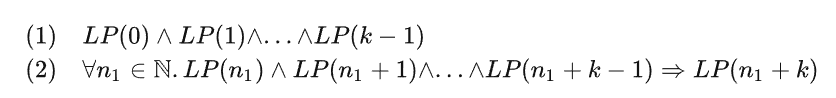
后续步骤看这么大佬的文章吧，因为我真的不行了。程序验证（8）- k归纳法，我将上诉内容用简短，但不一明了的话概括一下：为了证明（1）式，我们需要将程序展开k-1次即可，倘若展开发现了程序中的错误，由于有界程序验证是下近似算法，这代表程序本身存在一条真实的错误路径，直接返回该错误路径即可。 而倘若 k - 1 次展开没有发现错误，那么我们完成了对Base Case的证明，可以继续证明后续的Step Case，使用不变式（注意JKind的引擎结构图，其余的引擎都会向 K-induction 传入不变量）继续对程序进行展开即可。

Ⅲ、JKind中的使用

测试文件

为了更好地理解单个引擎的作业，我将其他引擎进行了禁用，只看 JKind 中 BMC 的运行过程。注意由于BMC只能证伪属性，那些有限的属性其实无法正常运行结束的。如 array.lus 文件中的 ok1 是会导致JKind运行超时的。实验过程中主要使用了 farmer.lus 进行测试。其就是一个简单的狼羊菜渡河问题。
经过上面的解释，对 BMC 验证的过程有了了解之后，看文件内需要验证的属性 prop。关键点在于其中的 not，该属性的含义为 （谁都没有被吃 且 所以东西完成过河 ）的 非。该属性明显是错误的，因为狼羊菜问题是有解的。
对于JKind的命令代码如下所示：

-jkind -no_inv_gen -no_k_induction -pdr_max 0 testing/farmer.lus

引擎输入

书接JKind入门（一），完成文件的输入后，Translate 将源代码通过内联变成了 model checker 所阅读的代码，也就是展开。如下图所示：wolf的值等于boat节点的第一次（下标为0）调用的输出 result；其输入choice 和 object 分别为 main节点的输入 choice 和 1。（这个 1 是因为该段程序涉及到了自定义的枚举数据类型，输入的Wolf 在枚举数据类型的下标为1 ）

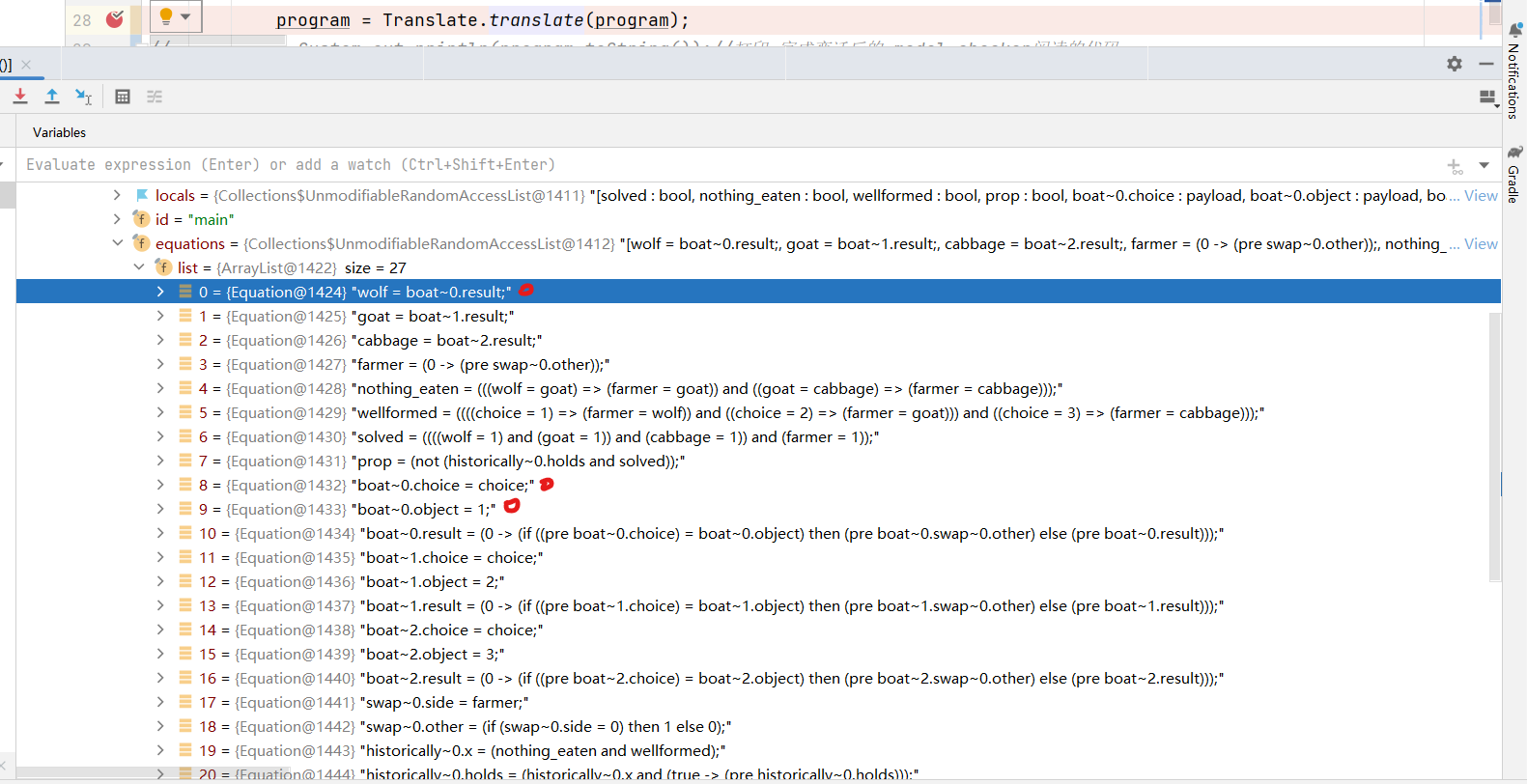
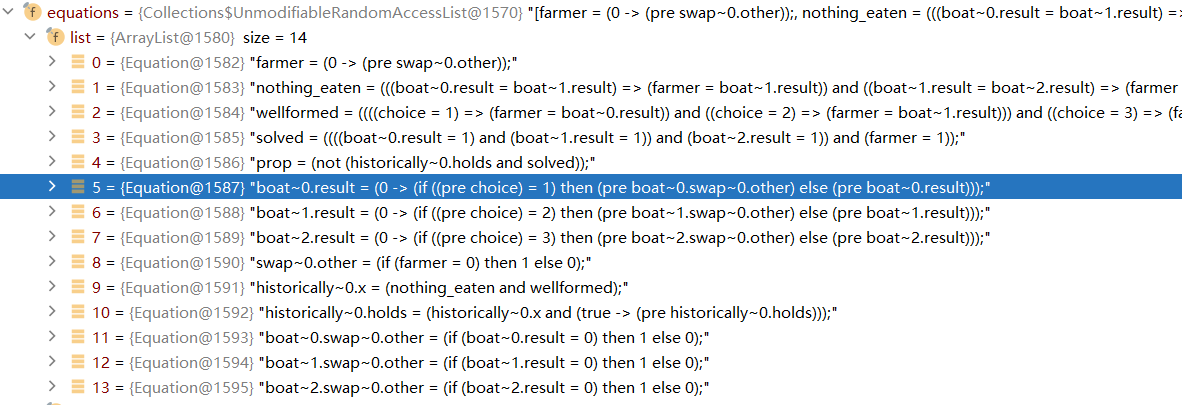
其他同理。之后使用 Specification 生成依赖映射，在使用getAnalysisSpec 完成对于分析代码的精简，除去了简单表达式。(常量表达式 以及 id表达式)如图，此时等式减少到了14条。这14条等式也就是BMC处理的内容。

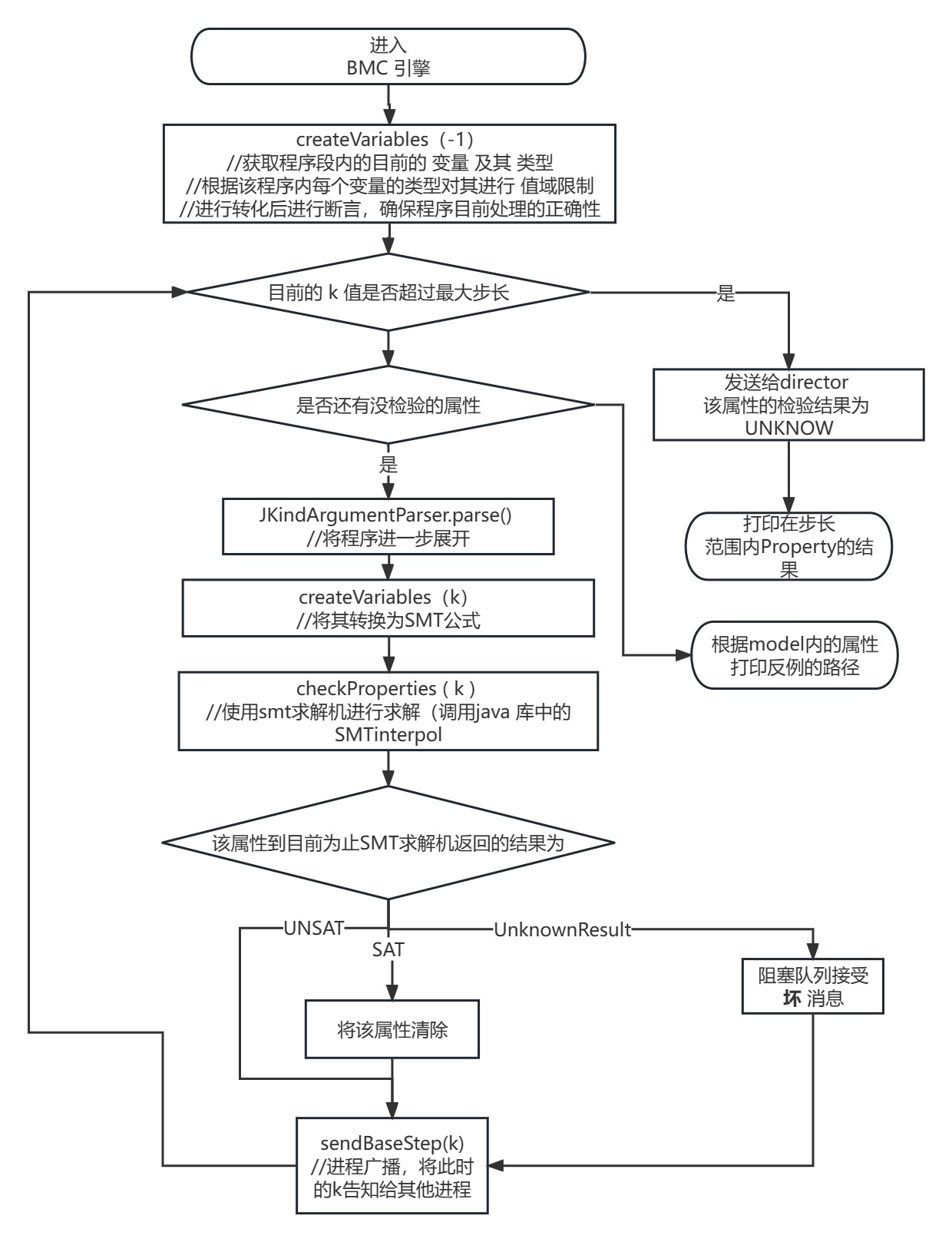
引擎流程图

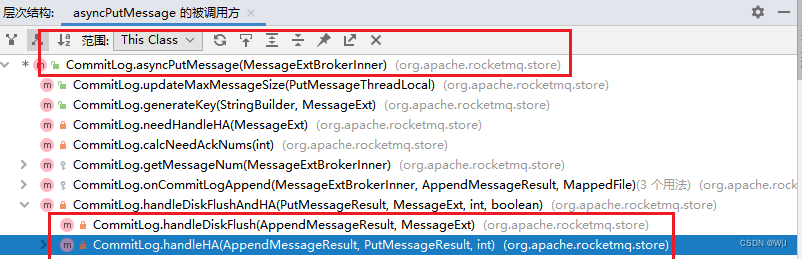
引擎的执行过程如下所示，其中拥有大量的 assert 语句，保证了程序的正确执行。由于过程中涉及的类过多，过于复杂，便在流程图中仅涉及到了方法名。在实验过程中，通过debug模式进入了SMTinterpol的库文件中，我的Java版本为11 ，其底层就是SAT，而且算法方面是DPLL，个人以为会是其升级版的的CDCL，当时更新库文件的时候，该算法认可度还没有那么高？无所谓了。对于JKind来说，由于BMC是K-induction的base case，且k-induction本身也可以验证属性，两者应该就是JKind的核心了，其余引擎加快了JKind处理效率。

之后个人最感兴趣的就是PDR引擎了，回去会浅浅地研究一下。同样，如果本文出现了某些错误，或者理解性的问题，希望各位可以dd我，指正我。有相关研究兴趣的朋友也欢迎来找我玩。
最后 wish u all the best.

运行结果

参考文献

1. S表达式 维基百科
2. SMT 维基百科
3. 程序验证（7）- 有界程序验证
4. 程序验证（8）- k归纳法
5. SAT and Model Checking 多伦多大学
6. The k-Induction Principle 西北大学
7. The JKIND Model Checker
8. 有界模型检验综述[J]. 电脑知识与技术, 2017(12X):2.
9. Clarke, E.M., Henzinger, Th.A., Veith, H., Bloem, R. (Eds.). Handbook of Model Checking. 2018.