【声明】以下内容参考了代码随想录，不用作商业用途~
先来看一个场景：有N件物品，背包最大的重量为W，第i件物品的重量为weight[i]，得到的价值为value[i]，每件物品只用一次（即不能重复放进背包），求怎么装，背包内物体的价值总和是最大的。

像上面这样的问题，其实就是经典的01背包问题，那01背包问题
【解法分析】
这里我们需要构造一个二维数组，二维数组的数据结构如下所示：

这个数组乍一看还是有点云里雾里，其实这里就是用一个二维数组去遍历所有的情况，每个空格表示当前情况下的最大的价值总和，比如dp[i][j]表示当前背包的最大容量为j，里面可放的物品为0-i；

那么接下来我们来推导dp[i][j]，我们一般都希望通过上一个状态去推导现在的状态，但是在二维数组中上一个状态有两个方向，比如dp[i-1][j]和dp[i-1][j-weight],其实写到这里很多人都无法理解为啥突然就是这样子的（尤其逻辑性很强的同学(狗头）），下面具体分析一下，为什么是这样，我的推荐是先记住，然后通过下面的分析知道为什么就可以，自己从0到1推真的很难。

• 由dp[i-1][j]推出，根据上面的描述,dp[i-1][j]表示背包容量为i,里面不放物品i的最大价值，说明此时背包容量利用已经最大化了，加不了其他的物品了，所以dp[i][j]就是dp[i-1][j]；
• 由dp[i-1][j-weight]推出，此时背包容量已经利用最大化，那么dp[i][j]背包容量多了一个物品i的重量，可以放下物品i，所以此时物品的最大价值为dp[i-1][j-weight]+value[i];

因此，我们可以得到递推公式：
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight]+value[i]

接下来，我们需要初始化dp数组，如果背包容量为0，那么背包里面价值肯定也是为0；如下所示：

然后就是遍历，具体细节还是推荐大家去看代码随想录的解析。
下面是一个使用01背包的例题：

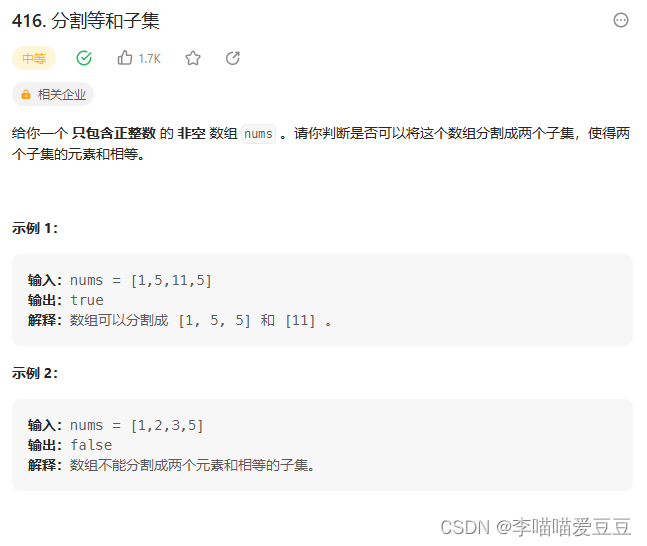
只有确定了如下四点，才能把01背包问题套到本题上来。

• 背包的体积为sum / 2
• 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
• 背包如何正好装满，说明找到了总和为 sum / 2 的子集。
• 背包中每一个元素是不可重复放入。

以上分析完，我们就可以套用01背包，来解决这个问题了。

/**
 * @param {number[]} nums
 * @return {boolean}
 */
var canPartition = function(nums) {
    var sum=0;
    var dp=Array(20001).fill(0);
    for(var i=0;i<nums.length;i++){
        sum=sum+nums[i];
    }
    if(sum%2==1)return false;
    var target=sum/2;
    for(var i=0;i<nums.length;i++){
        for(var j=target;j>=nums[i];j--){
            dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
        }
    }
    if(dp[target]==target)return true;
    return false;

};