目录

118. 杨辉三角 Pascals Triangle  🌟

119. 杨辉三角 II Pascals Triangle II  🌟

120. 三角形最小路径和 Triangle  🌟🌟

🌟 每日一练刷题专栏 🌟

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏

---

118. 杨辉三角 Pascals Triangle

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

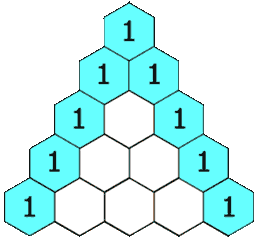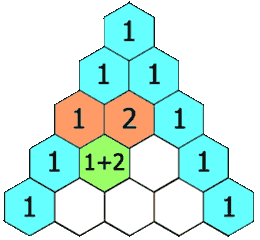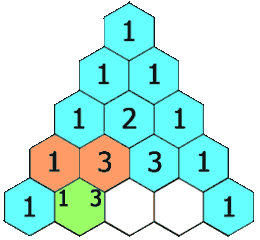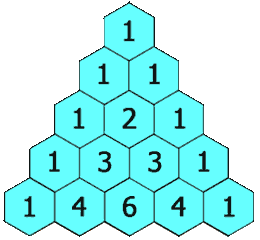
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

• 1 <= numRows <= 30

代码1： 枚举

package main

import "fmt"

func generate(numRows int) [][]int {
	res := make([][]int, numRows)
	for i := range res {
		res[i] = make([]int, i+1)
		res[i][0], res[i][i] = 1, 1
		for j := 1; j < i; j++ {
			res[i][j] = res[i-1][j-1] + res[i-1][j]
		}
	}
	return res
}

func main() {
	for _, i := range []int{5, 1} {
		fmt.Println(generate(i))
	}
}

输出：

[[1] [1 1] [1 2 1] [1 3 3 1] [1 4 6 4 1]]
[[1]]

代码2： 递归

package main

import "fmt"

func generate(numRows int) [][]int {
	res := [][]int{}
	helper(numRows, &res)
	return res
}

func helper(n int, res *[][]int) {
	if n == 0 {
		return
	}
	helper(n-1, res)
	row := make([]int, n)
	row[0], row[n-1] = 1, 1
	for i := 1; i < n-1; i++ {
		row[i] = (*res)[n-2][i-1] + (*res)[n-2][i]
	}
	*res = append(*res, row)
}

func main() {
	for _, i := range []int{5, 1} {
		fmt.Println(generate(i))
	}
}

---

119. 杨辉三角 II Pascals Triangle II

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

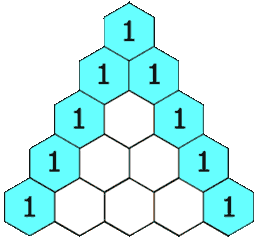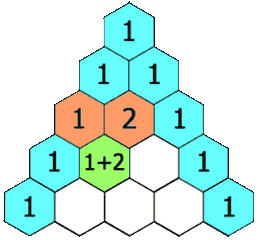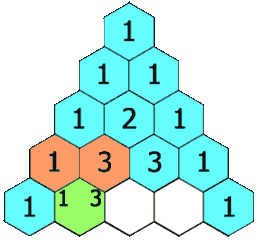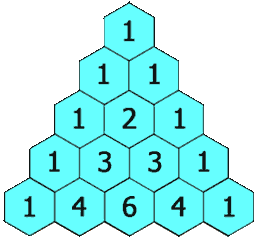
示例 1:

输入: rowIndex = 3
输出: [1,3,3,1]

示例 2:

输入: rowIndex = 0
输出: [1]

示例 3:

输入: rowIndex = 1
输出: [1,1]

提示:

• 0 <= rowIndex <= 33

进阶：

你可以优化你的算法到 O(rowIndex) 空间复杂度吗？

代码1： 枚举

package main

import "fmt"

func getRow(rowIndex int) []int {
	res := make([]int, rowIndex+1)
	res[0] = 1
	for i := 1; i <= rowIndex; i++ {
		for j := i; j > 0; j-- {
			res[j] += res[j-1]
		}
	}
	return res
}

func main() {
	for _, i := range []int{3, 0, 2} {
		fmt.Println(getRow(i))
	}
}

输出：

[1 3 3 1]
[1]
[1 2 1]

代码2：递归

package main

import "fmt"

func getRow(rowIndex int) []int {
	if rowIndex == 0 {
		return []int{1}
	}
	prev := getRow(rowIndex - 1)
	res := make([]int, rowIndex+1)
	res[0], res[rowIndex] = 1, 1
	for i := 1; i < rowIndex; i++ {
		res[i] = prev[i-1] + prev[i]
	}
	return res
}

func main() {
	for _, i := range []int{3, 0, 2} {
		fmt.Println(getRow(i))
	}
}

代码3：组合公式

package main

import "fmt"

func getRow(rowIndex int) []int {
	res := make([]int, rowIndex+1)
	res[0] = 1
	for i := 1; i <= rowIndex; i++ {
		res[i] = res[i-1] * (rowIndex - i + 1) / i
	}
	return res
}

func main() {
	for _, i := range []int{3, 0, 2} {
		fmt.Println(getRow(i))
	}
}

---

120. 三角形最小路径和 Triangle

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

提示：

• 1 <= triangle.length <= 200
• triangle[0].length == 1
• triangle[i].length == triangle[i - 1].length + 1
• -10^4 <= triangle[i][j] <= 10^4

进阶：

• 你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题吗？

代码1： 动态规划

package main

import "fmt"

func minimumTotal(triangle [][]int) int {
	n := len(triangle)
	dp := make([][]int, n)
	for i := range dp {
		dp[i] = make([]int, i+1)
	}
	dp[0][0] = triangle[0][0]
	for i := 1; i < n; i++ {
		dp[i][0] = dp[i-1][0] + triangle[i][0]
		for j := 1; j < i; j++ {
			dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]
		}
		dp[i][i] = dp[i-1][i-1] + triangle[i][i]
	}
	res := dp[n-1][0]
	for i := 1; i < n; i++ {
		res = min(res, dp[n-1][i])
	}
	return res
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func main() {
	triangle := [][]int{{2}, {3, 4}, {6, 5, 7}, {4, 1, 8, 3}}
	fmt.Println(minimumTotal(triangle))
}

输出：

11

代码2： 动态规划（优化）

package main

import "fmt"

func minimumTotal(triangle [][]int) int {
	n := len(triangle)
	dp := make([]int, n)
	dp[0] = triangle[0][0]
	for i := 1; i < n; i++ {
		dp[i] = dp[i-1] + triangle[i][i]
		for j := i - 1; j > 0; j-- {
			dp[j] = min(dp[j-1], dp[j]) + triangle[i][j]
		}
		dp[0] += triangle[i][0]
	}
	res := dp[0]
	for i := 1; i < n; i++ {
		res = min(res, dp[i])
	}
	return res
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func main() {
	triangle := [][]int{{2}, {3, 4}, {6, 5, 7}, {4, 1, 8, 3}}
	fmt.Println(minimumTotal(triangle))
}

代码3： 递归 DFS

package main

import "fmt"

func minimumTotal(triangle [][]int) int {
	n := len(triangle)
	return dfs(triangle, 0, 0, n)
}

func dfs(triangle [][]int, i, j, n int) int {
	if i == n-1 {
		return triangle[i][j]
	}
	left := dfs(triangle, i+1, j, n)
	right := dfs(triangle, i+1, j+1, n)
	return min(left, right) + triangle[i][j]
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func main() {
	triangle := [][]int{{2}, {3, 4}, {6, 5, 7}, {4, 1, 8, 3}}
	fmt.Println(minimumTotal(triangle))
}

---

🌟 每日一练刷题专栏 🌟

✨ 持续，努力奋斗做强刷题搬运工！

👍 点赞，你的认可是我坚持的动力！ 

🌟 收藏，你的青睐是我努力的方向！ 

✎ 评论，你的意见是我进步的财富！  

☸ 主页：https://hannyang.blog.csdn.net/ 

	Golang每日一练 专栏
	Python每日一练 专栏
	C/C++每日一练 专栏
	Java每日一练 专栏