七大排序之插入排序

---

前言

博主个人社区：开发与算法学习社区

博主个人主页：Killing Vibe的博客

欢迎大家加入，一起交流学习~~

一、直接插入排序

插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

1.1 算法图解

其实就是打牌码牌的过程。

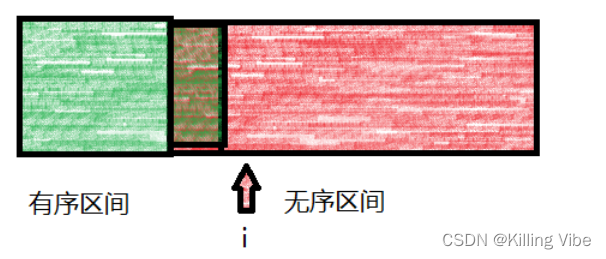
• 将待排序的集合看做两部分，已排序的区间(0…i) ; 待排序的区间[i…n);
• 每次选择无序区间的第一个元素插入到有序区间的合适位置，直到整个数组有序。

初始数据越接近有序，效率越高，经常作为高阶排序算法优化手段。

代码如下：

    public static void insertionSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            // 已排序区间[0...1)
            // 待排序区间[i ..n)
            // 选择无序区间的第一个元素，不断向前看
            // 注意看内层循环的终止条件 j >= 1而不是 j >= 0 ?
            // 因为此时arr[j] 不断向前看一个元素  j - 1 要合法 j - 1 >= 0
            for (int j = i; j >= 1 && arr[j] < arr[j - 1]; j--) {
                swap(arr,j,j - 1);
//                // 边界
//                if (arr[j] > arr[j - 1]) {
//                    // arr[i] 恰好是有序区间的后一个元素，无序区间的第一个元素
//                    // 当前无序区间的第一个元素 > 有序区间最后一个元素
//                    break;
//                }else {
//                    swap(arr,j,j - 1);
//                }
            }
        }
    }

注意事项：

当arr[i] > arr[i-1] 时 ，说明此时arr[i] 大于有序区间的所有元素！！！

直接跳过内层循环，外层i++

举个栗子：

算法走到一半时：

• 有序区间： [1,2,3,4,5]
• 无序区间：[6,9,8,7,2,10]

1.因为 6 > 5 , 所以直接跳过内层循环了，然后 i++

2.有序区间变成 [1,2,3,4,5,6]

3.只有当arr [i] < arr[i - 1] 的时候才需要移动元素

4.从当前元素不断向前看，往前交换 swap（arr,j,j-1）

5.一直碰到arr[j] > arr[j - 1] 就停止，即插入到了合适的位置。

1.2 算法稳定性

当arr[j] >= arr[j - 1] 不会交换其顺序，循环退出了。

所以插入排序是一个稳定性的算法。

1.3 插入排序和选择排序相比到底优在哪？

1.和选择排序最大的区别：

当已经排序的集合的最后元素 < 当前无序区间的第一个元素，内层循环可以直接退出，大大降低了时间。

2.极端情况：

若待排序的数组就是一个完全升序数组，插入排序就会进化为O(n) = > 内层循环一次也不走，最好情况时间复杂度

二、折半插入排序

选择无序区间的第一个元素插入到”有序区间“的位置时，优化他的插入位置的查找次数。

也就是有序区间的查找用二分查找。

代码如下：

    public static void insertionSortBS(int[] arr) {
        // 有序区间[0..i)
        // 无序区间[i..n)
        for (int i = 0; i < arr.length; i++) {
            int val = arr[i];
            // 有序区间[left...right)
            int left = 0;
            int right = i;
            while (left < right) {
                int mid = (left + right) / 2;
                if (val < arr[mid]) {
                    right = mid;
                }else {
                    // val >= arr[mid]
                    left = mid + 1;
                }
            }
            // 搬移[left..i)的元素
            for (int j = i; j > left ; j--) {
                arr[j] = arr[j - 1];
            }
            // left就是待插入的位置
            arr[left] = val;
        }
    }

举个栗子：

当算法进行到一半时：

绿色框框已经是有序数组，红色是待排序数组。

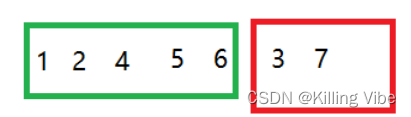
对绿色框框里面的元素用二分查找的方法：

left = 0 ； right = i； mid = (left + right) / 2；

• 第一轮开始 l = 0，r=5，mid = 2 ，比较当前元素和arr[mid]的大小关系，3<4, 就把right = mid = 2，往mid的左区间【1 2】来查找
• 第二轮开始 l = 0 , r = 2, mid = 1 , 重复上述操作，3 > arr[mid] 也就是2，所以 l = mid+1 = 2
• 第三轮开始 l= 2,r = 2,此时 l > = r 循环终止，此时需要插入的位置就是 l
• 此时只需要将[l…i)的元素往后搬移即可

总结

以上就是插入排序的图解和代码，有什么疑问可以私信博主~有帮助的话可以关注博主后续更新。