平行光阴影

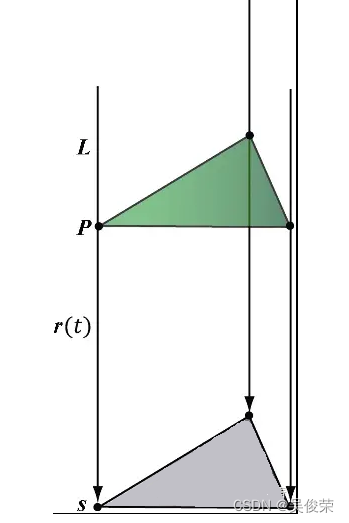
在这里插入图片描述
图展示了由平行光源经物体所投射岀的阴影。给定方向为L的平行光源，并用r（t）=p + tL来表示途经顶点p的光线。光线r （t）与阴影平面(n,d）的交点为S。以此光源射出的光线照射到物体的各个顶点，用这些映射到平面上的交点集合便可以定义几何体所投射出的阴影形状。对于顶点P来说，它的阴影投影可由下列公式求岀:
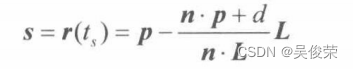
在这里插入图片描述
公式也可以写作矩阵的形式

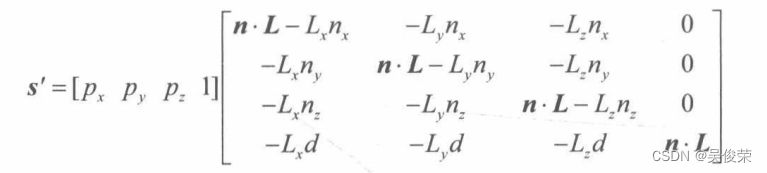
我们称以上的4x4矩阵为方向光阴影矩阵（directional shadow matrix,也译作平行光阴影矩阵），Sdir表示。为了证明此矩阵与公式是等价的，我们用乘法运算加以验证。首先可以看出，此矩阵改变了w分量，即Sw=n·L。这样一来，当执行透视除法时，S中的每个坐标都会除以Si其中 i∈｛1,2, 3｝。在透视除法完成之后，我们有：

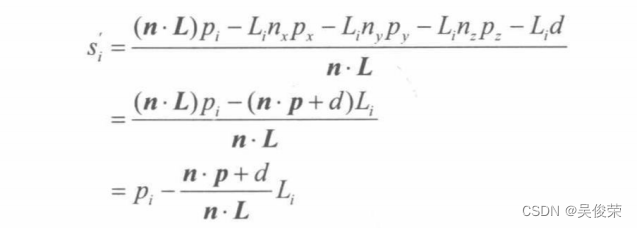
在这里插入图片描述
此结果与公式求出的s中的第i个坐标完全相同，因此s=s’。

为了运用阴影矩阵，我们将它与世界矩阵组合在一起。但是，在世界变换之后，由于透视除法还没有执行，因而几何体的阴影还未被投射到阴影平面上。此时便出现了一个问题：若Sw=n·L<0,则w坐标将变为负值。在透视投影的处理过程中，我们一般将 z 坐标复制到 w 坐标，若 w 坐标为负值则表明此点位于视锥体之外而应将其裁剪掉(裁剪操作在透视除法之前的齐次空间内执行)。这对于平面阴影来讲是个大问题，因为除了计算透视除法之外，我们还要用 w 坐标来实现阴影效果。图就展示了这样一种n·L<0却存在阴影的情况，但此时这个阴影却无法显示出来。
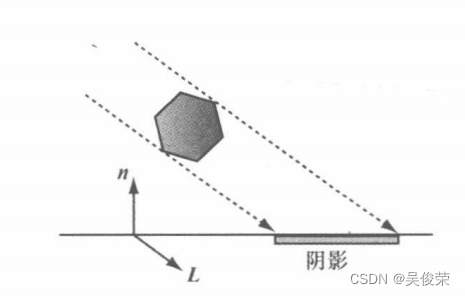
在这里插入图片描述

为了纠正这个问题，我们用指向无穷远处光源的方向向量L1 = -L来取代光线方向向量L。可以看岀， r（t）=p + tL与r（t）=p + tL1定义的是相同的3D直线，且该直线与平面之间的交点也是一致的(利用不同的交点参数值ts来弥补L1与L之间的符号差异)。因此使用L1 = -L 会得到与L相同的计算结果，但是前者会保证n·L>0,以此来绕开w坐标为负值的这个坑。

点光阴影

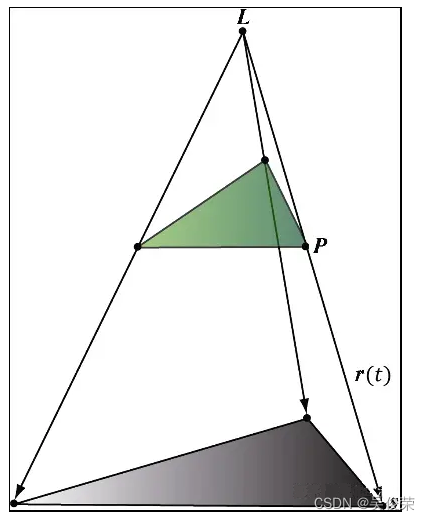
在这里插入图片描述
图展示了位于点 L 处的点光源所投射出的物体阴影。从点光源发出的途经任意顶点p的光线可由r(t) = p + t(p - L)来表示。光线r(t)与阴影平面(n,d)的交点为s。以此光源发出的光线经过物体的每个顶点，这映射在平面的交点集合便定义了几何体所投射出的阴影形状。对于顶点 p 而言，其阴影投影可以表示为：
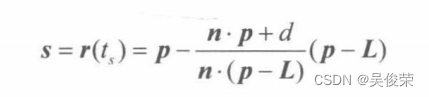
在这里插入图片描述
公式也可以写作矩阵方程：

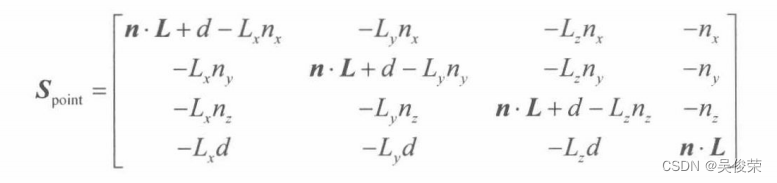
为了证明此矩阵等价于公式我们就以上面同样的办法，用矩阵进行乘法运算。观察到最后一列中并没有0项，则有：
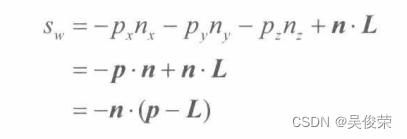
在这里插入图片描述
这就是公式中分母部分的相反数，我们可以通过将分子与分母同时乘以T,使二者一致。

对于点光与平行光而言，L 充当着不同的角色。在使用点光时，L 定义了点光源的位置。在使用平行光时，我们却用 L 来定义指向无穷远处光源的方向向量（即与平行光光线传播方向相反的向量）。

通用阴影矩阵

我们可通过齐次坐标创建出一个能同时应用于点光与方向光的通用阴影矩阵。

1.如果Lw=0 ,则 L 表示指向无穷远处光源的方向向量（即与平行光光线传播方向相反的向量）。
2.如果如果Lw=1，则 L 表示点光的位置。

接下来，我们用下列阴影矩阵（shadow matrix）来表示由顶点p到其投影s的变换：
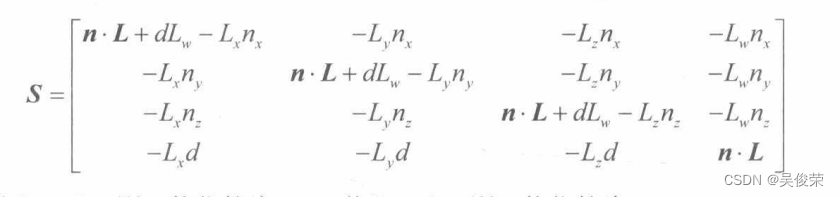
在这里插入图片描述
DirectX的数学提供了以下函数，用以构建在特定平面内投射阴影所用的相应阴影矩阵，若w = 0 表示平行光，而w=l则表示点光：
inline XMMATRIX XM_CALLCONV XMMatrixShadow（
FXMVECTOR ShadowPlane,
FXMVECTOR LightPosition）;

使用模板缓冲区防止双重混合

将物体的几何形状投射到平面而形成阴影时，可能（实际上也经常岀现）会有两个甚至更多的平面阴影三角形相互重叠。若此时用透明度这一混合技术来渲染阴影，则这些三角形的重叠部分会混合多次, 使之看起来更暗。

1.首先，保证参与渲染阴影的模板缓冲区中的阴影范围像素都已被清理为0。
2.设置模板测试，使之仅接受模板缓冲区中元素为0的像素。如果通过模板测试，则将相应模板缓冲区值增为1。

在第一次渲染阴影像素时，由于模板缓冲区元素为0,因而模板测试会成功。渲染该像素的同时，我们也会将对应的模板缓冲区元素增加为1。这样一来，如果试图覆写已被渲染过的区域，则模板测试会失败。这将防止同一像素被绘制多次，继而阻止双重混合的发生。

编写阴影部分的代码

auto shadowMat = std::make_unique<Material>();
	shadowMat->Name = "shadowMat";
	shadowMat->MatCBIndex = 4;
	shadowMat->DiffuseSrvHeapIndex = 3;
	shadowMat->DiffuseAlbedo = XMFLOAT4(0.0f, 0.0f, 0.0f, 0.5f);
	shadowMat->FresnelR0 = XMFLOAT3(0.001f, 0.001f, 0.001f);
	shadowMat->Roughness = 0.0f;

	//为了防止双重混合，我们用下列的深度/模板状态来设置PSO:
	//以下列深度/模板状态来防止双重混合的发生
	// 我们要用透明度绘制阴影，所以基于透明度描述
	D3D12_DEPTH_STENCIL_DESC shadowDSS;
	shadowDSS.DepthEnable = true;
	shadowDSS.DepthWriteMask = D3D12_DEPTH_WRITE_MASK_ALL;
	shadowDSS.DepthFunc = D3D12_COMPARISON_FUNC_LESS;
	shadowDSS.StencilEnable = true;
	shadowDSS.StencilReadMask = 0xff;
	shadowDSS.StencilWriteMask = 0xff;

	shadowDSS.FrontFace.StencilFailOp = D3D12_STENCIL_OP_KEEP;
	shadowDSS.FrontFace.StencilDepthFailOp = D3D12_STENCIL_OP_KEEP;
	shadowDSS.FrontFace.StencilPassOp = D3D12_STENCIL_OP_INCR;
	shadowDSS.FrontFace.StencilFunc = D3D12_COMPARISON_FUNC_EQUAL;

	// 我们不渲染背面多边形，所以这些设置无关紧要。
	shadowDSS.BackFace.StencilFailOp = D3D12_STENCIL_OP_KEEP;
	shadowDSS.BackFace.StencilDepthFailOp = D3D12_STENCIL_OP_KEEP;
	shadowDSS.BackFace.StencilPassOp = D3D12_STENCIL_OP_INCR;
	shadowDSS.BackFace.StencilFunc = D3D12_COMPARISON_FUNC_EQUAL;

	D3D12_GRAPHICS_PIPELINE_STATE_DESC shadowPsoDesc = transparentPsoDesc;
	shadowPsoDesc.DepthStencilState = shadowDSS;
	ThrowIfFailed(md3dDevice->CreateGraphicsPipelineState(&shadowPsoDesc, IID_PPV_ARGS(&mPSOs["shadow"])));

//绘制阴影
mCommandList->OMSetStencilRef(0);
	mCommandList->SetPipelineState(mPSOs["shadow"].Get());
	DrawRenderItems(mCommandList.Get(), mRitemLayer[(int)RenderLayer::Shadow]);

    //更新阴影的世界矩阵
	XMVECTOR shadowPlane = XMVectorSet(0.0f, 1.0f, 0.0f, 0.0f); // xz plane
	XMVECTOR toMainLight = -XMLoadFloat3(&mMainPassCB.Lights[0].Direction);
	XMMATRIX S = XMMatrixShadow(shadowPlane, toMainLight);
	XMMATRIX shadowOffsetY = XMMatrixTranslation(0.0f, 0.001f, 0.0f);
	XMStoreFloat4x4(&mShadowedSkullRitem->World, skullWorld * S * shadowOffsetY);