基本概念
什么是快速幂呢?个人理解,就是更快速的计算幂运算。
比如计算a^b
刚学这个算法的时候我也很疑惑,幂运算不是有现成的公式么,直接pow(a,b)不就好了吗?
后来才明白,pow(a,b)的时间复杂度是O(b),即每次乘b,都得再运算一次。
如果b的值很大,那么代码的运行时间会很长,很多题目会疯狂时间超限。
而快速幂算法的时间复杂度是O(logb),可以有效减少运行计算机计算的次数。
例子
下面我举个简单小的例子:
计算2^32(a=2,b=32)
2*2=2^2;
2^2 *2^2 =2^4;
2^4 *2^4 =2^8;
2^8 *2^8 =2^16;
2^16 *2^16 =2^32;
时间复杂度优化为O(log32)
可以认为,这个算法基于倍增原理,与其每次逐个乘,不如每次将a的值翻倍
当b是2的整数幂时,计算很简单,可是若b不是2的整数幂时该怎么办呢?
下面再举一个小例子:
计算5^105
这个时候,虽然105不是2的幂,但是我们可以把它写成2的幂的和。
105,1+8+32+64=2^0 + 2^3,+ 2^5+ 2^6
这个算法的关键就是我们如何把b分解为2的幂之和
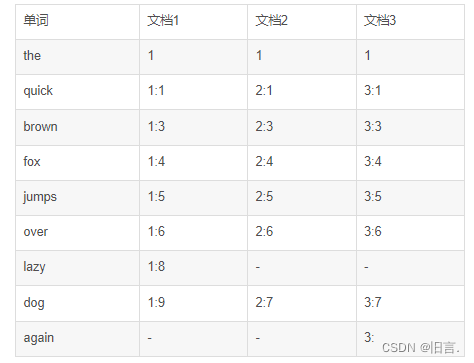
下面列一个表,从二进制的角度来分解这个问题
首先,105,1, 8,32,64这5个数的二进制表示:
很明显,105每个二进制位中的1和下面的数的二进制位中的1是一一对应的
我们通过这种方式,将b分解为2的幂的和
伪代码:
fun(a, b)
sum = 1
while b != 0
if(n % 2 == 1)
sum = sum * a
a = a * a
b = n / 2
从b的初始值开始,对b的每一个二进制位进行遍历,如果该位等于一,则让sum乘以a
下面是快速幂的代码
int quick_mi(int m, int k, int p) {
int res = 1 % p;
int t = m;
while(k) {
if(k & 1) res = res * t % p;
t = t * t % p;
k >>= 1;
}
return res;
} PS:
第一条:
“&”是与运算
n&1 与运算 可以判断n是否为偶数 如果是偶数,n&1返回0;否则返回1,为奇数
第二条:
左移1位相当于乘以2,左移运算符“<<”;
右移1位相当于除以2,右移运算符“>>”;
本题中b>>=1,相当于b=b/2
第三条:
关于取模运算,大家可自行百度
由于时间匆忙,例题改日更新,敬请期待!